Beam Load Calculator
This beam load calculator will help you determine the reactions at the supports of a simply-supported beam due to vertical point loads or forces. In this calculator, we will explore the following:
- What support reaction is;
- How to calculate support reactions in a beam;
- Sample calculation of how to find support reactions; and
- How to calculate beam load capacity using this beam load calculator.
Knowing how to find support reactions is a great place to start when analyzing beams, such as when determining beam deflection. Keep on reading to learn more.
🙋 If you're curious about how to calculate beam deflections, we have our beam deflection calculator you can check out, or our feature-packed wood beam span calculator for in-depth calculation on wood beam design.
What is a support reaction?
According to Newton's third law of motion, every force on an object has an equal and opposite reaction. If you try to push onto something, let's say a wall, it feels like the wall is also pushing back at you. That is exactly the phenomena Newton's third law of motion describes.
In engineering, structural members such as beams and columns interact with each other at the points where they meet. Imagine a beam that is being supported in place by two columns. The beam's weight pushes down on the columns, and because of Newton's third law of motion, we can then also say that the columns exert an equivalent opposite reacting force back on the beam. We call these reacting forces support reactions.
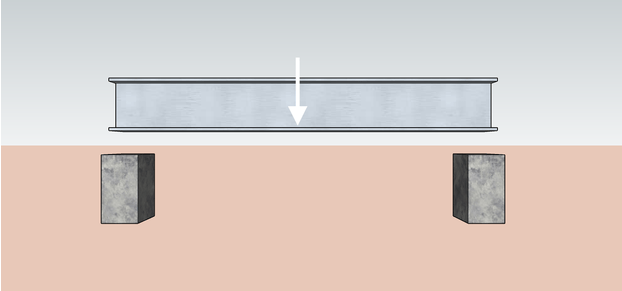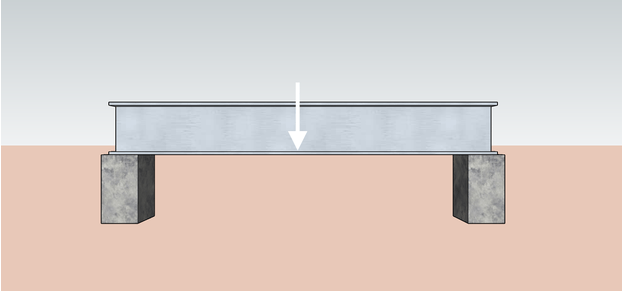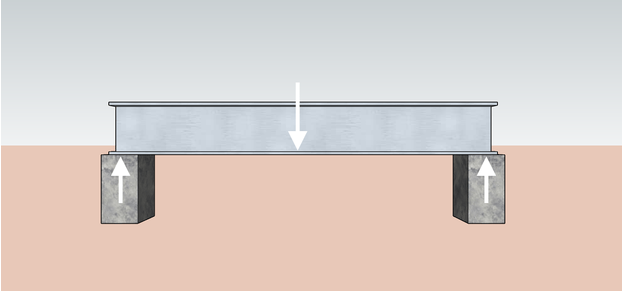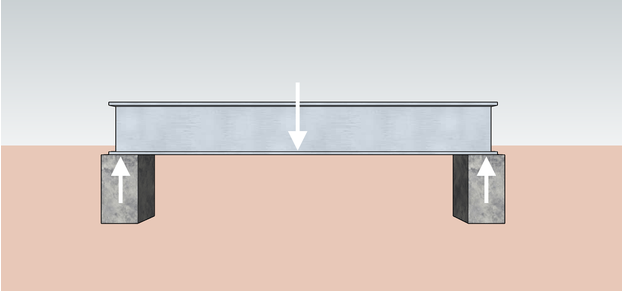
You can imagine a door header as the beam shown above and the two jack studs (the vertical studs where the door header rests) as the two supporting structures of the door header. Learn more about door header sizes by checking out our door header size calculator.
On a simply-supported beam, the support reactions at each end of the beam can either be equal to each other or of different values. Their values depend on the beam's applied loads. If more loads are found at a closer distance to one support, that support-structure experiences more force and therefore experiences a greater reaction.
How to calculate support reactions in a beam
Since support reactions act in the opposite direction as the force, we can say that the whole system is in equilibrium. That means the beam is not moving, and the summation of forces and moments result in zero. By equating the moments due to load to the moments due to support reactions, we can then determine the reactions at the supports.
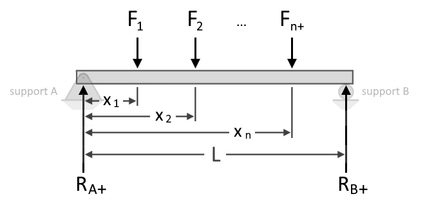
Just like when calculating torque, we can also perform a summation of moments at each supports to solve for the reactions. Below, we express a summation, , of the moments at support A to find the reaction at support B, denoted as , as shown below:
or
where:
- , , , and – The point loads on the beam at distances , , , and , from support A, respectively;
- – Reaction at support B; and
- – Length of the beam between support A and support B.
By rearranging the equation, we can isolate as follows:
Now that we have an expression to find , and since we know that the total applied forces are equal to the reactions' total, we can now also find the reaction at support A, , using the following equations:
Now that we know how to calculate support reactions in beams, let us now consider an example calculation to strengthen our knowledge about it. 🙂
Sample calculation of how to find support reactions
Suppose we have a 4.0-meter long simply-supported beam with an applied 10.0 kilonewtons (kN) point load 2.0 meters from support A and another applied 3.5 kN point load 1.5 meters from support B, as shown below:
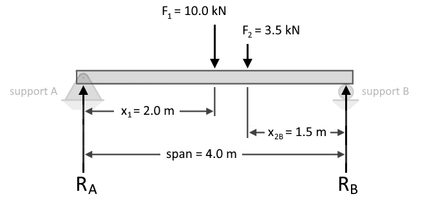
To calculate for , we formulate the equation of moment equilibrium as follows:
By performing a summation of forces, we obtain:
Please note that for this summation, we have considered all downward forces as positive and all upward forces as negative. Based on our calculations above, we have now obtained the reactions at supports A and B to be 6.3125 kN and 7.1875 kN, respectively.
Also, please take note that in this example of how to find support reactions and in the beam load calculator, we assumed that the beam is weightless. However, if the beam's weight is indicated, you can consider the beam's weight as another downward point load at the center, or centroid, of the beam.
Using our beam load calculator
Our calculator is easy and simple to use. All you have to do is input the span of the beam, enter the number of loads on the beam, the magnitude of the point loads, and their distances from support A.
If you want to enter an upward load, simply enter a negative value for the load magnitude. In total, you can input up to 10 point loads in our beam load calculator.
FAQs
What's a simply supported beam?
A simply supported beam is a beam that has two supports located at each end. One support is a pinned support, which allows only one degree of freedom, the rotation around the z-axis (perpendicular to the paper). At the other end, there's a roller support, which enables two degrees of freedom, the horizontal movement along the x-axis and rotation around the perpendicular z-axis.
How do I determine the support reactions on a simply supported beam?
To determine the reactions on a simply supported beam:
-
Draw the beam's free body diagram.
-
Sum the moments at one support, such as pin support A:
Σ(Fi × xi) - RyB × beam_span = 0
Where:
- Fi – Vertical forces;
- xi – Distance between A and the point load; and
- RyB – Vertical reaction at roller support B.
-
To find the vertical reaction at A, RyA, sum the vertical forces:
ΣFy = ΣFi - RyB - RyA = 0.
-
Sum the horizontal forces to find the horizontal reaction at A RxA:
ΣFy = ΣFi - RxA = 0.
What's the importance of calculating the support reactions?
Calculating the support reactions is essential for understanding the internal forces in a beam. In beam design, we need to understand how the internal shear forces and bending moments behave. By knowing how these loads vary along the beam, we can accurately analyze and predict the resulting stresses and deformations, helping us to design beams capable of withstanding these conditions, ensuring structural integrity and safety.
What are the reactions of a 6 m simply supported beam?
For a beam with a uniformly distributed weight load of 5 kN/m, the reactions at A and B are both 15 kN. To calculate this:
-
Draw the beam's free body diagram, including the equivalent point load for the weight.
-
Sum the moments at pin support A to find the vertical reaction at roller support B:
RyB = 30 kN × 3 m/6 m = 15 kN.
-
Sum the vertical forces to find the vertical reaction at A:
RyA = 30 kN - 15 kN = 15 kN.
-
The horizontal reaction at support A, RxA, is zero.
