Pascalsches Dreieck Rechner

Willkommen bei unserem Pascalsches-Dreieck-Rechner. Hier erfährst du, wie du das Pascalsche Dreieck benutzen kannst und warum du es überhaupt benutzen solltest. Keine Sorge, dieses Konzept erfordert keine Flächeninhalt-Formeln oder Einheitsberechnungen, wie bei einem typischen Dreieck. Was ist also das Pascalsche Dreieck? Nun, es ist eine nette Methode, um die Anzahl der Kombinationen zu berechnen und die binomischen Formeln zu visualisieren. Doch bevor wir mit der Beschreibung der Muster des Pascalschen Dreiecks beginnen, wollen wir uns erst einmal mit den Grundlagen beschäftigen.

Das Pascalsche Dreieck ist eine Zahlentabelle in Form eines gleichseitigen Dreiecks, bei der die k-te Zahl in der n-ten Zeile angibt, wie viele Kombinationen ohne Wiederholung 🇺🇸 von k-Elementen es in einem Set von n-Elementen gibt. Sie ist nach dem französischen Mathematiker Blaise Pascal benannt.

(Beachte, dass wir der Konstruktion folgen, dass die oberste Zeile, die mit der einzelnen 1, als Zeile Null gilt , während die erste Zahl in einer Zeile, ebenfalls eine 1, als die nullte Zeile gilt.) Die n-te Zeile zählt also alle möglichen Kombinationen eines Sets mit n Elementen. Egal, ob es sich um Filme für einen Filmmarathon, um europäische Länder, die du diesen Sommer besuchen willst, oder um Zutaten aus deinem Kühlschrank für das morgige Abendessen handelt, diese Aussage über Kombinationen bleibt immer wahr (wir sind uns ziemlich sicher, dass das letzte nicht genau so funktioniert wie das Kochen, aber manche von uns müssen den Mangel an Fähigkeiten mit Kreativität ausgleichen).

Jede Zahl, die in unserem Rechner für das Pascalsche Dreieck angezeigt wird, wird durch die binomischen Formeln angegeben, die dein Mathelehrer ständig erwähnt (der im Binomialverteilung Rechner als nCr bezeichnet wird). Der Name ist nicht so wichtig, aber schauen wir uns mal an, wie die Berechnung aussieht. Wenn wir die Anzahl der Kombinationen von k Elementen aus einem Set mit n Elementen als C(n,k) bezeichnen, dann:

C(n,k) = n! / (k! × (n-k)!).

Das Ausrufezeichen oben steht für die „Fakultät”, definiert als das Produkt aller Zahlen bis einschließlich n, d. h.,

n! = n × (n-1) × (n-2) × ... × 2 × 1.

Angenommen, du bereitest einen Filmmarathon für dich und deinen Partner vor. Du hast eine Liste mit deinen zwanzig Lieblingsfilmen und dein Partner hat dir gesagt, du sollst drei auswählen, die ihm gefallen könnten. Nun, das sind die besten Filme, die es gibt, also wird er natürlich jeden einzelnen mögen. Somit ist es eigentlich egal, welche du auswählst. Auch die Reihenfolge, in der ihr euch die Filme anseht, spielt keine Rolle. Wie viele Möglichkeiten gibt es also?

Die Zahl, die du suchst, ist die dritte Zahl in der zwanzigsten Reihe, 1140. Magie? Nicht ganz, nur Mathematik (aber sind sie denn so unterschiedlich?). Nach unserer Formel entspricht diese Zahl dem Ausdruck C(20,3), der die Anzahl der Dreiergruppen in einem Set mit zwanzig Elementen angibt. Oder, in unserem Fall, die Anzahl der Möglichkeiten, wie wir drei Filme aus einem Stapel von zwanzig auswählen können.

Blaise Pascal konzentrierte sich auf mehrere interessante Eigenschaften des Dreiecks. Tatsächlich war die Anzahl der Kombinationen, die als einzelne Zahlen in aufeinanderfolgenden Zeilen verschlüsselt sind, schon zu seiner Zeit bekannt. Allerdings wird das Dreieck oft mit einer viel einfacheren Regel eingeführt. Beachte, dass, abgesehen von den 1en an den äußersten Enden des Dreiecks, jede der anderen Zahlen die Summe der beiden Zahlen ist, die direkt über ihr stehen.

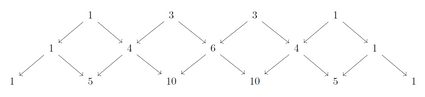
Das ist genau die Beobachtung (oder Eigenschaft, wenn du so willst), die häufig zur Konstruktion des Dreiecks verwendet wird. Mit der Formel des Pascalschen Dreiecks können wir diese Beobachtung beschreiben:

C(n,k) = C(n-1,k-1) + C(n-1,k).

Schau dir vor allem die zweite Zahl von links in jeder Zeile an. Jede dieser Zahlen hat links oben eine Eins und rechts oben die Zeilennummer der vorhergehenden Zeile. Ihre Summe ist also eins plus die Nummer der vorhergehenden Zeile (das ist der Kern unseres Arithmetische Folge Rechners), und das Ergebnis ist die Zeile, in der wir uns befinden.

Ein weiteres interessantes Muster des Pascalschen Dreiecks ist seine Symmetrie. Beachte, dass wir in jeder Zeile wenn wir die aufeinanderfolgenden Zahlen von links lesen, dasselbe erhalten, wie wenn wir sie von rechts lesen. Ist es wieder Magie oder Mathematik? Versuchen wir zu verstehen, was hier passiert.

Laut Definition gibt die Zahl an der k-ten Stelle in der n-ten Zeile an, wie viele Möglichkeiten es gibt, k Elemente aus einem Set von n Elementen auszuwählen. Aber wie wäre es, wenn wir stattdessen auf die Elemente hinweisen würden, die wir nicht ausgewählt haben? Das klingt vielleicht ein bisschen vage, also warum zeigen wir dir nicht ein Beispiel?

Erinnere dich an das Szenario aus [dem zweiten Abschnitt](#wie-benutzt-man-das --pascalsche-preieck), wo wir aus einer Liste von zwanzig Filmen drei auswählen wollten. Aber was ist, wenn es schwierig ist, die drei auszuwählen, die du am liebsten sehen möchtest? Vielleicht ist es einfacher, die Filme, die du nicht sehen willst, einzeln zu streichen? Wenn wir dann siebzehn davon streichen, bleiben uns nur noch drei übrig. Das ist genau das, was wir oben beschrieben haben — wir wählen stattdessen siebzehn aus, die wir uns nicht ansehen möchten. Dies wird mit der Notation von Pascals Dreiecksformel in [dem ersten Abschnitt] (#was-ist-das-pascalsche-dreieck) beschrieben und lautet:

C(n,k) = C(n,n-k),

was für uns bedeutet, dass die Zahl in der k -ten Stelle, wenn man von links zählt, die gleiche ist wie die in der k-ten, wenn man von rechts zählt, für jede Zeile n.

Mathematisch gesehen ist die Antwort auf „Was ist das Pascalsche Dreieck?” genau dies: Binomische Formeln. Keine Sorge, wir sind nicht hier, um mit hochtrabenden Worten und Symbolen zu prahlen, wenn eine einfache Erklärung ausreicht. Wir zeigen dir anhand eines realen Szenarios, wie du diese Frage beantworten kannst, und erklären dir nebenbei, wie du den Pascalschen Dreiecksrechner benutzen kannst.

Angenommen, dein Hund bekommt Welpen und du weißt, dass es sechs sind, aber du kennst ihr Geschlecht nicht. Wenn wir die Welpen in der Reihenfolge nummerieren, in der sie auf die Welt kommen, können wir uns Gedanken über die Wahrscheinlichkeit machen, welches Geschlecht sie haben werden. Sicherlich sind sechs Rüden nicht so wahrscheinlich wie z. B. zwei Rüden und vier Hündinnen. Das liegt daran, dass die beiden Rüden die ersten beiden Welpen sein können, oder die letzten beiden, oder die mittleren beiden, usw. Es gibt also viel mehr Kombinationen, in denen das passieren kann.

Okay, jetzt kommt der knifflige Teil. Wir werden versuchen, dich davon zu überzeugen, dass die Welpen durch (x + y)⁶ beschrieben werden können. Um das zu sehen, verbindest du x mit „Rüde” und y mit „Hündin”. Schau dir jetzt die Erweiterung an:

(x + y)⁶ = (x + y) × (x + y) × ... × (x + y).

Wie entsteht jeder Summand, nachdem wir den obigen Ausdruck ausmultipliziert haben? Nun, er entsteht, indem wir einen der Summanden in jeder der Klammern nehmen, d.h. indem wir entweder x oder y nach der Klammer nehmen. In unserer Übersetzung bedeutet das, dass das Geschlecht jedes der sechs Welpen einzeln bestimmt wird. Das bedeutet, dass jeder Summand der Form x² × y⁴, der dem zweimaligen Ziehen von x aus der Klammer und dem viermaligen Ziehen von y entspricht, einen Wurf mit zwei Rüden und vier Hündinnen ergibt.

Schauen wir uns nun die Erweiterung nach der Multiplikation und der Umformung der ähnlichen Monomere an:

(x + y)⁶ = x⁶ + 6x⁵y + 15x⁴y² + 20x³y³+ 15x²y⁴ + 6xy⁵ + y⁶.

Vergleiche es mit der sechsten Ebene des Pascalschen Dreiecks, die der Pascalsche Dreiecksrechner liefert:

1 6 15 20 15 6 1.

Diese Zahlen entsprechen den Koeffizienten in der obigen Erweiterung. Mit anderen Worten: die sechste (bzw. n-te im Allgemeinen) Ebene des Dreiecks entspricht den Koeffizienten von (x + y)⁶ (bzw.: hoch n) in deren binomischen Formeln. Und wie wir bei unserem Hundeszenario gesehen haben, lässt sich dies auch auf einige reale Probleme übertragen.

Wenn du eine Pascalsche Dreieckszeile berechnen möchtest:

1. Beginne damit, die Spitze des Dreiecks aufzuschreiben: Die nullte Zeile enthält eine einzelne 1.

2. Dann enthält die erste Zeile zwei 1er.

3. Alle anderen Zeilen folgen dem gleichen Prinzip: Schreibe eine 1 am Anfang und am Ende auf. Jede der fehlenden Zahlen ist die Summe der beiden Zahlen, die direkt über ihr stehen (in der vorherigen Zeile).

4. Befolge diese Regeln, bis du die Zeile hast, die du brauchst.

Die Summe der Zahlen in der n-ten Zeile des Pascalschen Dreiecks ist gleich 2ⁿ. Tatsächlich können wir leicht feststellen, dass die nachfolgenden Summen 1, 2, 4, 8, 16 usw. sind. Das folgt aus der Tatsache, dass das Set von n Elementen 2ⁿ Teilmengen hat.

Die siebte Zeile des Pascalschen Dreiecks ist 1 7 21 35 35 21 7 1.

Die zehnte Zeile des Pascalschen Dreiecks ist 1 10 45 120 210 252 210 120 45 10 1.