Calculadora de porcentajes

Esta calculadora de porcentajes es una herramienta que te permite hacer un cálculo sencillo: ¿qué porcentaje de X es Y? La herramienta es bastante sencilla. Todo lo que tienes que hacer es rellenar dos campos, y el tercero se calculará por ti automáticamente. Este método te permitirá responder a la pregunta de cómo hallar el porcentaje de dos números.

Además, nuestra calculadora de porcentajes también te permite realizar el cálculo a la inversa, es decir, cómo hallar el porcentaje de un número. Intenta introducir varios valores en los distintos campos y verás lo rápida y fácil de usar que es esta práctica herramienta. ¿Solo saber cómo obtener un porcentaje de un número no es suficiente para ti? Si buscas cálculos más extensos, pulsa el botón de modo avanzado(advanced-mode) debajo de la calculadora.

Además de ser útil para aprender porcentajes y fracciones 🇺🇸, esta herramienta es útil en muchas situaciones diferentes. ¡Puedes encontrar porcentajes en casi todos los aspectos de tu vida! Cualquiera que haya ido de compras alguna vez, seguro que ha visto decenas de carteles con un gran símbolo de porcentaje que dice “¡descuento!”. Y este es solo uno de los muchos ejemplos de porcentajes. Aparecen con frecuencia, por ejemplo, en finanzas, donde los utilizamos para averiguar el importe del impuesto sobre la renta o sobre las ventas, o en salud para expresar cuál es tu grasa corporal.

Sigue leyendo si quieres aprender cómo hallar un porcentaje de algo, cuál es la fórmula del porcentaje y las aplicaciones de los porcentajes en otros ámbitos de la vida, como la estadística o la física.

El porcentaje es una de las muchas formas de expresar una relación adimensional entre dos números (los otros métodos son las razones o proporciones y las fracciones). Los porcentajes son muy populares porque pueden describir situaciones que implican números grandes (por ejemplo, estimar las posibilidades de ganar la lotería), promedios (por ejemplo, determinar la nota final de tu curso), así como muy pequeños (como la proporción volumétrica de NO₂ en el aire, también expresada frecuentemente en ppm - partes por millón).

Uno por ciento es una centésima. Como símbolo de porcentaje, solemos utilizar % o a veces simplemente decir “por ciento”. Significa que 5 por ciento es lo mismo que 5 %, 0.05, 5/100 o cinco centésimas. Es tan sencillo como eso, y esta calculadora de porcentajes es una herramienta creada para trabajar con fracciones decimales y porcentajes. Si buscas resolver problemas más complicados, averigua cómo calcular el porcentaje de un porcentaje 🇺🇸.

Todo esto está muy bien, pero normalmente no usamos los porcentajes por sí solos. Normalmente, queremos responder a ¿Qué tan grande es un número en comparación a otro número?. Para intentar visualizarlo, imagina que tenemos algo que le gusta a todo el mundo, por ejemplo, un paquete de galletas (o chocolates, lo que prefieras😉). Intentemos encontrar una respuesta a la pregunta ¿cuál es el 40 % de 20? Son 40 centésimas de 20, así que si dividiéramos 20 galletas en 100 partes iguales (¡buena suerte intentándolo!), la suma de 40 de esas partes sería el 40 % de 20 galletas. Hagamos las cuentas: 40/100 × 20 = 8. Un truquito útil: para dividir por 100, basta con desplazar el punto dos espacios a la izquierda. En nuestro cálculo, 40/100 × 20 podría hacerse como (40 × 20)/100 (es lo mismo). 40 × 20 es 800. Moviendo el punto de 800 dos dígitos a la izquierda, obtienes 8.00, y cuando te deshaces de todos los ceros innecesarios, obtienes 8. En nuestra calculadora, introduce 40 y 20 (para que diga “40 % de 20” es 8).

Un porcentaje también es una forma de expresar la relación entre dos números como una fracción de 100. En otras palabras, el porcentaje nos dice cómo es la proporción entre un número y otro. Si sabemos que el número A es el 25 % del número B, sabemos que A es a B como 25 es a 100, o, luego de simplifica, como 1 es a 4, es decir, A es cuatro veces menor que B. Esto es lo que enseña la calculadora de porcentajes: qué es un porcentaje y cómo hallar el porcentaje de dos números.

¿Cómo hallar el porcentaje de algo? Es más fácil explicar qué es el porcentaje con galletas. Supongamos que tenemos un gran cajón con 100 compartimentos (una cuadrícula de 10 x 10). Cada compartimento es una centésima o el 1 % de todo el cajón. Entonces llenamos este cajón con galletas de forma que tengamos exactamente el mismo número de galletas en cada compartimento.

Empecemos por el ejemplo más sencillo con 100 galletas. ¿Cómo obtener el porcentaje de, digamos, cinco galletas? Es fácil: a cada compartimento le corresponde exactamente una galleta. Por tanto, el 1 % de 100 es una galleta, y mientras que el 5 % son cinco galletas.

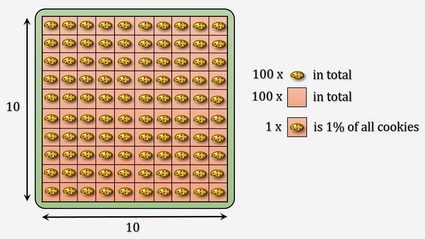
Vamos con algo un poco más difícil y cuatro veces más delicioso: ¡400 galletas! Las dividimos equitativamente, y cada compartimento recibe cuatro galletas. Las galletas parecen más pequeñas, pero en nuestra imaginación son iguales, ¡solo que el cajón es mucho más grande! El 1 % de 400 son 4. ¿Qué te parece el 15 %? Son 15 compartimentos multiplicados por 4 galletas: 60 galletas. Nos empieza a doler un poco el estómago, ¡pero eso nunca nos ha impedido comer más galletas!

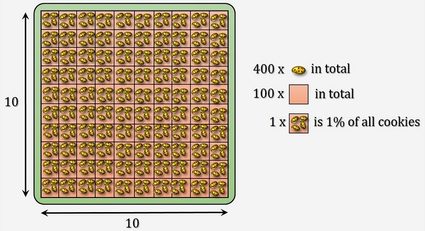
Ahora, algo aún más difícil: 250 galletas. Dividimos las primeras 200 galletas, colocando dos en cada compartimento. Ahora nos quedan 50 galletas que hay que repartir uniformemente, mmm, es media galleta en cada caja. ¿Cómo calcular el porcentaje? Tienes razón: esta vez, el 1 % del número total de 250 galletas es 2.5. ¿Y cuántas tenemos en 15 cajas? 2.5 × 15 o sea 37.5.

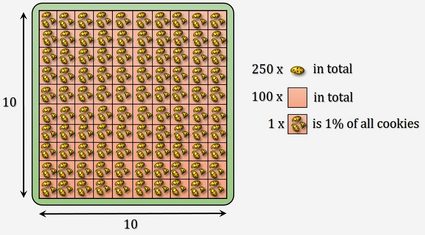
Entonces, ¿para qué sirve el porcentaje? Como hemos escrito antes, un porcentaje es una forma de expresar una razón o proporción. Supongamos que estás haciendo un examen con nota. Si te dijéramos que has obtenido 123 puntos, en realidad no te diría nada. ¿123 sobre qué? Ahora bien, si te dijéramos que has obtenido un 82 %, esta cifra sería más comprensible. Aunque te dijéramos que sacaste 123 puntos sobre 150, sería más difícil intuir lo bien que te ha ido. Una semana antes, hubo otro examen, y obtuviste 195 de 250, es decir, el 78 %. Aunque es difícil comparar 128 de 150 con 195 de 250, es fácil darse cuenta de que una puntuación del 82 % es mejor que una del 78 %. ¿No es verdaderamente útil el signo de porcentaje? ¡Al fin y al cabo, es el porcentaje lo que importa!

¿Y qué pasa con las fracciones decimales y los porcentajes? Los porcentajes se pueden convertir fácilmente en decimales. Solo tienes que dividir el valor del porcentaje por 100, y ya está. 15 % es lo mismo que 0.15. Así que, como hemos visto antes, 0.15 de 250 galletas es treinta y siete y medio.

Los porcentajes son a veces mejores para expresar diversas cantidades que las fracciones decimales en química o física. Por ejemplo, es mucho más cómodo decir que la concentración porcentual de una sustancia concreta es del 15.7 % que afirmar que hay 18.66 gramos de sustancia en 118.66 gramos de disolución. Otro ejemplo es la eficiencia (o su caso especial: la eficiencia de Carnot). ¿Es mejor decir que el motor de un automóvil funciona con una eficiencia del 20 % o que produce una energía de 0.2 kWh a partir de una energía de entrada de 1 kWh? ¿Qué te parece? Estamos seguros de que has aprendido que obtener el porcentaje de un número es una habilidad valiosa.

Aunque ciertamente es rápido e indoloro utilizar nuestra calculadora de porcentajes, no siempre tienes acceso a una computadora o a un teléfono inteligente. Además, es genial poder hacer los cálculos mentalmente. Quizá no tanto como hacer malabares con antorchas encendidas, pero casi.

El porcentaje te dice cómo se relaciona un número A con otro número B. Un ejemplo del mundo real podría ser: hay dos niñas en un grupo de cinco niños. ¿Cuál es el porcentaje de niñas? En otras palabras, queremos saber cuál es la proporción de niñas respecto al total de niños. Es 2 de cada 5, o 2/5. Llamamos numerador al primer número (2) y denominador al segundo número (5) porque se trata de una fracción. Para calcular el porcentaje, multiplica esta fracción por 100 y añade un signo de porcentaje. 100 × numerador / denominador = porcentaje. En nuestro ejemplo, es 100 × 2/5 = 100 × 0.4 = 40. El 40 % del grupo son chicas. Ese es todo el procedimiento de conversión entre fracciones decimales y porcentajes.

¿Tienes problemas para simplificar fracciones? La mejor forma de resolverlo es hallar el MCD (máximo común divisor) del numerador y denominador y dividir ambos por dicho MCD.

Hagamos el camino inverso e intentemos encontrar el numerador. Digamos que sabemos que el 70 % de las frutas de la cesta son manzanas, y que hay 30 frutas en total. Podría ser peor: podrían ser limones. Entonces, ¿cuántas manzanas tenemos? Obtengamos nuestra fórmula del porcentaje: 100 × numerador / denominador = porcentaje. Queremos averiguar el numerador. Movamos todas las demás partes de la ecuación al otro lado. Primero, divide ambos lados por 100 (para deshacerte del 100 de la izquierda) y luego multiplica a ambos lados por el denominador. Esto es lo que obtenemos numerador = porcentaje × denominador / 100. Sustituyamos el porcentaje y el denominador por nuestros valores: numerador = 70 × 30 / 100. Ahora es fácil: numerador = 2100 / 100 = 21, tenemos 21 manzanas. Debería bastar para un almuerzo o para una pelea de comida bastante violenta.

Ahora vamos a resolver un problema con un denominador desconocido. Gastamos el 30 % de nuestro dinero en chicles (nunca hemos dicho que seamos grandes inversores). Compramos 12 chicles a 1 $ cada uno. Así que sabemos que 12 $ eran el 30 por ciento de nuestro presupuesto total. ¿Cuánto dinero teníamos antes de que, casi literalmente, lo echáramos todo a perder? Empecemos con nuestra fórmula 100 × numerador / denominador = porcentaje o 100 × 12 / denominador = 30. Esta vez queremos averiguar el denominador. Multipliquemos ambos lados por el denominador y luego dividámoslo por el porcentaje. Así obtendremos 100 × 12 / 30 = denominador. Y al revés, denominador = 100 × 12 / 30 = 1200 / 30 = 40. Teníamos 40 $, y nos gastamos el 30 %, o sea 12 $, en chicles. Valió totalmente la pena.

Siguiendo con nuestros ejemplos de galletas, vamos a nombrar las tres partes de nuestra ecuación: el porcentaje de galletas (40 %), el total de galletas (20), y la parte del paquete de galletas (8). Dependiendo de lo que quieras estimar, puedes escribir tres fórmulas porcentuales distintas:

• La ecuación del porcentaje es esta: porcentaje = 100 × parte / total, y responde a la pregunta “qué porcentaje de 20 es 8”.
• la fórmula para la parte es parte = total × porcentaje / 100, y responde a “¿Cuál es el 40 % de 20?”.
• Y, por último, la fórmula para el total de galletas es: total = 100 × parte / porcentaje, y responde a “¿cuál es el 100 % si 8 es el 40 %?”.

Técnicamente, eso es todo. Ahora ya deberías saber cómo hallar el porcentaje de un número.

Aunque los antiguos romanos utilizaban los números romanos I, V, X, L, etc., los cálculos se realizaban a menudo en fracciones que se dividían por 100. Era equivalente al cálculo de porcentajes que conocemos hoy. Los cálculos con un denominador de 100 se hicieron más habituales tras la introducción del sistema decimal. Muchos textos medievales de aritmética aplicaban este método para describir las finanzas, por ejemplo, las tasas de interés. Sin embargo, el símbolo de porcentaje % que conocemos hoy solo se popularizó hasta hace poco, en el siglo XX, tras años de constante evolución.

El término porcentaje se atribuye a menudo al latín per centum, que significa por cien. Esto, en realidad, es incorrecto. El término procede del italiano per cento (por cien). El símbolo de porcentaje % evolucionó por la contracción gradual de esas palabras a lo largo de los siglos. Finalmente, cento adoptó la forma de dos círculos separados por una línea horizontal, de la que deriva el símbolo moderno %. La historia de los símbolos matemáticos es a veces asombrosa. ¡Te animamos a que investigues el origen del símbolo de la raíz cuadrada!

Últimamente, el símbolo de porcentaje se utiliza mucho en los lenguajes de programación como operador. Normalmente, representa la operación módulo. Por otra parte, en física experimental, el símbolo % tiene un significado especial. Se usa para expresar el error relativo entre el valor verdadero y el valor observado en una medición. Para saber más sobre el error relativo, puedes consultar nuestra calculadora de error porcentual 🇺🇸.

¿Te has encontrado alguna vez con un símbolo de porcentaje que tuviera un círculo adicional? ¡Eso no es un error! Hay dos símbolos relacionados:

• ‰, por mil y
• ‱, por diez mil, también conocido como punto base.

Más adelante explicaremos con más detalle qué significa “por mil”, qué es un punto base, y cómo convertir “por miles” y puntos base en porcentajes.

Las proporciones más grandes emplean otra notación (llamada “partes por notación”), por ejemplo, partes por millón (ppm), con la que frecuentemente se mide la concentración de una sustancia en solución o mezcla. La preocupación actual es el esmog, las diminutas partículas que entran en el aire y pueden afectar gravemente a la salud.

• “Por ciento” es una locución adverbial que se escribe en dos palabras y se emplea tras un elemento numérico para indicar una proporción en relación con cien unidades. Por ejemplo: “La pandemia aumenta un treinta por ciento los trastornos alimenticios”.
• “Porciento” es un sustantivo que significa “porcentaje”. Se usa principalmente en el área caribeña, aunque la forma mayoritaria en todo el ámbito hispánico es “porcentaje”. Por ejemplo: “El porciento de ocupación en espacios cerrados como restaurantes y centros comerciales se mantendrá operando sin cambios”.

Por mil, o simplemente ‰ es similar al porcentaje, solo que es una milésima (1/1000 o 0.001). Si el presupuesto de nuestro hogar es de 2400 $ y destinamos el 1 por mil de esa cantidad a comprar chicles, gastaríamos 2.4 $ (2 pesos con 40 centavos) en fastidiar a nuestros profesores mascando chicle (bueno, hace 20 años no estaba permitido en las escuelas polacas. Hoy en día no conocemos las normas 😃). Es bastante parecido a cómo se calculan los porcentajes. Si quisieras utilizar la calculadora de porcentajes para contar por mil, simplemente utiliza números 10 veces más bajos (0.2 en lugar de 2, o 4 en lugar de 40).

Por diez mil, punto base, o simplemente ‱, es una diezmilésima(1/10 000 o 0.0001). Es 10 veces más pequeño que por mil, así que para convertir puntos base en porcentajes, tienes que dividirlos por 100. ¡Así de sencillo!

Los puntos porcentuales 🇺🇸 son una bestia difícil de domar. Los utilizamos todo el tiempo, aunque no lo sepamos, y en estas situaciones, a menudo decimos incorrectamente porcentaje en lugar de punto porcentual. Una vez que leas esta sección, sabrás cómo hacerlo correctamente y te fastidiarás el resto de tu vida (porque otras personas seguirán cometiendo el error).

El senador Homero Simpson estaba en las encuestas con un 10 % el mes pasado. Desde entonces ha tenido unos cuantos debates con éxito, y ahora el 12 % de la población quiere votar por él. ¿Cuál es el cambio? Te tienta decir un 2 %, ¿verdad? ¡Está mal! Examinemos esto. Imagina que el total de la población es de 1000 personas. El 10 % de ellas son 100. El 12 % son 120. ¿Cuál es el incremento porcentual? ¡Es 100 × 20 / 100 = 20 %!

En esta situación es cuando resultan útiles los puntos porcentuales. Utilizamos los puntos porcentuales cuando queremos hablar de un cambio de un porcentaje a otro. Un cambio del 10 % al 12 % son dos puntos porcentuales (o 20 %).

La comprensión de los cambios en los porcentajes puede hacerse de dos maneras diferentes:

• Cambio en puntos porcentuales (pp): La diferencia entre dos valores porcentuales. Si un valor es el 10 % y el otro el 30 %, el cambio es de 20 puntos porcentuales (20 pp).
• Cambio en porcentaje: El cambio relativo entre dos valores porcentuales. Si un valor es el 10 % y el otro es el 30 %, el cambio es el 200 % del 10 % original.

Ahora, cuando lo sepas todo sobre los puntos porcentuales, te garantizamos que leerás u oirás a otras personas decir incorrectamente porcentaje cuando deberían utilizar puntos porcentuales. Si eres como nosotros, gritarás al periódico, insultándolo en un lenguaje inventado. Esto, además, ayudará a liberar espacio a tu alrededor cuando utilices el transporte público :-)