Calculatrice des pourcentages

Cette calculatrice des pourcentages est un outil qui vous permet de trouver la réponse à la question suivante : comment calculer un pourcentage par rapport à un chiffre ? Notre calculatrice est simple à utiliser. Il vous suffit de remplir deux champs, et le troisième sera calculé automatiquement pour vous. Vous vous demandez comment calculer un pourcentage en maths ou comment calculer le pourcentage d'un prix ? Lisez jusqu'à la fin !

Par ailleurs, notre calculatrice des pourcentages vous permet également d'effectuer des calculs dans le sens inverse, c'est-à-dire comment calculer le pourcentage d'un nombre. Jouez avec les champs pour voir la facilité d'utilisation de cet outil. Voulez-vous faire plus que juste trouver le pourcentage d'un nombre donné ?

En plus de faciliter l'apprentissage des pourcentages et des fractions 🇺🇸, cette calculatrice se révèle pratique dans de nombreuses situations. Les pourcentages font partie de notre vie quotidienne ! Quiconque s'est déjà rendu dans un centre commercial a certainement vu des douzaines de panneaux avec un signe pour cent accompagné du mot Soldes affichés en énorme. Et ce n'est qu'un exemple parmi tant d'autres de pourcentages. Ils apparaissent fréquemment, par exemple, dans le domaine de la finance, où nous les utilisons pour déterminer le montant de l'impôt sur le revenu ou de la TVA. Nous retrouvons aussi les pourcentages dans le domaine de la santé pour exprimer le taux de masse grasse ou de masse maigre.

Vous voyez, la formule de calcul du pourcentage est utile partout, non seulement au cours de maths.

Poursuivez votre lecture si vous souhaitez savoir comment calculer un pourcentage, quelle est la formule du pourcentage et quelles sont les applications des pourcentages dans d'autres domaines, comme les statistiques ou la physique.

Notre calculatrice des pourcentages comporte quatre sections. Les instructions suivantes devraient vous aider à sélectionner la bonne section et à l'utiliser à bon escient :

1. La section Quel est le p% de x ? calculera le pourcentage donné d'un nombre :

   1. Saisissez le pourcentage.
   2. Entrez le nombre dont vous devez trouver le pourcentage.
   3. Le nombre de pourcentages apparaît immédiatement.

Par exemple, supposons que vous ayez obtenu 80 % à un examen. Si l'épreuve était de 30 points, votre score est de 24 points.

Vous pouvez même faire le calcul inverse. Vous pouvez ainsi, par exemple, calculer votre pourcentage sur la base de votre note. Dans une épreuve de 30 points, si vous avez obtenu 27 points, votre pourcentage est de 90 %.

2. La section x est quel % de y ? déterminera le pourcentage de deux nombres donnés :

   1. Entrez le nombre dont vous voulez déterminer le pourcentage.

   2. Indiquez le nombre par rapport auquel ce pourcentage doit être évalué.

   3. Le calculateur vous donne instantanément le pourcentage.

Par exemple, supposons que le loyer de Gabin s'élève à 1 245 €  par mois, alors que son budget mensuel est de 4 000 €. En saisissant 1 245 dans le premier champ et 4 000 dans le second, nous pouvons déterminer que son loyer prend 31,125 % de son budget mensuel.

Cette section fonctionne également en sens inverse. Supposons que Gabin veuille bouger dans un endroit qui ne lui coûte pas plus de 25 % de son budget mensuel. Lorsque nous entrons 25 % comme pourcentage et 4 000 dans le deuxième champ, le calculateur nous informe que 1 000 € est le loyer maximum que Gabin peut se permettre.

3. La section x est p% de quoi ? est utile pour trouver la valeur pour laquelle un nombre donné comprend un pourcentage connu :

   1. Entrez le nombre pour lequel vous connaissez le pourcentage.

   2. Indiquez le pourcentage.

   3. Le calculateur vous donnera immédiatement le nombre que vous cherchez.

Voyons cela avec un exemple 10 est égal à 5 % de quel nombre ? Entrez 10 dans le premier champ et 5 % comme pourcentage. Vous voyez immédiatement que le résultat est 200.

Vous pouvez même utiliser cette méthode dans le sens inverse. En entrant 25 % et 50 dans le troisième champ, nous apprenons que 12,5 est 25 % de 50.

4. La section Quel est x augmenté/diminué de p% ? vous aidera à déterminer les effets d'une augmentation ou d'une diminution d'une valeur d'un pourcentage donné :

   1. Saisissez la valeur initiale.

   2. Sélectionnez si le changement est une augmentation ou une diminution.

   3. Saisissez le taux de variation de la valeur initiale.

   4. La valeur modifiée s'affiche instantanément.

Par exemple, supposons que le prix d'une barre chocolatée ait augmenté de 30 %. Saisissez le prix d'origine, soit 5 €, dans le premier champ. Ensuite, choisissez que le changement est une augmentation. Enfin, entrez 30 %, et vous apprendrez que le nouveau prix est de 6,50 €.

Cette méthode fonctionne également dans le sens inverse. Supposons que nous sachions que le prix réduit d'un article est de 44 €. Si la réduction est de 10 %, notre calculateur nous dira que le prix d'origine est de 48,89 €.

La section suivante contient de nombreuses informations fascinantes sur les pourcentages, en commençant par ce que sont les pourcentages et comment les trouver. Prenez donc de quoi grignoter et parcourez cette section.

Le pourcentage est l'une des nombreuses façons d'exprimer une relation sans dimension entre deux nombres (les autres méthodes étant les rapports et les fractions). Les pourcentages sont très populaires, car ils peuvent décrire des situations impliquant de grands nombres (par exemple, estimer les chances de gagner à la loterie), des moyennes (déterminer votre moyenne de français), ainsi que de très petits nombres (comme la proportion volumétrique de NO₂ dans l'air, fréquemment exprimée en PPM : parties par million).

Un pour cent est un centième. Le signe habituellement utilisé pour le pourcentage est %, mais il est parfois désigné par pct. Cela signifie que 5 pour cent est la même chose que 5 %, 5 pct, 0,05, 5/100, ou cinq centièmes. C'est aussi simple que cela, et cette calculatrice des pourcentages est un outil pour travailler avec des fractions décimales et des pourcentages. Si vous cherchez des problèmes plus compliqués, essayez de calculer le pourcentage d'un pourcentage 🇺🇸.

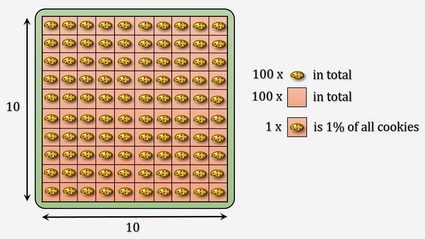
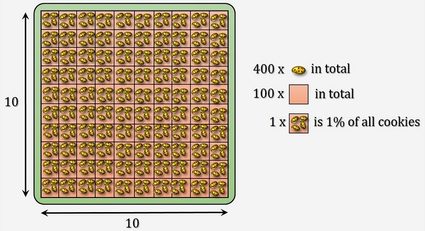
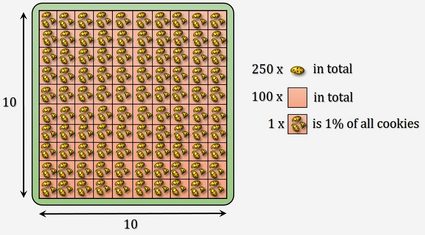
Tout cela est bien utile, mais nous n'utilisons généralement pas les pourcentages en tant que tels. Le plus souvent, nous voulons savoir l'importance d'un nombre par rapport à un autre nombre. Pour essayer de visualiser la notion de pourcentage, prenons un exemple gourmand. Supposons que vous ayez un grand paquet de cookies (ou de beignets ou de chocolats, comme vous préférez 😉). Essayons de trouver une réponse à la question suivante : que représente 40 % de 20 ? C'est 40 centièmes de 20, donc si nous divisions ces 20 cookies en 100 parts égales (bon courage !), 40 de ces parties représenteraient 40 % de 20 cookies. Faisons le calcul : 40/100 × 20 = 8. Un petit conseil pratique : pour diviser par 100, il suffit de déplacer la virgule de deux rangs vers la gauche. Dans notre calcul, 40/100 × 20 pourrait être remplacé par (40 × 20)/100 (c'est la même chose). 40 × 20 est égal à 800. En déplaçant la virgule de 800 de deux chiffres vers la gauche, vous obtenez 8,00, et lorsque vous vous débarrassez de tous les zéros inutiles, vous obtenez 8. Dans notre calculatrice, entrez 40 et 20 (ce qui donne 40 % de 20, soit 8).

Un pourcentage est également une façon d'exprimer la relation entre deux nombres sous la forme d'une fraction de 100. En d'autres termes, le pourcentage nous indique le rapport entre un nombre et un autre. Si nous savons que le nombre A représente 25 % du nombre B, nous savons que A par rapport à B est comme 25 par rapport à 100, ou, après une autre transformation, comme 1 par rapport à 4, c'est-à-dire que A est quatre fois plus petit que B. C'est ce que nous montre la calculatrice des pourcentages : qu'est-ce qu'un pourcentage et comment trouver le pourcentage de deux nombres.

Comment calculer le pourcentage de quelque chose ? Le plus simple est d'expliquer ce qu'est un pourcentage à l'aide de cookies. Il est surprenant de constater à quel point les cookies sauvent la mise, n'est-ce pas ? Supposons que nous ayons un grand tiroir avec 100 compartiments (une grille de 10 × 10). Chaque compartiment représente un centième ou 1 % de l'ensemble du tiroir. Nous remplissons ce tiroir de cookies de manière à obtenir exactement le même nombre de cookies dans chaque compartiment.

Commençons par l'exemple le plus simple avec 100 cookies. Comment obtenir le pourcentage de plusieurs cookies, disons, cinq ? La formule de calcul de ce pourcentage est très facile : chaque compartiment reçoit précisément un biscuit. Donc un pour cent de 100 est un biscuit, et cinq pour cent sont cinq cookies.

Choisissons un exemple un peu plus difficile et de quatre fois plus délicieux : 400 cookies ! Nous les répartissons de manière égale, et chaque compartiment reçoit quatre cookies. Les cookies paraissent plus petits, mais dans notre imagination, ils sont identiques, mais le tiroir est beaucoup plus grand ! Un pour cent de 400 est égal à 4. Que feraient 15 % ? C'est 15 compartiments multipliés par quatre cookies, soit 60 cookies. Nous commençons à avoir un peu mal au ventre, mais cela ne nous a jamais empêchés de manger plus de cookies !

Maintenant, quelque chose d'encore plus difficile : 250 cookies. Quelle sera la formule de calcul du pourcentage dans ce cas ? Nous avons divisé les 200 premiers cookies, en plaçant deux cookies dans chaque compartiment. Désormais, il nous reste 50 cookies qui doivent être ajoutés uniformément, humm, cela fait un demi-biscuit dans chaque compartiment. Comment calculer le pourcentage ? Vous avez raison : cette fois, 1 pour cent du nombre total de 250 cookies est 2,5. Combien y en a-t-il dans 15 compartiments ? 2,5 × 15 = 37,5.

N'oubliez pas que vous pouvez toujours vérifier ces résultats à l'aide de notre calculateur de pourcentage.

Et si vous en avez assez des cookies et que vous voulez découvrir comment calculer le pourcentage d'un prix, par exemple, vous ne devez pas aller trop loin ! Vous pouvez utiliser les instructions ci-dessus pour calculer n'importe quel pourcentage.

À quoi sert le pourcentage en maths ? Comme nous l'avons écrit précédemment, un pourcentage est une façon d'exprimer un rapport. Supposons que vous passiez un examen. Si nous vous disons que vous avez obtenu 123 points, cela ne vous dira rien.** En revanche, si nous vous disons que vous avez obtenu 82 %, ce chiffre est une information plus compréhensible. Même si nous vous disons que vous avez obtenu 123 points sur 150, il est plus difficile de savoir à quel point vous avez réussi. Une semaine plus tôt, il y a eu un autre examen, et vous avez obtenu 195 sur 250, soit 78 %. S'il est difficile de comparer 128 sur 150 à 195 sur 250, il est facile de dire qu'une note de 82 % est meilleure que 78 %. Le pourcentage n'est-il pas utile ?

Qu'en est-il des fractions décimales et des pourcentages ? Les pourcentages peuvent facilement être convertis en décimales. Il suffit de diviser le pourcentage par 100, et le tour est joué. 15 % équivaut à 0,15. Comme nous l'avons montré précédemment, 0,15 de 250 cookies correspond à 37,5 %.

En chimie ou en physique, les pourcentages sont parfois mieux adaptés à l'expression de diverses quantités que les fractions décimales. Par exemple, il est beaucoup plus commode de dire que la concentration en pourcentage d'une substance spécifique est de 15,7 % que de dire qu'il y a 18,66 g de substance dans 118,66 g de solution. Un autre exemple est celui du rendement (ou de son cas particulier, le cycle de Carnot). Est-il préférable de dire qu'un moteur de voiture fonctionne avec un rendement de 20 % ou qu'il produit une énergie de 0,2  kWh à partir d'une énergie de 1 kWh ? Qu'en pensez-vous ? Nous sommes convaincus que vous êtes déjà conscient de l'importance de savoir calculer un pourcentage à partir d'un nombre. C'est une compétence vraiment utile !

Il est certes rapide et facile d'utiliser notre calculatrice des pourcentages, mais vous n'avez pas toujours accès à un ordinateur ou à un smartphone. De plus, il est tout simplement génial de pouvoir effectuer des calculs dans votre tête. Peut-être pas autant que de jongler avec des torches enflammées, mais presque.

Le pourcentage vous indique le rapport entre un nombre A et un nombre B. Voici un exemple concret : il y a deux filles dans un groupe de cinq enfants. Quel est le pourcentage de filles ? En d'autres termes, nous voulons savoir quel est le rapport entre les filles et l'ensemble des enfants. C'est 2 sur 5, ou 2/5. Nous appelons le premier nombre (2) numérateur et le deuxième nombre (5) dénominateur, car il s'agit d'une fraction. Pour calculer le pourcentage, multipliez cette fraction par 100 et ajoutez le signe de pourcentage. 100 × numérateur / dénominateur = pourcentage. Dans notre exemple, c'est 100 × 2/5 = 100 × 0,4 = 40. Quarante pour cent des membres du groupe sont des filles. Voilà comment faire pour convertir les fractions décimales en pourcentages.

La simplification des fractions est difficile pour vous ? La meilleure façon de résoudre ce problème est de trouver le PGCD (plus grand commun diviseur) du numérateur et du dénominateur et de les diviser tous les deux par le PGCD.

Procédons à l'inverse et essayons de trouver le numérateur. C'est une autre fonction de notre calculateur de pourcentage. Disons que vous savez que 70 % des fruits dans le panier sont des pommes et qu'il y a 30 fruits en tout. La situation pourrait être pire : il pourrait s'agir de citrons. Combien de pommes avons-nous donc ? Obtenons notre formule de pourcentage : 100 × numérateur / dénominateur = pourcentage. Nous voulons trouver le numérateur. Divisez les deux côtés par 100 (pour vous débarrasser du 100 à gauche), puis multipliez les deux côtés par le dénominateur. Voici ce que nous obtenons : numérateur = pourcentage × dénominateur / 100. Remplaçons le pourcentage et le dénominateur par nos valeurs : numérateur = 70 × 30 / 100. Maintenant, c'est facile : numérateur = 2 100 / 100 = 21, nous avons 21 pommes. Cela devrait suffire pour le déjeuner ou pour une bagarre assez violente.

Cette procédure peut être appliquée dans n'importe quel contexte. Vous voulez savoir comment calculer le pourcentage d'un prix ? Procédez de la même manière, et vous arriverez à votre résultat.

Résolvons à présent un problème avec un dénominateur inconnu. Nous avons dépensé 30 % de notre argent de poche pour acheter des chewing-gums (nous n'avons jamais dit que nous étions de grands investisseurs). Nous avons acheté 12 paquets pour 1 € chacun. Vous savez donc que 12 € représentaient 30 % de notre budget total. De combien d'argent disposions-nous avant de tout gaspiller ? Commençons par notre formule : 100 × numérateur / dénominateur = pourcentage ou 100 × 12 / dénominateur = 30. Cette fois-ci, nous voulons trouver le dénominateur. Multiplions les deux côtés par le dénominateur, puis divisons par le pourcentage. Nous obtiendrons ainsi 100 × 12 / 30 = dénominateur. Et inversement, dénominateur = 100 × 12 / 30 = 1 200 / 30 = 40. Nous avions 40 € et nous en avons dépensé 30 %, soit 12 € en chewing-gum. Cela en valait vraiment la peine.

Pour reprendre nos exemples de cookies, nommons les trois parties de notre équation : le pourcentage de cookies, 40 %, le paquet entier de cookies, 20, et la partie du paquet de cookies, 8. En fonction de ce que vous voulez estimer, vous pouvez écrire trois formules de pourcentage différentes.

• La formule de calcul du pourcentage d'un entier est la suivante : pourcentage = 100 × partie / tout, et elle répond à la question : « Quel pourcentage de 20 est égal à 8 ? ».
• La formule pour une partie est la suivante : partie = entier × pourcentage / 100, et elle répond à la question « Que représente 40 % de 20 ? ».
• Enfin, la formule pour l'entièreté est : entier = 100 × partie / pourcentage, et elle répond à la question « Quel est le pourcentage de 100 % si 8 représente 40 % ? ».
• Pour rendre le tout plus facile, n'hésitez pas à utiliser notre calculatrice des pourcentages ! Vous ne devrez recourir à aucune formule.

C'est techniquement tout. Vous savez maintenant comment trouver le pourcentage d'un nombre.

Bien que les anciens Romains aient utilisé les chiffres romains I, V, X, L, et ainsi de suite, les calculs étaient souvent effectués sous forme de fractions divisées par 100. C'était l'équivalent du calcul des pourcentages que vous connaissez aujourd'hui. Les calculs avec un dénominateur de 100 sont devenus plus courants après l'introduction du système décimal. De nombreux textes arithmétiques médiévaux ont appliqué cette méthode pour gérer les finances, par exemple les taux d'intérêts. Cependant, le signe de pourcentage % que nous connaissons aujourd'hui n'est devenu populaire qu'assez récemment, au XXᵉ siècle, après des années d'évolution constante.

Le terme pourcentage est généralement attribué au latin per centum, qui signifie par cent. En fait, c'est faux. Le terme vient de l'italien per cento : pour cent. Le signe pour cent (%) est né de la contraction progressive de ces mots au cours des siècles. Finalement, cento a pris la forme de deux cercles séparés par une droite horizontale, d'où le symbole % moderne est dérivé. L'histoire des symboles mathématiques est parfois étonnante. Nous vous encourageons à jeter un coup d'œil sur l'origine du symbole de la racine carrée !

De plus, le symbole du pourcentage est largement utilisé dans les langages de programmation en tant qu'opérateur. En général, il représente l'opération modulo. À maints égards, en physique expérimentale, le symbole % a une signification particulière. Il est utilisé pour exprimer l'erreur relative entre la valeur réelle et la valeur observée lors d'une mesure. Pour en savoir plus sur l'erreur relative, vous pouvez consulter notre calculateur de pourcentage d'erreur 🇺🇸.

Avez-vous déjà rencontré un symbole de pourcentage comportant un cercle supplémentaire ? Ce n'est pas une erreur ! Il existe différents signes :

• ‰ – pour mille
• ‱ – pour dix mille (aussi connu, sous le terme : point de base)

Plus loin dans le texte, nous expliquons plus en détail ce que signifie le pour mille, ce qu'est un point de base et comment convertir les pour mille et les points de base en pourcentages.

Les proportions plus élevées utilisent d'autres notations (appelées notations par partie), par exemple les parties par million (PPM) qui sont fréquemment utilisées pour mesurer la concentration d'une substance dans une solution ou un mélange. Le smog, ces minuscules particules qui pénètrent dans l'air et peuvent nuire gravement à la santé, est un sujet de préoccupation actuel.

Le pour mille, ou ‰ est similaire au pourcentage, sauf qu'il s'agit d'un millième (1/1000 ou 0,001). Si le budget de notre ménage est de 2 400 € et que nous en consacrons 1 pour mille à l'achat de chewing-gum, nous dépenserons 2,4 € (2 € 40) pour avoir une haleine mentholée. C'est assez semblable à la façon dont vous trouvez les pourcentages. Si vous vouliez utiliser une calculatrice des pourcentages pour compter pour mille, il vous suffirait d'utiliser des nombres 10 × plus petits (0,2 au lieu de 2 ou 4 au lieu de 40).

Pour dix mille, point de base ou simplement ‱ est un dix-millième (1/10 000 ou 0,000 1). C'est 10 × plus petit que le pour mille, donc pour convertir les points de base en pourcentages, vous devez les diviser pour 100. C'est aussi simple que cela !

Les points de pourcentage sont un peu délicats, comme des créatures fragiles. Nous les utilisons fréquemment, même sans nous en rendre compte, et dans ces cas, nous avons souvent tendance à confondre à tort « pourcentage » avec « point de pourcentage ».

Notre calculateur de pourcentage ne calcule pas les points de pourcentage, mais nous vous invitons à consulter le calculateur de points de pourcentage 🇺🇸 si vous êtes curieux ou curieuse !

Une fois que vous aurez lu cette section, vous saurez comment le calculer correctement et vous serez ennuyé pour le reste de votre vie (parce que d'autres personnes continueront à faire l'erreur).

Le mois dernier, le député Titeuf était crédité de 10 % dans les sondages. Depuis, il a participé à quelques débats réussis et, aujourd'hui, 12 % de la population souhaite voter pour lui. Quel est le changement en pourcentage ? Vous voulez dire 2 %, n'est-ce pas ? Eh bien, c'est faux ! Examinons la situation. Imaginez que la population totale soit de 1 000 personnes. 10 % représente 100. 12 %, c'est 120. Quel est le pourcentage d'augmentation ? C'est 100 × 20 / 100 = 20 % !

C'est dans cette situation que les points de pourcentage s'avèrent utiles. Nous utilisons les points de pourcentage lorsque nous voulons parler d'un changement d'un pourcentage à un autre. Une variation de 10 à 12 % représente deux points de pourcentage (ou 20 %).

Il existe deux façons de comprendre les variations en pourcentages.

• Variations en points de pourcentage (pp) : La différence entre deux valeurs de pourcentage. Si une valeur est de 10  % et l'autre de 30 %, la variation est de 20 points de pourcentage (20 pp).
• Variation en pourcentage : la variation relative entre deux valeurs en pourcentage. Si l'une des valeurs est de 10 % et l'autre de 30 %, la variation est de 200 % des 10 % initiaux.

Maintenant que vous savez tout sur les points de pourcentage, nous vous garantissons que vous lirez ou entendrez d'autres personnes dire à tort pourcentage alors qu'elles devraient utiliser les points de pourcentage. Si vous êtes comme nous, vous hurlerez dans votre barbe.

Mateusz et Dominik ont l'habitude de créer des outils scientifiques qui permettent de résoudre des problèmes quotidiens et d'expliquer les concepts de manière simple et facile à assimiler. L'idée de ce calculateur de pourcentage est née lorsque Mateusz faisait des achats en ligne et comparait les prix et les pourcentages de réduction sur différents sites web. Aujourd'hui, il l'utilise non seulement pour prendre de meilleures décisions d'achat, mais aussi pour choisir de meilleurs investissements.

Nous apportons un soin particulier à la qualité du contenu afin de garantir qu'il soit aussi précis et fiable que possible. Chaque outil est évalué par un expert qualifié, puis relu par un locuteur natif. Si vous souhaitez en savoir plus sur nos normes, veuillez consulter notre politique éditoriale.