Calculateur d'accélération

Notre calculateur d'accélération est un outil qui vous aide à déterminer la rapidité avec laquelle la vitesse d'un objet change. Il fonctionne de trois manières différentes, basées sur :

1. La différence entre les vitesses à deux moments distincts.
2. La distance parcourue pendant l'accélération.
3. La masse d'un objet en accélération et la force qui agit sur lui.

Si vous vous demandez ce qu'est l'accélération, sa formule, ou les unités d'accélération, continuez à lire pour en apprendre plus sur l'accélération. Cette dernière est strictement liée au mouvement d'un objet, et tout objet en mouvement possède une énergie spécifique.

Pour que les choses soient claires, nous avons également préparé quelques exemples d'accélération qui sont fréquents en physique. Vous les trouverez ici :

1. Accélération centripète et accélération tangentielle.
2. Accélération angulaire.
3. Accélération gravitationnelle.
4. Accélérateur de particules.

L'accélération se produit toujours lorsqu'une force non nulle agit sur un objet. Vous pouvez la ressentir dans un ascenseur lorsque vous devenez un peu plus lourd (accélération) ou plus léger (décélération) ou lorsque vous descendez une pente raide avec une luge. De plus, comme vous le savez, grâce à la théorie générale de la relativité, l'Univers tout entier est non seulement en expansion, mais il s'agit même d'une expansion accélérée ! Cela signifie que la distance entre deux points est de plus en plus grande, mais nous ne le ressentons pas au quotidien, car toutes les échelles du monde s'étendent également.

L'accélération est le taux de variation de la vitesse d'un objet. En d'autres termes, c'est la rapidité à laquelle la vitesse change. Selon la deuxième loi de Newton 🇺🇸, l'accélération est directement proportionnelle à la somme de toutes les forces qui agissent sur un objet et inversement proportionnelle à sa masse. C'est une question de bon sens : si plusieurs forces différentes poussent un objet, vous devez calculer leur somme (elles peuvent travailler dans des directions différentes), puis diviser la force résultante par la masse de l'objet.

Cette définition de l'accélération indique que l'accélération et la force sont, en fait, la même chose. Lorsque la force change, l'accélération change également, mais l'intensité de ce changement dépend de la masse de l'objet (voir notre calculateur d'amplitude d'accélération 🇺🇸 pour plus de détails). Cela n'est pas vrai dans une situation où la masse change également, par exemple dans la poussée d'une fusée, lorsque des propergols brûlés sortent de la tuyère de la fusée. Consultez notre calculateur de poussée de fusée 🇺🇸 pour en savoir plus.

On peut mesurer l'accélération subie par un objet directement à l'aide d'un accéléromètre. Si vous accrochez un objet à l'accéléromètre, il affichera une valeur non nulle. Comment cela se fait-il ? Eh bien, c'est à cause des forces gravitationnelles qui agissent sur toutes les particules qui ont une masse. Et là où il y a une force, il y a une accélération. Un accéléromètre au repos mesure donc l'accélération de la gravité, qui, à la surface de la Terre, est d'environ 9,806 65 m⋅s⁻². En d'autres termes, il s'agit de l'accélération due à la gravité que subit tout objet en chute libre lorsqu'il est dans le vide.

En parlant de vide, avez-vous déjà regardé Star Wars ou un autre film qui se déroule dans l'espace ? Les batailles épiques de vaisseaux spatiaux, le bruit des blasters, des moteurs et des explosions. Eh bien, c'est un mensonge. L'espace est un vide, et aucun son ne peut y être entendu (les ondes sonores exigent de la matière pour se propager). Ces batailles devraient être silencieuses ! Dans l'espace, personne ne peut vous entendre crier.

Le calculateur d'accélération d'Omni ne prend en compte que la situation dans laquelle un objet a une accélération uniforme (constante). Dans ce cas, l'équation de l'accélération est, par définition, le rapport de la variation de la vitesse sur un temps donné.

Vous pouvez aussi apprendre à trouver l'accélération de deux autres manières. Voyons comment utiliser notre calculateur (vous trouverez les équations d'accélération dans la section suivante).

• Selon les données dont vous disposez, vous pouvez calculer l'accélération de trois manières différentes. Tout d'abord, sélectionnez une option appropriée (« Différence entre les vitesses », « Distance parcourue » ou « Masse et force »).

• Pour la différence entre les vitesses : saisissez les vitesses initiale v_i et finale v_f de l'objet et le temps Δt qu'il a fallu pour que la vitesse change (voir notre calculateur de vitesse si cela est nécessaire).

• Pour la distance parcourue : entrez la vitesse initiale v_i, la distance parcourue Δd et le temps Δt passé pendant l'accélération. Ici, vous n'avez pas besoin de connaître la vitesse finale.

• Pour la masse et la force : entrez la masse m de l'objet et la force F agissant sur cet objet. Il s'agit d'un ensemble de variables entièrement différent qui découle de la deuxième loi de Newton (autre définition de l'accélération).

• Lisez l'accélération résultante dans le dernier champ. Vous pouvez également effectuer des calculs dans l'autre sens si vous savez ce qu'est l'accélération, par exemple pour estimer la distance Δd. Il vous suffit de fournir le reste des paramètres dans ce champ.

Au XVII^e siècle, Sir Isaac Newton, l'un des scientifiques les plus influents de tous les temps, a publié son célèbre ouvrage Principia. Il y formule la loi de la gravitation universelle, qui stipule que deux objets de masse s'attirent avec une force qui dépend exponentiellement de la distance qui les sépare (elle est inversement proportionnelle au carré de la distance). Plus les objets sont lourds, plus la force gravitationnelle est importante. Cela explique, par exemple, pourquoi les planètes gravitent autour du Soleil, car ce dernier est très dense.

Dans Principia, Newton inclut également trois lois qui sont essentielles pour comprendre la physique de notre monde. Le calculateur d'accélération est basé sur trois équations d'accélération différentes, la troisième étant dérivée des travaux de Newton :

1. a = (v_f - v_i) / Δt
2. a = 2 × (Δd - v_i × Δt) / Δt²
3. a = F / m

où :

• a – accélération
• v_i et v_f – respectivement les vitesses initiale et finale
• Δt – temps d'accélération
• Δd – distance parcourue pendant l'accélération
• F – force agissant sur un objet qui accélère
• m – masse de l'objet

Vous savez maintenant comment calculer l'accélération ! Dans le prochain paragraphe, nous aborderons les unités d'accélération (SI et impériales).

Si vous savez déjà comment calculer l'accélération, concentrons-nous sur les unités d'accélération. Vous pouvez les déduire des équations que nous avons énumérées ci-dessus. Tout ce que vous devez savoir, c'est que la vitesse est exprimée en pieds par seconde (système impérial/US) ou en mètres par seconde (système SI) et le temps en secondes. Par conséquent, si vous divisez la vitesse par le temps (comme nous le faisons dans la première formule d'accélération), vous obtiendrez l'unité d'accélération ft⋅s⁻² ou m⋅s⁻² selon le système que vous utilisez.

Vous pouvez également utiliser la troisième équation. Dans ce cas, vous devez diviser la force (poundals aux États-Unis et newtons pour SI) par la masse (livres aux États-Unis et kilogrammes pour SI), ce qui donne pdl⋅lb⁻¹ ou N⋅kg⁻¹. Les deux représentent la même chose, puisque le poundal est pdl = lb⋅ft⋅s⁻² et le newton est N = kg⋅m⋅s⁻². En les remplaçant et en réduisant les unités, vous obtiendrez (lb⋅ft⋅s⁻²) / lb = ft⋅s⁻² ou (kg⋅m⋅s²) / kg = m⋅s⁻².

Il existe par ailleurs une troisième option qui est, en fait, largement utilisée. Vous pouvez exprimer l'accélération par l'accélération normale de la pesanteur terrestre, qui est définie comme g = 9,806 65 m⋅s⁻². Par exemple, si vous dites qu'un ascenseur se déplace vers le haut avec une accélération de 0,2 g, cela signifie qu'il accélère d'environ 6,2 ft⋅s⁻² ou 2 m⋅s⁻² (c'est-à-dire 0,2 × g). Nous avons arrondi les expressions ci-dessus à deux chiffres significatifs.

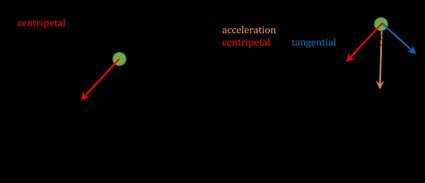
Accélération centripète et accélération tangentielle

L'accélération est généralement un vecteur, vous pouvez donc toujours la décomposer en composantes. En général, nous avons deux parties perpendiculaires l'une à l'autre : l'accélération centripète et l'accélération tangentielle. L'accélération centripète change la direction de la vitesse, et donc la forme de la trajectoire, mais n'affecte pas la valeur de la vitesse. En revanche, l'accélération tangentielle est toujours parallèle à la trajectoire du mouvement. Elle modifie uniquement la valeur de la vitesse, et non sa direction.

Dans un mouvement circulaire (l'image la plus à gauche ci-dessous), où un objet se déplace autour de la circonférence d'un cercle, il n'y a que la composante centripète. Un objet gardera sa vitesse à une valeur constante. Pensez à la Terre, qui a une accélération centripète due à la gravité du Soleil (en fait, sa vitesse change un peu au cours d'une année).

Lorsque les deux composantes sont présentes, la trajectoire de l'objet ressemble à l'image ci-contre. Que se passe-t-il s'il n'y a qu'une accélération tangentielle ? Il s'agit alors d'un mouvement linéaire. C'est comme lorsque vous appuyez sur l'accélérateur d'une voiture sur une partie droite de l'autoroute.

Accélération angulaire

L'accélération angulaire joue un rôle essentiel dans la description du mouvement de rotation. Cependant, ne la confondez pas avec les accélérations centripète et tangentielle mentionnées précédemment. Cette quantité physique correspond au taux de variation de la vitesse angulaire. En d'autres termes, elle vous indique à quelle vitesse les rotations d'un objet s'accélèrent : l'objet tourne de plus en plus vite (ou de plus en plus lentement si l'accélération angulaire est inférieure à zéro). Consultez notre calculateur d'accélération angulaire 🇺🇸 pour plus d'informations.

Savez-vous qu'il existe une analogie entre cette loi et la loi de Newton sur la dynamique du mouvement de rotation ? Dans sa deuxième loi, si vous remplacez l'accélération par l'accélération angulaire, la force par le couple et la masse par le moment d'inertie, vous obtiendrez l'équation de l'accélération angulaire. Vous remarquerez peut-être que certaines lois physiques, comme celle-ci, sont universelles, ce qui les rend très importantes en physique.

Accélération gravitationnelle

Nous avons déjà mentionné l'accélération gravitationnelle à plusieurs reprises. Elle résulte de la force gravitationnelle qui existe entre deux objets ayant une masse (notez que l'équation de la gravité ne dépend pas du volume d'un objet : seule la masse est essentielle ici). Cela peut sembler étrange à première vue, mais selon la troisième loi de Newton, vous agissez sur la Terre avec la même force que la Terre agit sur vous. Cependant, la masse de la Terre est beaucoup plus importante que la masse d'un être humain (~10²² fois plus importante), ainsi notre impact sur la Terre est pratiquement nul. C'est un peu comme toutes les bactéries (~10¹⁸ fois plus légères qu'un être humain) qui vivent sur votre main. Vous ne les remarquez même pas ! D'un autre côté, nous pouvons ressentir l'influence de notre planète, à savoir l'accélération gravitationnelle.

La gravité standard est, par définition, de 9,806 65 m⋅s⁻². Par conséquent, si un humain pèse environ 100 kg, il est soumis à une force gravitationnelle d'environ 1 000 N. Entrons cette valeur dans le troisième champ de notre calculateur ainsi que la masse de la Terre 5,972 × 10²⁴ kg en notation scientifique. Quelle est l'accélération calculée ? Elle est si faible que notre calculateur la considère comme nulle. Nous ne sommes rien par rapport à la planète !

Accélérateur de particules

Après avoir parlé des énormes objets de l'espace, allons vers le monde microscopique des particules. Bien que nous ne puissions pas les voir de nos yeux, nous avons réussi à maîtriser des particules de haute énergie, comme les électrons et les protons. Nous les utilisons régulièrement dans les accélérateurs de particules, couramment utilisé en physique, en chimie et en médecine. Nous les utilisons pour tuer les cellules cancéreuses tout en épargnant les tissus sains environnants ou pour étudier la structure d'un matériau à l'échelle atomique.

Vous savez sans doute que le Grand collisionneur de hadrons (CERN) est l'accélérateur de particules le plus puissant au monde. Il nous permet d'aller plus loin pour comprendre comment l'univers travaille et de développer des technologies qui pourraient avoir de nombreuses applications essentielles à l'avenir. Cependant, pour atteindre des énergies aussi élevées, nous devons accélérer les particules à des vitesses proches de celle de la lumière. En bref, nous pouvons le faire en utilisant des champs magnétiques ou électriques.