Polar Form Calculator

Q: What are the forms of a complex number?

The two main forms of a complex number are polar and rectangular . Usually, you first encounter the rectangular form z = a + bi , where a and b are the real part and imaginary part of z , respectively. They are both real numbers! The polar form describes z by r × exp(φi) , where: The magnitude r is the distance from the origin (0,0) to z ; and The argument φ is the angle between the real axis (x-axis) and the radius connecting the origin (0,0) and z .

Q: How do I convert from rectangular to polar form?

To convert a complex number from the rectangular a + bi to polar form z , we use the formulas: r = √(a² + b²) and φ = atan2(b, a) .

Q: How do I convert from trigonometric to polar form?

To convert a complex number from trigonometric to polar form, you need to: Make sure your number is written as z = r × cos(φ) + r × i × sin(φ)] . Extract the magnitude r and the argument φ . Write down your number as r × exp(φi) . If in doubt, use an online polar form calculator.

Q: What is the polar form of -1?

The answer is exp(πi) . To derive this answer, observe that the modulus (magnitude) of -1 is equal to 1 . Next, we must determine φ such that cos(φ) = -1 and sin(φ) = 0 . We easily verify that φ = π satisfies these conditions. Hence, the whole number reads 1 × exp(πi) , as claimed.

Creators

Anna Szczepanek, PhD

Anna SzczepanekPhD, Jagiellonian University in Kraków, Poland

Website

Anna Szczepanek, PhD is a mathematician at the Faculty of Mathematics and Computer Science of the Jagiellonian University in Kraków, where she researches mathematical physics and applied mathematics. At Omni, Anna uses her knowledge and programming skills to create math and statistics calculators. In her free time, she enjoys hiking and reading. See full profile

Check our editorial policy

Reviewers

Komal Rafay

Komal has a master's in Bioinformatics, with 3+ years of experience as a project manager. She has a vast experience of 7+ years in teaching Math, Computer science, and General Sciences, not only professionally but also helping out local children. Komal is an enthusiastic reader with a thirst for knowledge. As a side hustle that satisfies her love for art, she is a body art and henna expert. In her free time, you will find her reading books, writing short stories, playing with her pets, or experimenting with food while listening to some bouncy music. See full profile

Check our editorial policy

Omni's polar form calculator can help whenever you want to convert a complex number from rectangular to polar form. Scroll down to find a short article explaining what the different forms of a complex number are all about and what the polar form conversion formulas look like. Believe it or not, converting to polar form can be fun!

What are the forms of a complex number?

The two main forms of a complex number are polar and rectangular. Usually, you first encounter the rectangular form z = a + bi, where a and b are the real part and imaginary part of z, respectively. They are both real numbers!

The polar form describes z by r × exp(φi), where:

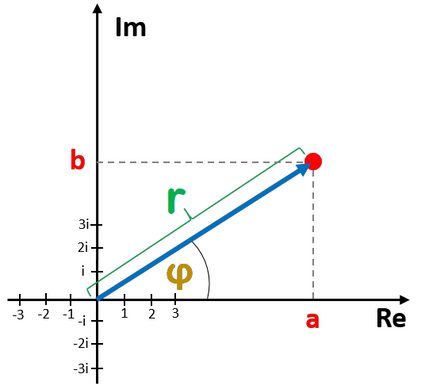
The magnitude r is the distance from the origin (0,0) to z; and
The argument φ is the angle between the real axis (x-axis) and the radius connecting the origin (0,0) and z.

Look at the picture to better understand what the polar form is:

How do I convert from rectangular to polar form?

To convert a complex number from the rectangular a + bi to polar form z, we use the formulas:

r = √(a² + b²)

and

φ = atan2(b, a).

If a > 0, then atan2(b, a) = arctan(b / a). However, if a < 0, then atan(b /a) does not give us the correct angle - it must be corrected by ±π to send us into the correct quadrant of the plane. Formally atan2(b, a) is defined as:

atan(b / a) if a > 0;
atan(b / a) + π if a < 0 ≤ b;
atan(b / a) - π if a,b < 0;
π/2 if a = 0 < b;
-π/2 if b < 0 = a; and
remains undefined if x = y = 0.

These are exactly the formulas behind Omni's polar form converter.

How to use this polar form calculator?

To use this polar form converter, take a complex number in the rectangular form a + bi and input a and b into the respective fields of our tool. The two ingredients of the polar form will appear immediately in their fields: the magnitude r and phase (argument) φ. Take them and write down the polar form r × exp(iφ) of your number.

This can't get any easier!

Omni tools for complex numbers

Complex numbers can find you in sooo many areas of science! Omni is well aware of that - we have built a whole collection of tools addressing different problems related to complex numbers. Make sure to check out at least a few of the following tools:

FAQs

How do I convert from trigonometric to polar form?

To convert a complex number from trigonometric to polar form, you need to:

Make sure your number is written as z = r × cos(φ) + r × i × sin(φ)].
Extract the magnitude r and the argument φ.
Write down your number as r × exp(φi).
If in doubt, use an online polar form calculator.

What is the polar form of -1?

The answer is exp(πi). To derive this answer, observe that the modulus (magnitude) of -1 is equal to 1. Next, we must determine φ such that cos(φ) = -1 and sin(φ) = 0. We easily verify that φ = π satisfies these conditions. Hence, the whole number reads 1 × exp(πi), as claimed.