Square Root Calculator

Our square root calculator estimates the square root of any positive number you want. Just enter the chosen number and read the results. Everything is calculated quickly and automatically! With this tool, you can also estimate the square of the desired number (just enter the value into the second field) and use it to find perfect squares from the square root formula.

Are you struggling with adding, subtracting, multiplying, dividing, or simplifying square roots? Not anymore! The following text will teach you how to perform these operations.

Have you ever wondered about the origin of the square root symbol √? We can assure you that its history is not as simple as you might think at first. The origin of the root symbol goes back to ancient times, as does the origin of the percent — keep reading to learn more!

If you're looking for the square root graph or square root function properties, head directly to the appropriate section (just click the links above!). There, we explain how to compute the derivative of a square root; we also elaborate on how to calculate the square roots of exponents or fractions. Finally, if you are persistent enough, you will find out that it is, in fact, possible to obtain the square root of a negative number. To do this, we need complex numbers which have broad applications in physics and mathematics.

Square roots were already known in antiquity. The earliest clay tablet with the correct value of √2 = 1.41421 up to 5 decimal places comes from Babylonia (1800 BCE - 1600 BCE). Many other documents show that square roots were also used by the ancient Egyptians, Indians, Greeks, and Chinese. However, the origin of the root symbol √ is still largely speculative.

• Many scholars believe that square roots originate from the letter "r" — the first letter of the Latin word radix meaning root.
• According to another theory, the square root symbol was taken from the Arabic letter ج that was placed in its original form of ﺟ in the word جذر — root (the Arabic language is written from right to left).

The first use of the square root symbol √ didn't include the horizontal "bar" over the numbers inside the square root (or radical) symbol, √‾. The "bar" is known as vinculum in Latin, meaning bond. Although the radical symbol with vinculum is now in everyday use, it is often omitted, e.g., in online texts. The notation of higher-degree roots was introduced by Albert Girard, who placed the degree index within the opening of the radical sign, e.g., ³√ or ⁴√.

We have explained how the root symbol √ came into being, but why are roots called this way in the first place? The choice of the name "root" becomes more evident if we recast the equation x = ⁿ√a as xⁿ = a. The number x is called a root or radical because it is the hidden base of a. Thus, the word radical doesn't mean far-reaching or extreme, but instead foundational, reaching the root cause.

What about the "square" part in the name of "square roots"? Geometrically, the square root √x is the side length of a square of area x — hence the name. Likewise, the third root ∛ is often called "cube root" because ∛x is the edge length of a cube of volume x. Thus, square roots are ubiquitous in planar geometry, while cube roots appear frequently in 3-dimensional geometry. The emergence of roots in simple geometric problems explains why radicals had already been of interest to humanity several thousand years ago.

In mathematics, the traditional operations on numbers are addition, subtraction, multiplication, and division. Nonetheless, we sometimes add more advanced operations to this list: taking square roots, exponentiation, and taking logarithms. In this article, we will focus on taking square roots.

The square root definition of a given number x is every number y whose square y² = y × y yields the original number x. Note that y² = (-y) × (-y) as well. Therefore, the square root formula can be expressed as:

y = ±√x ⟺ y² = x

where ⟺ is a mathematical symbol that means if and only if. Each positive real number always has two distinct square roots — the first is positive, and the second is negative. By contrast, 0 has only one root — itself. Remember that with the symbol √x, we always denote the non-negative root of x!

There is another common way to denote square roots, which expresses the square root in terms of a fractional power:

√x = x^1/2 = x^0.5

The rationale for this notation is that:

(x^0.5)² = x^{0.5 × 2} = x

Maybe we aren't being very modest, but we think that the best answer to the question of how to find the square root is straightforward: use the square root calculator! You can use it both on your computer and your smartphone to quickly estimate the square root of a given number. Unfortunately, there are sometimes situations when you can only rely on yourself. What then? To prepare for this, you should remember several basic perfect square roots:

• Square root of 1: √1 = 1, since 1 × 1 = 1;

• Square root of 4: √4 = 2, since 2 × 2 = 4;

• Square root of 9: √9 = 3, since 3 × 3 = 9;

• Square root of 16: √16 = 4, since 4 × 4 = 16;

• Square root of 25: √25 = 5, since 5 × 5 = 25;

• Square root of 36: √36 = 6, since 6 × 6 = 36;

• Square root of 49: √49 = 7, since 7 × 7 = 49;

• Square root of 64: √64 = 8, since 8 × 8 = 64;

• Square root of 81: √81 = 9, since 9 × 9 = 81;

• Square root of 100: √100 = 10, since 10 × 10 = 100;

• Square root of 121: √121 = 11, since 11 × 11 = 121; and

• Square root of 144: √144 = 12, since 12 × 12 = 144.

The above numbers are the simplest square roots because every time you obtain an integer. Try to remember them! But what can you do when a number doesn't have such a nice square root? There are multiple solutions. First of all, you can try to predict the result by trial and error. Let's say that you want to estimate the square root of 52:

1. You know that √49 = 7 and √64 = 8, so √52 should be between 7 and 8.

2. Number 52 is closer to the 49 (effectively closer to the 7), so you can try guessing that √52 is 7.3.

3. Then, you square 7.3, obtaining 7.3² = 53.29 (as the square root formula says), which is higher than 52. You have to try with a smaller number, let's say 7.2.

4. The square of 7.2 is 51.84. Now you have a smaller number, but much closer to the 52. If that accuracy satisfies you, you can end estimations here. Otherwise, you can repeat the procedure with a number chosen between 7.2 and 7.3,e.g., 7.22, and so on and so forth.

Another approach is to simplify the square root first and then use approximations for square roots of the prime numbers (typically rounded to two decimal places):

• Square root of 2: √2 ≈ 1.41;
• Square root of 3: √3 ≈ 1.73;
• Square root of 5: √5 ≈ 2.24;
• Square root of 7: √7 ≈ 2.65;
• Square root of 11: √11 ≈ 3.32;
• Square root of 13: √13 ≈ 3.61;
• Square root of 17: √17 ≈ 4.12;
• Square root of 19: √19 ≈ 4.34; etc.

Let's try and find the square root of 52 again. You can simplify it to √52 = 2√13 (you will learn how to simplify square roots in the next section) and then substitute √13 ≈ 3.61. Finally, make a multiplication √52 ≈ 2 × 3.61 = 7.22. The result is the same as before!

In some situations, you don't need to know the exact value of the square root. If this is the case, our square root calculator is the best option to estimate the value of every square root you desire. For example, let's say you want to know whether 4√5 is greater than 9. From the calculator, you know that √5 ≈ 2.23607, so 4√5 ≈ 4 × 2.23607 = 8.94428. It is very close to 9, but it isn't greater than it! The square root calculator gives the final value with relatively high accuracy (to five digits in the above example).

Remember that our calculator automatically recalculates numbers entered into either of the fields. You can find the square root of a specific number by filling the first window or getting the square of a number that you entered in the second window. The second option is handy in finding perfect squares that are essential in many aspects of math and science. For example, if you enter 17 in the second field, you will find out that 289 is a perfect square.

In some applications, particularly in experimental sciences such as chemistry and physics, the results are preferred in scientific notation. In brief, an answer in scientific notation must have a decimal point between the first two non-zero numbers. It will be represented as the decimal multiplied by 10 raised to an exponent. For example, the number 0.00345 is written as 3.45 × 10⁻³ in scientific notation, whereas 145.67 is written as 1.4567 × 10² in scientific notation. The results obtained using the square root calculator can be converted to scientific notation with the scientific notation calculator.

The same number can often be presented as a square root in multiple ways. For instance, √8 = 2√2 and √9 = 3. Obviously, writing 3 as 3 is much simpler than presenting it as √9. We extend this idea to other roots — we consider a form of a root simpler if the radicand (the number under the root) is as small as possible. By this logic, we tend to think of 2√2 as being a "simpler" expression than √8, even though both numbers are the same.

To "simplify" a root √x, therefore, means to write it in the form a√b, where a and b are whole numbers and b is as small as possible. Simplifying roots will come in handy while adding and subtracting roots — check out the next section for more!

But why exactly are √8 and 2√2 the same numbers? This is because roots satisfy the property:

√(x × y) = √x × √y

In words, multiplying two numbers first and then taking their roots gives the same result as taking roots first and multiplying them afterward. To convince yourself that this useful identity holds, simply square both sides and note that both √(x × y) and √x × √y are non-negative square roots of x × y. Then recall that a number can have at most one non-negative square root, and so √(x × y) and √x × √y must be equal!

Using this handy formula, we can show that indeed:

√8 = √(4 × 2) = √4 × √2 = 2√2

When can you simplify a root? To answer this question, we need to find the factors of the radicand. Suppose that the radicand has a perfect square factor, i.e., 4, 9, 16, 25, 36, 49, 64, and so on (these numbers can be respectively expressed as 2², 3², 4², 5², 6², 7², hence the name). Then, you can simplify the square root by following these steps:

1. Write down the radicand as a product of a perfect square and another number: in our case, this would be 8 = 4 × 2 because 4 = 2² is a perfect square.
2. Use the handy identity above to express a root of the product as the product of roots: √(4 × 2) = √4 × √2.
3. Take the square root of the perfect square: √4 = 2.

By combining these steps, we get √8 = 2√2 as we wanted! Let's take a look at more examples:

• Can you simplify √27? The factors of 27 are 1, 3, 9, 27. There is a 9 here, which is a perfect square! This means that you can simplify √27. What does this root look like in the simplified form?

• How about √15? Factors of 15 are 1, 3, 5, and 15. None of them is a perfect square, so this square root can't be simplified.

What is the main takeaway of this discussion? You can simplify a square root precisely if it contains a perfect square among its factors.

Let's practice simplifying square roots with a few more examples:

• How to simplify the square root of 27?

  √27 = √(9 × 3) = √9 × √3 = 3√3

• How to simplify the square root of 45?

  √45 = √(9 × 5) = √9 × √5 = 3√5

• How to simplify the square root of 144?

  √144 = √(4 × 36) = √4 × √36 = 2 × 6 = 12

Note that in the last example, you don't have to factor 144 into 4 and 36. If you remember that 144 = 12 × 12 is a perfect square, you can directly simplify √144 to 12. But if you don't remember large perfect squares off the top of your head, then the easiest way to proceed is to identify small perfect squares among factors of 144 (as we did, showing that 4 divides 144) and factor 144 into smaller perfect squares first.

How about higher-degree roots, e.g., a cube root? They can be simplified similarly to square roots. The main difference is that to simplify a cube root, you need to find at least one factor that is a perfect cube, not a perfect square, i.e., 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³, and so on. Then, you proceed analogously, starting with factoring your number into a perfect cube and another number. For instance, ³√192 can be simplified as follows:

∛192 = ∛(64 × 3) = ∛64 × ∛3 = 4∛3

Simplifying cube roots may seem a bit complicated at first glance, but after some practice, you will be able to simplify the roots in your head. Trust us!

Adding and subtracting square roots

Unfortunately, adding and subtracting square roots is not as easy as adding/subtracting regular numbers. For example, if 2 + 3 = 5, it doesn't mean that √2 + √3 equals √5. That's wrong! To understand why that is, imagine that you have two different types of shapes: triangles 🔺 and circles 🔵. What happens when you add one triangle to one circle 🔺 + 🔵? Nothing! You still have one triangle and one circle 🔺 + 🔵. On the other hand, what happens when you try to add three triangles to five triangles: 3🔺 + 5🔺? You'll end up with eight triangles 8🔺.

Adding square roots is very similar to this. The result of adding √2 + √3 is still √2 + √3. You can't simplify it further. It is different, however, when both square roots have the same number under the root symbol. Then, we can add them just like we added triangles before. For example, 3√2 + 5√2 equals 8√2. The same is true for subtracting square roots: 3√2 - 5√2 equals -2√2. Let's take a look at more examples illustrating this square root property:

• What is 6√17 + 5√17? Answer: 6√17 + 5√17 = 11√17;

• What is 4√7 - 7√7? Answer: 4√7 - 7√7 = -3√7;

• What is 2√2 + 3√8? Answer: 2√2 + 3√8 = 2√2 + 6√2 = 8√2, because we simplified √8 = √(4 × 2) = √4 × √2 = 2√2;

• What is √45 - √20? Answer: √45 - √20 = 3√5 - 2√5 = √5, because we simplified √45 = √(9 × 5) = √9 × √5 = 3√5 and √20 = √(4 × 5) = √4 × √5 = 2√5;

• What is 7√13 + 2√22? Answer: 7√13 + 2√22, we can't simplify this further;

• What is √3 - √18? Answer: √3 - √18 = √3 - 3√2, we can't simplify this further than this, but we at least simplified √18 = √(9 × 2) = √9 × √2 = 3√2.

Multiplying and dividing square roots

Now, when adding square roots is a piece of cake for you, let's go one step further. What about multiplying square roots and dividing square roots? Don't be scared! In fact, you already did it during the lesson on simplifying square roots. Multiplying square roots is the same as taking the square root of the product:

√(x × y) = √x × √y

We explained where this comes from in the section on simplifying square roots. Here, we will justify this identity from a different angle. Recall the square root property that we have already used several times:

√x = x^1/2

Do you remember how to multiply numbers that are raised to the same power? As a reminder:

xⁿ × yⁿ = (x × y)ⁿ

Taking n = 1/2, we see that:

x^1/2 × y^1/2 = (x × y)^1/2

which is an alternative phrasing of

√x × √y = √(x × y)!

As opposed to addition, you can multiply every two square roots. Remember that multiplication is commutative: this fancy word means that numbers can be multiplied in any order. Here is how we use this fact:

• What is √3 × √2? Answer: √3 × √2 = √6.

• What is 2√5 × 5√3? Answer: 2√5 × 5√3 = 2 × 5 × √5 × √3 = 10√15, because multiplication is commutative.

• What is 2√6 × 3√3? Answer: 2√6 × 3√3 = 2 × 3 × √6 × √3 = 6√18 = 18√2, we simplified √18 = √(9 × 2) = √9 × √2 = 3√2.

How about dividing square roots? You are lucky; the division of roots satisfies a similar formula to multiplication:

√x / √y = √(x / y)

All you need to do is to replace the multiplication sign with a division. In words: it doesn't matter if we first divide or first take the roots, the end result will be the same. Just like with multiplication, this is a special case (with n = 1/2) of the formula for the division of powers:

xⁿ / yⁿ = (x / y)ⁿ

However, division is not commutative! You have to calculate the numbers that stand before the square roots and the numbers under the square roots separately. As always, here are some practical examples:

• What is √15 / √3? Answer: √15 / √3 = √5.

• What is 10√6 / 5√2? Answer: 10√6 / 5√2 = (10 / 5) × (√6 / √2) = 2√3;

• What is 6√2 / 3√5? Answer: 6√2 / 3√5 = (6 / 3) × (√2 / √5) = 2√(2/5).

  In this form, the answer looks a bit odd: we typically prefer a whole number as radicand. This can be achieved with a few more lines of computations: 2√(2/5) = (2/5) × (5√(2/5)) = (2/5) × (√(25 × 2/5)) = (2/5) √10. In words, the result is two-fifths of the square root of 10.

Calculating the square root of powers and fractions might not be clear to you. But with the knowledge you acquired in the previous section, you should find it easier than expected! Let's begin with the square roots of powers. In that case, it will be easier for you to use the alternative form of square root √x = x^1/2. Do you remember the power rule? If not, here is a quick reminder:

(xⁿ)^m = x^{n × m}

where n and m are any real numbers. Now, when you place 1/2 instead of m, you'll get nothing else but a fraction as the exponent:

√(xⁿ) = (xⁿ)^1/2 = x^n/2

That's how you find the square root of a power! Speaking of powers, the above equation looks very similar to the standard normal distribution density function, which is widely used in statistics.

If you're still not sure about taking square roots of powers, here are a few more examples:

• Square root of 2⁴:

  √(2⁴) = (2⁴)^1/2 = 2^4/2 = 2² = 4

• Square root of 5³:

  √(5³) = (5³)^1/2 = 5^3/2

• Square root of 4⁵:

  √(4⁵) = (4⁵)^1/2 = 4^5/2 = (2²)^5/2 = 2⁵ = 32

As you can see, sometimes it is impossible to get a pretty result like in the first example. However, in the third example, we showed you a little trick with expressing 4 as 2². This approach can often simplify more complicated equations.

What about square roots of fractions? Take a look at the previous section where we wrote about dividing square roots. You can find there the following relation that should explain everything:

(x / y)^1/2 ⟺ √x / √y = √(x / y)

where x / y is a fraction. Below, you can find some examples of square roots of a fraction:

• Square root of 4/9:

  √(4/9) = √4 / √9 = 2/3

• Square root of 1/100:

  √(1/100) = √1 / √100 = 1/10

• Square root of 1/5:

  √(1/5) = √1 / √5 = 1/√5 = √5/5

Leaving roots in the denominator is not a very good habit: it is easier to add or subtract numbers later on if their roots are in the numerator. That's why we got rid of it in the last example. We just multiplied both the numerator and denominator by the same number (we can always do that, as the number we multiply by equals 1), in this case, by √5.

Functions play a vital role not only in mathematics but in many other areas like physics, statistics, or finance. Function f(x) is nothing more than a formula that says how the value of f(x) changes with the argument x. Below you can find the graph of the square root function f(x) = √x, made up of a half of the parabola. Check it and try to validate, for example, whether the square root function of x = 9 is 3 and of x = 16 is 4 (as it should be).

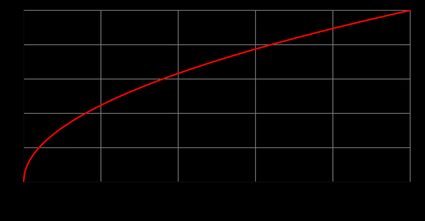
Let's go back to the square root function f(x) = √x and explore its basic properties. We consider there only the positive part of f(x) (as you can see in the square root graph above). So, the square root function:

• Is continuous and growing for all non-negative x;

• Is differentiable for all positive x (see the derivative of the square root section for more information);

• Goes to infinity as x goes to infinity (lim √x → ∞ when x → ∞); and

• Is a real number for all non-negative x.

A derivative of a function tells us how fast this function changes with its argument. One of the simplest examples in physics is the position of an object and its velocity (the rate of change of position). Let's say that the function x(t) describes how the distance of the moving car from a specific point changes with time t. Do you know what determines how fast the traveled distance changes? The answer is the speed of the car! So the derivative of the position x(t) is velocity v(t)(velocity can depend on time too). To denote the derivative, we usually use the apostrophe v(t) = x'(t) or the derivative symbol v(t) = dx(t)/dt.

The derivative of a general function f(x) is not always easy to calculate. However, for some specific functions, we've got some nice formulas. For example, if

f(x) = xⁿ

where n is any real number, the derivative is as follows:

f'(x) = n × x^(n-1)

It may not look like it, but this answers the question what is the derivative of a square root. Do you remember the alternative (exponential) form of a square root? Let us remind you:

√x = x^1/2

You can see that in this case, n = 1/2, so the derivative of a square root is:

(√x)' = (x^1/2)' = 1/2 × x^-1/2 = 1/(2√x)

Since a negative power of a number is one over that number, the estimation of the derivative will involve fractions. We've got a tool that could be essential when adding or subtracting fractions with different denominators. It is called the LCM calculator, and it tells you how to find the Least Common Multiple.

The derivative of a square root is needed to obtain the coefficients in the so-called Taylor expansion. We don't want to dive into details too deeply, so briefly, the Taylor series allows you to approximate various functions with the polynomials that are much easier to calculate. For example, the Taylor expansion of √(1 + x) about the point x = 0 is given by:

√(1 + x) = 1 + 1/2 × x - 1/8 × x² + 1/16 × x³ - 5/128 × x⁴ + ...

which is valid for -1 ≤ x ≤ 1. Although the above expression has an infinite number of terms, to get the approximate value, you can use just the first few terms. Let's try it! With x = 0.5 and the first five terms, you get:

√(1.5) = 1 + 1/2 × 0.5 - 1/8 × 0.25 + 1/16 × 0.125 - 5/128 × 0.0625

√(1.5) ≈ 1.2241

and the real value, provided by our calculator, is √(1.5) ≈ 1.2247. Close enough!

That was a lot of maths and equations so far. For those of you who are persistent enough, we've prepared the next section, which explains how to calculate the square root of a negative number.

At school, you have probably been taught that the square root of a negative number does not exist. This is true when you consider only real numbers. A long time ago, to perform advanced calculations, mathematicians had to introduce a more general set of numbers – the complex numbers. They can be expressed in the following form:

x = a + b i

where x is the complex number with the real part a and the imaginary part b. What differs between a complex number and a real one is the imaginary number i. Here you have some examples of complex numbers: 2 + 3i, 5i, 1.5 + 4i, and 2. You may be surprised to see 2 there, which is a real number. Yes, it is, but it is also a complex number with b = 0. Complex numbers are a generalization of real numbers.

So far, the imaginary number i is probably still a mystery for you. What is it at all? Well, although it may look weird, it is defined by the following equation:

i = √(-1)

and that's all that you need to calculate the square root of every number, whether it is positive or not. Let's see some examples:

• Square root of -9: √(-9) = √(-1 × 9) = √(-1)√9 = 3i;
• Square root of -13: √(-13) = √(-1 × 13) = √(-1)√13 = i√13; and
• Square root of -49: √(-49) = √(-1 × 49) = √(-1)√49 = 7i.

Isn't that simple? This problem doesn't arise with the cube root since you can obtain the negative number by multiplying three of the identical negative numbers (which you can't do with two negative numbers). For example:

³√(-64) = ³√[(-4)×(-4)×(-4)] = -4

And that's all you need to know about square roots!