Kalkulator wartości p

Witamy w Omni kalkulatorze wartości p. Nigdy więcej nie będziesz już musiał(a) kłopotać się wyznaczaniem wartości p (p-wartości, ang. p-value), ponieważ nasze narzędzie przeliczy za ciebie wartość statystyki testowej na jednostronne i dwustronne wartości p dla wszystkich najpopularniejszych rozkładów: normalnego, t-Studenta, chi-kwadrat i F-Snedecora.

Choć wartość p pojawia się w najróżniejszych dziedzinach nauki, dla wielu osób to pojęcie wciąż jest nieco onieśmielające. Nie przejmuj się — w poniższym artykule wyjaśnimy nie tylko, czym w teorii jest wartość p, ale także jak poprawnie ją interpretować. Czy kiedykolwiek zastanawiało cię, jak ręcznie obliczać wartość p? Zaraz zobaczysz wszystkie niezbędne wzory!

Formalnie, wartość p jest prawdopodobieństwem tego, że statystyka testowa przyjmie wartości co najmniej tak skrajne, jak wartość, którą przyjęła dla twojej próbki. Należy pamiętać, że prawdopodobieństwo to jest obliczane przy założeniu prawdziwości hipotezy zerowej H₀!

Oznacza to, że wartość p odpowiada na następujące pytanie:

Zakładając, że żyjemy w świecie, w którym hipoteza zerowa jest prawdziwa, jak prawdopodobne jest, że test, który właśnie przeprowadzamy, wygeneruje dla nowej próbki wartość co najmniej tak skrajną jak ta, którą dostaliśmy dla dotychczasowej próbki?

Co oznacza skrajna wartość? Otóż określa to hipoteza alternatywna, zatem wartość p zależy też od rozważanej przez nas hipotezy alternatywnej: lewostronnej, prawostronnej lub dwustronnej. W poniższych wzorach S oznacza statystykę testową, x oznacza jej wartość uzyskaną dla danej próby, a Pr(zdarzenie | H₀) to prawdopodobieństwo zdarzenia, obliczone przy założeniu, że H₀ jest prawdziwa:

1. Test lewostronny: p-wartość = Pr(S ≤ x | H₀)

2. Test prawostronny: p-wartość = Pr(S ≥ x | H₀)

3. Test dwustronny:

   p-wartość = 2 · min{Pr(S ≤ x | H₀), Pr(S ≥ x | H₀)}

   (min{a,b} oznacza mniejszą spośród liczb a i b)

   Jeśli rozkład statystyki testowej przy założeniu prawdziwości H₀ jest symetryczny względem 0, to:
   p-wartość = 2 · Pr(S ≥ |x| | H₀)

   lub, równoważnie:
   p-wartość = 2 · Pr(S ≤ -|x| | H₀)

Rysunek wyjaśnia więcej niż tysiąc słów; postaramy się więc teraz zilustrować te definicje. Wykorzystamy fakt, że prawdopodobieństwo można zgrabnie przedstawić jako obszar pod krzywą gęstości danego rozkładu. Pokażemy dwa zestawy rysunków: jeden dla rozkładu symetrycznego, a drugi dla rozkładu skośnego (niesymetrycznego).

• Przypadek symetryczny: rozkład normalny:

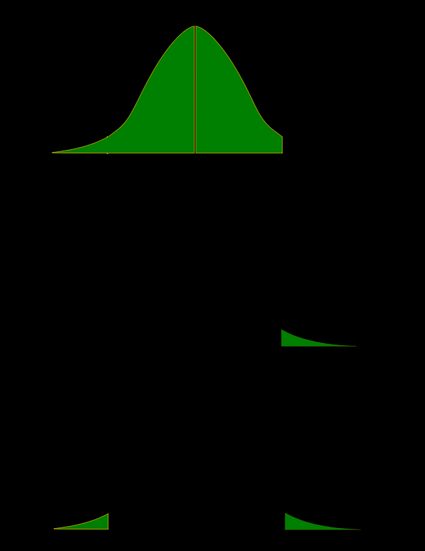
• Przypadek niesymetryczny: rozkład chi-kwadrat:

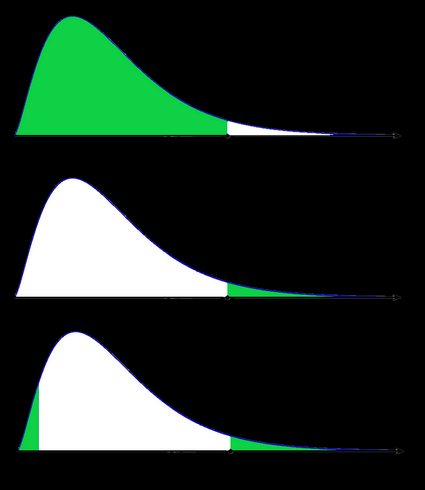
Na ostatnim rysunku (dwustronna wartość p dla rozkładu skośnego), zaznaczone pole pod krzywą po lewej stronie jest równe zaznaczonemu polu pod krzywą po prawej stronie.

Aby określić wartość p, trzeba znać rozkład statystyki testowej przy założeniu, że hipoteza zerowa jest prawdziwa. Następnie, za pomocą dystrybuanty tego rozkładu (cdf, ang. cummulative distribution function) możemy wyrazić prawdopodobieństwo tego, że statystyka testowa przyjmie wartości co najmniej tak skrajne jak wartość x, którą przyjęła dla badanej próby:

1. Test lewostronny:

   p-wartość = cdf(x).

2. Test prawostronny:

   p-wartość = 1 - cdf(x).

3. Test dwustronny:

   p-wartość = 2 · min{cdf(x) , 1 - cdf(x)}.

   Jeśli rozkład statystyki testowej (pod warunkiem prawdziwości H₀) jest symetryczny względem 0, to wzór na dwustronną wartość p można uprościć do postaci p-wartość = 2 · cdf(-|x|), lub, równoważnie, p-wartość = 2 - 2 · cdf(|x|).

Najbardziej rozpowszechnione w testowaniu hipotez rozkłady prawdopodobieństwa mają bardzo skomplikowane wzory na dystrybuantę i ręczne znalezienie wartości p najczęściej nie jest możliwe. Prawdopodobnie będziesz musiał(a) skorzystać z komputera lub tablic statystycznych, w których zebrano przybliżone wartości dystrybuant.

Wiesz już, jak obliczać wartość p, ale... po co w ogóle obliczać tę wielkość? W testowaniu hipotez obliczenie wartości p jest alternatywą dla obliczania wartości krytycznej. Przypomnijmy, że to drugie podejście wymaga od badacza wstępnego ustalenia poziomu istotności, α, który jest prawdopodobieństwem odrzucenia hipotezy zerowej gdy jest ona prawdziwa (a więc prawdopodobieństwo błędu I rodzaju). Natomiast po obliczeniu wartości p możesz porównać ją z dowolnym α, aby szybko zdecydować, czy na wybranym poziomie istotności należy odrzucić hipotezę zerową. Aby uzyskać szczegółowe informacje, przeczytaj następną sekcję — wyjaśnimy w niej, jak należy interpretować wartość p.

Jak wspomnieliśmy wyżej, wartość p odpowiada na następujące pytanie:

Zakładając, że żyjemy w świecie, w którym hipoteza zerowa jest prawdziwa, jak prawdopodobne jest, że statystyka testowa przyjmie dla innej próbki wartość co najmniej tak ekstremalną jak ta, którą uzyskaliśmy dla badanej właśnie próbki?

Co to oznacza? Otóż są dwie możliwości:

• Wysoka wartość p oznacza, że twoja próbka jest zgodna z hipotezą zerową; oraz
• Mała wartość p dostarcza dowodów przeciwko hipotezie zerowej, ponieważ oznacza ona, że uzyskany wynik byłby bardzo mało prawdopodobny, gdyby hipoteza zerowa była prawdziwa.

Może się jednak zdarzyć, że hipoteza zerowa jest prawdziwa, ale próba jest bardzo nietypowa! Na przykład, wyobraźmy sobie, że badaliśmy wpływ nowego leku i uzyskaliśmy wartość p równą 0,03. Oznacza to, że nawet gdyby lek nie miał żadnego rzeczywistego wpływu na zdrowie pacjenta, to w 3% analogicznych badań otrzymalibyśmy tę samą lub jeszcze większą wartość statystyki testowej, jedynie przez czysty przypadek!

Na pytanie „co to jest wartość p” można również odpowiedzieć w następujący sposób: wartość p to najmniejszy poziom istotności, przy którym hipoteza zerowa zostałaby odrzucona. Tak więc, jeśli chcesz podjąć decyzję o ewentualnym odrzuceniu hipotezy zerowej na pewnym poziomie istotności α, musisz porównać wartość p z wybranym poziomem α:

• Jeśli p-wartość ≤ α, to odrzucasz hipotezę zerową i przyjmujesz hipotezę alternatywną;
• Jeśli p-wartość ≥ α, to nie masz wystarczających dowodów, aby odrzucić prawdziwość hipotezy zerowej.

Oczywiście los hipotezy zerowej zależy od α. Na przykład, jeśli wartość p wynosiła 0,03, odrzucilibyśmy hipotezę zerową na poziomie istotności 0,05, ale na poziomie 0,01 już nie. Właśnie dlatego poziom istotności powinien być ustalony z góry, a nie dostosowywany już po wyliczeniu wartości p! Poziom istotności 0,05 jest najczęściej spotykany, ale pamiętaj, że nie ma w nim nic magicznego. Tutaj możesz zobaczyć, do czego prowadzi zbyt silna wiara w próg 0,05. Najlepiej jest podać wartość p i pozwolić czytelnikowi na wyciągnięcie własnych wniosków.

Należy również pamiętać, że kluczowe znaczenie ma wiedza i doświadczenie badacza w danej dziedzinie (i zdrowy rozsądek). Bezmyślne stosowanie praw statystyki może doprowadzić cię do wniosków statystycznie istotnych, ale całkowicie nieprawdziwych.

Nasz kalkulator wartości p jest do twojej dyspozycji, więc nie musisz już wyliczać wartości p przy użyciu tych wszystkich skomplikowanych wzorów! Wystarczy, że wykonasz następujące kroki:

1. Wybierz hipotezę alternatywną: dwustronną, prawostronną lub lewostronną.

2. Podaj rozkład statystyki testowej dla hipotezy zerowej: czy jest to rozkład N(0,1), t-Studenta, chi-kwadrat, czy F-Snedecora? Nie masz pewności? Czytaj dalej, kolejne sekcje są poświęcone poszczególnym rozkładom.

3. W razie potrzeby określ liczbę stopni swobody rozkładu statystyki testowej.

4. Wprowadź wartość statystyki testowej dla twojej próbki danych.

5. Nasz kalkulator wylicza wartość p na podstawie statystyki testowej i podaje decyzję, którą należy podjąć w odniesieniu do hipotezy zerowej. Domyślnie, poziom istotności wynosi 0,05.

Przejdź do trybu zaawansowanego (Advanced mode) jeśli chcesz zmienić poziom istotności lub zwiększyć precyzję, z jaką wykonywane są obliczenia.

Przy użyciu dystrybuanty standardowego rozkładu normalnego, która jest tradycyjnie oznaczana literą Φ, wartość p możemy obliczyć na podstawie wartości Z (Z-score) za pomocą następujących wzorów:

1. Lewostronny test Z:

   p-wartość = Φ(Z_score)

2. Prawostronny test Z:

   p-wartość = 1 - Φ(Z_score)

3. Dwustronny test Z:

   p-wartość = 2 · Φ(-|Z_score|)

   lub

   p-wartość = 2 - 2 · Φ(|Z_score|)

Wartości Z używamy, gdy rozkład statystyki testowej jest (przynajmniej w przybliżeniu) zgodny ze standardowym rozkładem normalnym N(0,1). Dzięki centralnemu twierdzeniu granicznemu możesz używać wartości Z jeśli masz dużą próbkę (co najmniej 50 punktów danych).

Test Z najczęściej odnosi się do testowania średniej populacji lub różnicy między średnimi dwóch populacji (na przykład między dwiema proporcjami). Testy Z można również spotkać w metodzie największej wiarygodności.

Aby wyliczyć wartość p na podstawie t-score (czyli wartości statystyki testowej o rozkładzie t-Studenta), użyj następujących wzorów. Przez cdf_t,d oznaczamy dystrybuantę rozkładu t-Studenta o d stopniach swobody:

1. Lewostronny test t:

   p-wartość = cdf_t,d(t_score)

2. Prawostronny test t:

   p-wartość = 1 - cdf_t,d(t_score)

3. Dwustronny test t:

   p-wartość = 2 · cdf_t,d(-|t_score|)

   lub

   p-wartość = 2 - 2 · cdf_t,d(|t_score|)

Użyj testu t, gdy statystyka testowa ma rozkład t-Studenta. Rozkład ten ma kształt podobny do rozkładu normalnego N(0,1) (krzywa dzwonowa), ale ma cięższe ogony (tzn. wartości krańcowe są bardziej prawdopodobne niż w N(0,1)) — dokładny kształt rozkładu t-Studenta zależy od parametru zwanego stopniami swobody. Jeśli liczba stopni swobody jest duża (>30), co zwykle ma miejsce w przypadku dużych próbek, to rozkład t-Studenta jest w praktyce nieodróżnialny od N(0,1).

Najpopularniejsze testy t badają średnią populacji o nieznanym odchyleniu standardowym lub też różnicę średnich dla dwóch populacji z nieznanymi (równymi lub różnymi) odchyleniami standardowymi. Istnieje również test t dla sparowanych (zależnych) próbek.

Użyj opcji test χ² gdy wykonujesz test, w którym statystyka testowa ma rozkład chi-kwadrat.

Rozkład ten ma np. suma kwadratów zmiennych losowych, z których każda ma rozkład normalny N(0,1). Pamiętaj, aby sprawdzić liczbę stopni swobody rozkładu χ² twojej statystyki testowej!

Jak znaleźć wartość p znając χ²-score? Można to zrobić za pomocą poniższych wzorów, w których cdf_χ²,d oznacza dystrybuantę rozkładu χ² o d stopniach swobody:

1. Lewostronny test χ²:

   p-wartość = cdf_χ²,d(χ²_score)

2. Prawostronny test χ²:

   p-wartość = 1 - cdf_χ²,d(χ²_score)

   Pamiętaj, że testy χ² zgodności i niezależność są testami prawostronnymi! (zob. niżej)

3. Dwustronny test χ²:
   p-wartość = 2 · min{cdf_χ²,d(χ²_score), 1 - cdf_χ²,d(χ²_score)}

   (min{a,b} oznacza mniejszą z liczb a i b)

Najpopularniejsze testy prowadzące do otrzymania χ²-score to:

• Testowanie, czy wariancja danych z rozkładu normalnego ma pewną z góry określoną wartość. W tym przypadku statystyka testowa ma rozkład χ² o n - 1 stopniach swobody, gdzie n jest wielkością próby. Może to być test jednostronny lub dwustronny.

• Test zgodności rozkładów (dopasowania) sprawdza, czy rozkład empiryczny (próby) zgadza się z pewnym oczekiwanym rozkładem prawdopodobieństwa. W tym przypadku statystyka testowa ma rozkład χ² o k - 1 stopniach swobody, gdzie k jest liczbą klas, na które podzielona jest próba. Jest to test prawostronny.

• Test niezależności służy do określenia, czy istnieje statystycznie istotny związek między dwiema zmiennymi. Statystyka testowa opiera się na tabeli krzyżowej i ma rozkład χ² o (r - 1)(c - 1) stopniach swobody, gdzie r to liczba wierszy, a c to liczba kolumn w tabeli krzyżowej. Jest to test prawostronny.

Wreszcie, opcja wartości F powinna być używana podczas wykonywania testu, w którym statystyka testowa jest zgodna z rozkładem F, znanym również jako rozkład Fishera-Snedecora. Dokładny kształt rozkładu F zależy od dwóch typów stopni swobody.

Aby zobaczyć, skąd pochodzą te stopnie swobody, rozważmy niezależne zmienne losowe X i Y, które obie mają rozkład χ² z odpowiednio d₁ i d₂ stopniami swobody. W takim przypadku stosunek (X/d₁)/(Y/d₂) jest zgodny z rozkładem F, z (d₁, d₂) stopniami swobody. Z tego powodu dwa parametry d₁ i d₂ są również nazywane licznikiem i mianownikiem stopni swobody.

Wartość p z wyniku F jest określona przez następujące wzory, gdzie cdf_F,d1,d2 oznacza funkcję skumulowanego rozkładu rozkładu F, z (d₁, d₂) stopniami swobody:

1. Lewostronny test F:

   p-wartość = cdf_F,d1,d2(F_score)

2. Prawostronny test F:

   p-wartość = 1 - cdf_F,d1,d2(F_score)

3. Dwustronny test F:

   p-wartość = 2 · min{cdf_F,d1,d2(F_score), 1 - cdf_F,d1,d2(F_score)}

   (Przez min{a,b} oznaczamy mniejszą z liczb a i b)

Poniżej wymieniamy najważniejsze testy, które dają wyniki F. Wszystkie z nich są testami prawostronnymi.

• Test na równość wariancji w dwóch populacjach o rozkładzie normalnym. Jego statystyka testowa jest zgodna z rozkładem F z (n - 1, m - 1) stopniami swobody, gdzie n i m są odpowiednimi rozmiarami próbek.

• ANOVA jest używana do testowania równości średnich w trzech lub więcej grupach, które pochodzą z normalnie rozłożonych populacji o równych wariancjach. Otrzymujemy rozkład F z (k - 1, n - k) stopniami swobody, gdzie k to liczba grup, a n to całkowita wielkość próby (we wszystkich grupach razem).

• Test na ogólną istotność analizy regresji. Statystyka testowa ma rozkład F z (k - 1, n - k) stopniami swobody, gdzie n jest wielkością próby, a k jest liczbą zmiennych (wliczając wyraz wolny).

  Po potwierdzeniu zależności liniowej w próbce danych za pomocą powyższego testu, można obliczyć współczynnik determinacji, R², który wskazuje siłę tej zależności. Można to zrobić ręcznie lub skorzystać z naszego kalkulatora współczynnika determinacji 🇺🇸.

• Test do porównania dwóch zagnieżdżonych modeli regresji. Statystyka testowa jest zgodna z rozkładem F z (k₂ - k₁, n - k₂) stopniami swobody, gdzie k₁ i k₂ to liczba zmiennych odpowiednio w mniejszym i większym modelu, a n to wielkość próby.

  Można zauważyć, że test F ogólnej istotności jest szczególną formą testu F do porównywania dwóch modeli zagnieżdżonych: testuje on, czy nasz model radzi sobie istotnie lepiej niż model bez zmiennych objaśniających (tj. model zawierający tylko wraz wolny).

Nie, wartość p nie może być ujemna. Wynika to z faktu, że prawdopodobieństwa nie mogą być ujemne, a wartość p jest prawdopodobieństwem tego, że statystyka testowa spełnia pewne określone warunki.

Duża p-wartość (p-value) oznacza, że przy założeniu prawdziwości hipotezy zerowej jest bardzo prawdopodobne, że dla innej próbki statystyka testowa wygeneruje wartość co najmniej tak skrajną, jak ta uzyskana dla badanej próbki. Wysoka p-wartość nie pozwala na odrzucenie hipotezy zerowej.

Mała p-wartość (p-value) oznacza, że przy założeniu prawdziwości hipotezy zerowej jest mało prawdopodobne, że dla innej próbki statystyka testowa przyjmie wartość co najmniej tak skrajną, jak ta zaobserwowana dla badanej próbki. Mała p-wartość przemawia na korzyść hipotezy alternatywnej — pozwala odrzucić hipotezę zerową i przyjąć hipotezę alternatywną.