Zuletzt aktualisiert: 21. Oct 2024

Kreisfläche Rechner

Q: Wie groß ist der Radius eines Kreises mit Flächeninhalt 10?

Der Radius beträgt 1,784 . Die genaue Antwort lautet √(10 / π) . Um dieses Ergebnis zu erhalten, erinnere dich an die Formel Fläche = π ∙ r 2 . Wir wandeln sie in die Form r 2 = Fläche / π um und sehen, dass der Radius gleich der Quadratwurzel von Fläche / π ist. Wenn wir Fläche = 10 einsetzen, erhalten wir: Radius = √(10 / π) ≈ √(10 / 3,14) ≈ √3,185 ≈ 1,785 .

Q: Wie finde ich den Umfang eines Kreises bei gegebener Fläche?

Um den Umfang eines Kreises aus seiner Fläche zu bestimmen, gehe folgendermaßen vor: Multipliziere den Flächeninhalt mit π. Ziehe die Quadratwurzel aus dem Ergebnis von Schritt 1. Multipliziere mit 2. Du hast den Umfang des Kreises aus seinem Flächeninhalt ermittelt! Gut gemacht!

Q: Können die Fläche und der Umfang eines Kreises gleich sein?

Ja , die Fläche und der Umfang eines Kreises haben den gleichen Wert 4π , wenn der Radius des Kreises die Länge 2 hat. Bedenke aber, dass die Einheiten unterschiedlich sind! Der Umfang wird in Längeneinheiten , und der Flächeninhalt, nun ja, in Flächeneinheiten ausgedrückt.

Q: Können die Fläche und der Radius eines Kreises gleich sein?

Ja , nimm einen Kreis mit Radius r = 1/π . Dann ist sein Flächeninhalt gleich πr 2 = π(1/π) 2 = 1/π , er hat also denselben Wert wie der Radius. Beachte jedoch, dass sich die Einheiten unterscheiden ! Der Radius und der Flächeninhalt werden in Einheiten für die Länge bzw. Fläche ausgedrückt; zum Beispiel in cm und in cm 2 .

Erstellt von Łucja Zaborowska, promovierende*r Mediziner*in

Überprüft von Dominik Czernia, Doktorand*in

Dominik Czernia

PhD, Institute of Nuclear Physics PAN

LinkedInWebsiteResearch Gate

Physicist at the Institute of Nuclear Physics in Kraków interested in magnetism and always ready to explain everything to everyone in simple terms. He is currently working on adding more scientific papers to his collection, accompanied by his son and another baby on its way. A perfectionist with an acute eye for detail, he has a unit converter in his brain and uses it to compare prices at the supermarket. Loves peace and quiet, especially during hiking. See full profile

Check our editorial policy

und Jack Bowater

Übersetzt von Luise Schwenke

Luise Schwenke

Luise works as a German translator and Calculatorian at Omni. She holds a degree in Food Engineering from the University of Sciences - Neubrandenburg, Germany, and specialized her career in biotechnology. She worked in human genetic diagnostics, developing and producing pharmaceutical products for clinical phase 2 and 3 studies. She is always hungry for new fields to learn about that allow her to combine her creative and analytical thinking. Currently, she is getting her hands on coding, focusing on data science and big data. Luise spent an academic year in Brazil and loves traveling the world to experience and learn from different cultures. See full profile

Check our editorial policy

und Marcelina Wiśniewska

Neu

Inhalt

Kreis — Flächeninhalt Formel Wie wird unser Kreisfläche Rechner verwendet? Durchmesser zu Fläche und Radius zu Fläche.Wozu berechnen wir den Flächeninhalt eines Kreises?FAQs

Der Kreisfläche Rechner hilft dir dabei, die Kreisfläche mit dem Durchmessers oder Radius zu berechnen. Unser Kreisfläche Rechner funktioniert in beide Richtungen — egal, ob du die Fläche aus dem Radius oder den Radius aus der Fläche suchst, du bist hier genau richtig ◔

Wir geben dir einen Überblick über die wichtigsten Informationen zum Flächeninhalt eines Kreises, seinem Durchmesser und seinem Radius. Wir schauen uns an, wie wir die Kreisfläche berechnen und welche Formel dafür verwendet wird. Zudem schauen wir uns Beispiele anderer mathematischer Gebiete an, in denen dieselbe Gleichung angewendet wird.

Kreis — Flächeninhalt Formel

Schauen wir uns also an, wie der Flächeninhalt eines Kreises bestimmt wird. Du kannst die Berechnung mithilfe des Durchmessers oder des Radius durchführen.

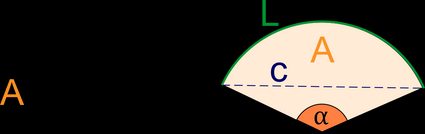
💡 Der Durchmesser ist die Strecke, die die Mitte des Kreises kreuzt und die beiden Ränder berührt. Der Radius beginnt in der Mitte des Kreises und endet an seinem Rand.

Du kannst den Durchmesser eines Kreises ermitteln, indem du den Radius des Kreises mal zwei multiplizierst:

Durchmesser = 2 ∙ Radius

Kreis — Flächeninhalt Formel:

Fläche eines Kreises = π ∙ r²

Um die Kreisfläche mit dem Durchmesser zu berechnen, benutze die folgende Gleichung:

Fläche eines Kreises = π ∙ (d/2)²

wobei:

π gerundet 3,14 entspricht. Es spielt keine Rolle, ob du die Kreisfläche mit dem Durchmesser oder dem Radius bestimmen willst — du wirst diese Konstante in fast jedem Fall verwenden müssen.

Wie du siehst gestaltet sich die Flächenberechnung eines Kreises ganz simpel. Du brauchst lediglich den Radius oder den Durchmesser des Kreises zu kennen.

🔎 Neben der Flächenberechnung eines Kreises ist es oft wichtig, seinen Umfang zu bestimmen. Du kannst mehr über ihn und seine Beziehung zur Fläche in unserem Kreisformeln Rechner erfahren.

Jetzt, wo du weißt, wie der Flächeninhalt eines Kreises berechnet wird, ist vielleicht dein Interesse daran geweckt, auch ähnliche Themen zu entdecken, wie:

den Kreisumfang,
Kreisdiagramme,
die Fläche des Inkreises eines Quadrats, d. h. des größten Kreises, der in das Quadrat passt oder
den Sektor eines Kreises — das ist ein Abschnitt eines Kreises zwischen zwei Radien. Du kannst ihn dir wie ein riesiges Stück Pizza vorstellen.

Sektor eines Kreises und die Formel zur Berechnung der Sektorfläche.

Teste auch unsere anderen Kreisrechner aus:

Flächeninhalt eines Kreissegments Rechner 🇺🇸:

Das ist ein „abgeschnittener“ Teil eines Kreises, der durch eine Kreissehne oder eine Sekante begrenzt wird.

Mittelpunktwinkel Rechner:

Das sind Winkel mit dem Scheitelpunkt in der Mitte des Kreises, deren Schenkel sich bis zum Kreisumfang erstrecken.
Halbkreisfläche Rechner.

Wie wird unser Kreisfläche Rechner verwendet? Durchmesser zu Fläche und Radius zu Fläche.

Spezielle Linien des Kreises – Durchmesser, Radius, Kreissehne und Kreisumfang.

Mit unserem Kreisfläche Rechner kannst du im Handumdrehen die Fläche eines Kreises, seinen Durchmesser und seinen Radius berechnen:

Bestimme, ob dein angegebener Wert der Durchmesser oder der Radius ist, indem du das Bild rechts und die Definitionen aus dem vorherigen Abschnitt verwendest (du kannst den Flächeninhalt eines Kreises sowohl mit dem Durchmesser als auch mit dem Radius berechnen).
Gib den Wert in das entsprechende Feld des Tools ein.
Der Kreisfläche Rechner zeigt dir den Flächeninhalt sofort an! Die Schritt-für-Schritt-Lösung und der genaue Rechenweg erscheinen automatisch direkt unter dem Tool.

So gelingt dir die Flächenberechnun eines Kreises im Handumdrehen 😉.

🔎 Neben dem Maß Flächeninhalt hängt auch der Umfang mit dem Durchmesser zusammen. Erfahre mehr darüber in unserem Umfang zu Durchmesser Rechner.

Wozu berechnen wir den Flächeninhalt eines Kreises?

Der Flächeninhalt des Kreises, der mit dem Radius oder Durchmesser ermittelt wird, dient als Grundlage für viele andere Gleichungen — nicht nur in der Mathematik, sondern auch im täglichen Leben! Hier sind ein paar Beispiele, bei denen das Wissen, wie der Flächeninhalt eines Kreises bestimmt wird, nützlich sein kann:

Wir müssen den Flächeninhalt eines Kreises kennen, um das Volumen eines Kegels zu berechnen 🎉.
Deine Pizza-Party wäre nicht komplett, wenn du nicht die Größe der Pizza mit dem Durchmesser-zu-Fläche-Rechner berechnen könntest 🍕.
Ähnliche Berechnungen verwenden wir, wenn wir die Maße einer Kugel brauchen, z. B. das Kugelvolumen 🌐.
Hast du Lust auf schöne Kleider? Vielleicht liebst du es zu nähen? Effizientes Nähen von Tellerröcken war noch nie so einfach 👗.

FAQs

Wie kann ich den Durchmesser aus der Kreisfläche berechnen?

Mit diesen Formeln lässt sich der Durchmesser aus der Kreisfläche berechnen: Fläche = π ∙ (d/2)² und d = 2 ∙ √(Fläche / π). Zum Beispiel ist der Durchmesser eines Einheitskreises gleich 1,128, da d = 2 ∙ √(1 / π) ≈ 1,128.

Wie groß ist der Radius eines Kreises mit Flächeninhalt 10?

Der Radius beträgt 1,784. Die genaue Antwort lautet √(10 / π). Um dieses Ergebnis zu erhalten, erinnere dich an die Formel Fläche = π ∙ r². Wir wandeln sie in die Form r² = Fläche / π um und sehen, dass der Radius gleich der Quadratwurzel von Fläche / π ist. Wenn wir Fläche = 10 einsetzen, erhalten wir:

Radius = √(10 / π) ≈ √(10 / 3,14) ≈ √3,185 ≈ 1,785.

Wie finde ich den Umfang eines Kreises bei gegebener Fläche?

Um den Umfang eines Kreises aus seiner Fläche zu bestimmen, gehe folgendermaßen vor:

Multipliziere den Flächeninhalt mit π.
Ziehe die Quadratwurzel aus dem Ergebnis von Schritt 1.
Multipliziere mit 2.
Du hast den Umfang des Kreises aus seinem Flächeninhalt ermittelt! Gut gemacht!

Können die Fläche und der Umfang eines Kreises gleich sein?

Ja, die Fläche und der Umfang eines Kreises haben den gleichen Wert 4π, wenn der Radius des Kreises die Länge 2 hat. Bedenke aber, dass die Einheiten unterschiedlich sind! Der Umfang wird in Längeneinheiten, und der Flächeninhalt, nun ja, in Flächeneinheiten ausgedrückt.

Können die Fläche und der Radius eines Kreises gleich sein?

Ja, nimm einen Kreis mit Radius r = 1/π. Dann ist sein Flächeninhalt gleich πr² = π(1/π)² = 1/π, er hat also denselben Wert wie der Radius. Beachte jedoch, dass sich die Einheiten unterscheiden! Der Radius und der Flächeninhalt werden in Einheiten für die Länge bzw. Fläche ausgedrückt; zum Beispiel in cm und in cm².