Mittelpunktswinkel Rechner

Hast du dich jemals gefragt, wie man den Mittelpunktswinkel eines Kreises berechnet? Der Mittelpunktswinkel-Rechner hilft dir dabei. Die einzigen Variablen, die du brauchst, sind die Bogenlänge und der Radius.

Lies weiter, um zu erfahren, was ein Mittelpunktswinkel ist und wie du die Mittelpunktswinkelformel verwendest.

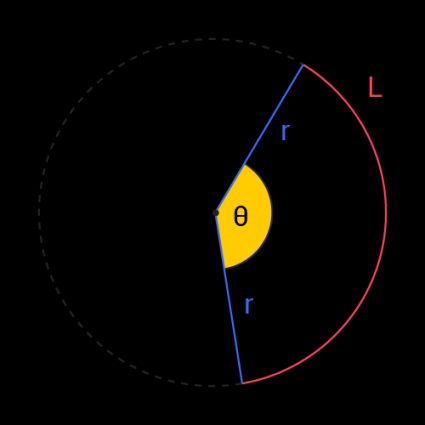
Ein Mittelpunktswinkel ist ein Winkel mit einem Scheitel in der Mitte eines Kreises, dessen Schenkel sich bis zum Kreisumfang erstrecken. Du kannst dir vorstellen, dass der Mittelpunktswinkel an der Spitze einer Pizzascheibe auf einer großen kreisförmigen Pizza liegt.

Du kannst den Mittelpunktswinkel eines Kreises mit der folgenden Formel bestimmen:

θ = b / r

dabei ist θ der Mittelpunktswinkel in Bogenmaß, b die Bogenlänge und r der Radius.

Die Einfachheit der Formel für den Mittelpunktswinkel ergibt sich aus der Definition des Bogenmaßes. Ein Radiant ist eine Einheit der Winkelgröße, wobei 1 Radiant als ein Mittelpunktswinkel (θ) definiert ist, dessen Bogenlänge gleich dem Radius (b = r) ist.

Weil Mathe hungrig macht, können wir den Mittelpunktswinkel vielleicht besser mit Hilfe von Pizza verstehen. Pizzen eignen sich hervorragend, um die Mathematik eines Kreises zu erklären, wie du in unserem Pizzagrößen-Rechner sehen kannst. Wie groß wäre der Mittelpunktswinkel eines Pizzastücks, wenn die Länge der Kruste ($b$) gleich dem Radius ($r$) wäre?

Da die Aufgabe $b = r$ definiert und wir wissen, dass $1$ Radiant als der Mittelpunktswinkel definiert ist. Wenn $b = r$, können wir sehen, dass der Mittelpunktswinkel $1$ Radiant ist. Wir könnten auch die Formel für den Mittelpunktswinkel wie folgt verwenden:

Bei einer komplett kreisförmigen Pizza wissen wir, dass sich die Mittelpunktswinkel aller Scheiben zu 2π Radiant = 360° summieren. Da jede Scheibe einen Mittelpunktswinkel von $1$ Radiant hat, brauchen wir $2\pi / 1 = 2\pi$ Scheiben oder $6,\!28$ Scheiben, um einen kompletten Kreis zu füllen.

Wir kommen auf die gleiche Antwort, wenn wir uns das Problem in Bezug auf die Pizzakruste vorstellen: Der Umfang eines Kreises ist $2\pi r$. Da die Länge der Kruste = der Radius ist, passt die $2\pi r / r = 2\pi$ Kruste auf den Umfang der Pizza.

Wenn du jetzt immer noch hungrig bist, wirf einen Blick auf den Sektorflächenrechner, um den Flächeninhalt jeder Pizzascheibe zu berechnen!

Versuche, den Mittelpunktswinkel-Rechner in umgekehrter Reihenfolge zu benutzen, um diese Aufgabe zu lösen. Die Erde ist etwa 149,6 Millionen km von der Sonne entfernt. Wenn die Erde in jeder Jahreszeit etwa ein Viertel ihrer Bahn zurücklegt, wie viele km legt die Erde dann in jeder Jahreszeit zurück (z. B. vom Frühling zum Sommer)?

Gehen wir dieses Problem Schritt für Schritt an:

1. Vereinfache das Problem, indem du annimmst, dass die Erdumlaufbahn kreisförmig ist (Die Erdumlaufbahn ist in Wirklichkeit elliptisch und ändert sich ständig). In diesem Modell befindet sich die Sonne im Zentrum des Kreises und die Erdumlaufbahn ist der Umfang.

2. Der Radius ist die Entfernung zwischen der Erde und der Sonne: $149,\!6$ Millionen km.

3. Der Mittelpunktswinkel ist ein Viertel des Kreises: $360\degree / 4 = 90\degree$.

4. Benutze den Mittelpunktswinkel-Rechner, um die Bogenlänge zu ermitteln.

Du kannst die endgültige Berechnung selbst ausprobieren, indem du die Formel wie folgt umstellst:

Wandle dann den Mittelpunktswinkel in Bogenmaß um $90\degree = 1,\!57\ \mathrm{rad}$ (benutze unseren Winkelumrechner 🇺🇸, wenn du nicht mehr weißt, wie das geht) und löse die Gleichung:

Wenn wir davon ausgehen, dass die Erde bei einer perfekt kreisförmigen Umlaufbahn pro Saison etwa 234,9 Millionen km zurücklegt!