Kreissektor Fläche Rechner

Mit diesem Kreissektor-Rechner kannst du schnell eine beliebige Kreissektorfläche ermitteln, z. B. die Fläche eines Halbkreises oder eines Quadranten. In diesem kurzen Artikel erfährst du:

• Was ein Kreissektor ist und wie der Kreissektor definiert ist.

• Wir zeigen dir die Formel zur Berechnung der Sektorfläche und, wie du die Gleichung ohne großen Aufwand selbst herleiten kannst.

• Wir zeigen dir auch einige Alltagsbeispiele, für die der Kreissektor-Rechner nützlich sein kann.

Beginnen wir mit der Definition eines Sektors – was ist ein Sektor in der Geometrie?

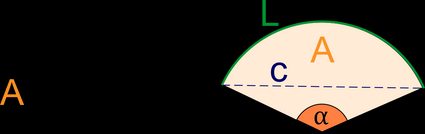
Ein Sektor ist eine geometrische Figur, die von zwei Kreisradien und dem eingeschlossenen Kreisbogen eines Kreises begrenzt wird.

Sektoren eines Kreises werden am häufigsten in Kreisdiagrammen dargestellt, in denen ein Kreis in mehrere Sektoren unterteilt wird. So kann die Gewichtung der einzelnen Segmente am besten dargestellt werden. Die folgenden Bilder zeigen einige Beispiele für Kreissektoren – das bedeutet nicht unbedingt, dass sie wie ein Tortenstück aussehen, sondern eher wie der Rest der Torte, nachdem du dir ein Stück genommen hast:

Über den Sektor einer Ellipse ist eher selten die Rede, die Formeln dazu sind auch viel, viel komplexer als die Gleichungen für den Kreissektor.

Die Formel für den Kreissektor ist einfach: Multipliziere den Mittelpunktswinkel mit dem Radius zum Quadrat und teile das Ergebnis durch 2:

• Kreissektor = r² ∙ α / 2

Aber woraus leitet sich diese Formel ab? Du kannst sie mithilfe von Proportionen ermitteln. Alles, was du dir merken musst, ist die Formel für die Kreisfläche:

1. Die Fläche eines Kreises wird mithilfe der Formel A = πr² berechnet. Das ist ein guter Ausgangspunkt.

2. Der volle Winkel ist 2π im Bogenmaß oder 360° in Grad, wobei letzteres die gängigere Winkeleinheit ist.

3. Jetzt können wir die Fläche eines Teils des Kreises berechnen, welcher durch den Mittelpunktswinkel ausgedrückt wird.

   • Bei einem Winkel von 2π (Vollkreis) ist die Fläche gleich πr²:

     2π → πr².

   • Wie groß ist dann der Flächeninhalt eines Kreissektors?

     α → Kreissektor.

4. Aus der Proportion können wir leicht die endgültige Formel für den Kreissektor finden:

   Kreissektor = α ∙ πr² / 2π = α ∙ r² / 2.

Auf die gleiche Weise kannst du auch die Bogenlänge bestimmen – du musst dir nur die Formel für den Umfang eines Kreises merken. Mehr dazu erfährst du in unserem Kreisumfang Rechner und Bogenlänge Rechner.

Die Fläche eines Halbkreises oder eines Quadranten (Viertelkreis) zu bestimmen, sollte jetzt ein Kinderspiel sein. Überlege einfach, wie viele Teile eines Kreises sie darstellen!

1. Halbkreisfläche: πr² / 2

• Da du weißt, dass das der Hälfte des Kreises entspricht, teile die Fläche durch 2:

  Halbkreisfläche = Kreisfläche / 2 = πr² / 2

• Das gleiche Ergebnis erhältst du natürlich auch, wenn du die Formel für den Flächeninhalt eines Sektors verwendest. Denke nur daran, dass der gerade Winkel π (180°) ist:

  Halbkreisfläche = α ∙ r² / 2 = πr² / 2.

2. Quadrantenfläche: πr² / 4

• Da ein Quadrant ein Viertel eines Kreises ist, können wir die Formel so umschreiben:

  Quadrantenfläche = Kreisfläche / 4 = πr² / 4.

• Der Mittelpunktswinkel des Quadranten ist ein rechter Winkel (π/2 oder 90°), also kommst du schnell auf dieselbe Gleichung:

  Quadrantenfläche = α ∙ r² / 2 = πr² / 4.

Ja, ja, wir wissen schon, was dir durch den Kopf geht: „wozu muss ich das wissen? Ich werde das sowieso niemals brauchen“. Nun, Geometrie ist überall um uns herum:

• Wenn du dich fragst, wie groß die Torte sein muss, die du für deine Geburtstagsparty bestellen möchtest — Bingo, nutze die Formel für den Kreissektor, um die Größe eines Stücks 🍰 für deine Gäste abzuschätzen, damit niemand vernachlässigt wird.

• Die Sache mit Pizza ist ganz ähnlich — ist dir aufgefallen, dass jedes Stück ein Kreissektor ist 🍕? Wenn du zum Beispiel kein großer Fan der Kruste bist, kannst du ausrechnen, welche Pizzagröße der beste Deal für dich ist.

• Gibt es hier Nähbegeisterte?👗 Die Berechnung der Kreisfläche kann bei der Vorbereitung eines kreisförmigen Rocks nützlich sein (da es sich nicht immer um einen Vollkreis handelt, sondern um einen Kreissektor).

Abgesehen von diesen Alltagsbeispielen kann die Formel für den Kreissektor auch in der Geometrie nützlich sein, z. B. um den Flächeninhalt eines Kegels zu bestimmen.