Verhältnis Rechner

Der Verhältnisrechner hilft dir, identische Verhältnisse zu berechnen, wenn drei der vier Teile der beiden Verhältnisse gegeben sind. Ein Verhältnis ist eine Beziehung zwischen zwei Mengen, die oft als Bruch dargestellt wird. Es zeigt an, wie viel von einem Teil in einem anderen Teil enthalten ist und stellt im Grunde einen Bruchteil oder einen prozentualen Anteil des Ganzen dar.

Bevor wir den Rechner benutzen können, müssen wir verstehen, wie man Verhältnisse aufstellt und wie man ein Verhältnis findet.

Ein Verhältnis besteht aus zwei Teilen, genauso wie ein Bruch aus zwei Teilen besteht. Es gibt den Zähler (die obere Zahl des Bruchs) und den Nenner (die untere Zahl des Bruchs).

Nehmen wir zum Beispiel an, es gibt einen Kuchen, der in acht Stücke geschnitten ist und drei der acht Stücke wurden gegessen. Wenn wir das Verhältnis zwischen den gegessenen Stücken und der gesamten Torte wissen möchten, müssen wir die Anzahl der gegessenen Stücke in den Zähler und die Gesamtzahl aller Stücke in den Nenner schreiben: 3/8.

Das ist das einfachste aller Verhältnisse, da es keine Vereinfachung erfordert. Aber was ist, wenn wir das Verhältnis vereinfachen oder ein größeres, aber gleichwertiges Verhältnis erhalten wollen? Im nächsten Abschnitt über die Ermittlung eines Verhältnisses wird das Verfahren erklärt.

Angenommen, wir haben dasselbe Verhältnis von 3/8, möchten es aber auf ein größeres, gleichwertiges Verhältnis mit einem Nenner von 72 erweitern. Dazu müssen wir ein Proportionsverhältnis aufstellen, d.h. zwei Verhältnisse, die gleich groß sind, und nach dem fehlenden Teil auflösen. Wir können dies wie folgt tun:

1. Schreibe beide Verhältnisse als Brüche auf und kennzeichne den fehlenden Teil mit einem x.
2. Setze die Brüche gleich, um ein Verhältnis zu bilden.
3. Nutze das Verfahren der Kreuzmultiplikation, um die Variable zu isolieren.
4. Löse nach x auf.
5. Verwende den Verhältnisrechner, um deine Antwort zu überprüfen.

Im obigen Beispiel würden die Schritte wie folgt aussehen:

1. 3/8 = x/72;
2. 8 - x = 72 - 3;
3. 8x = 216;
4. x = 27.

Für komplexere Verhältnisse, die größere Zahlen oder Dezimalzahlen beinhalten, ist der Verhältnisrechner viel praktischer. Der Verhältnisrechner 🇺🇸, der das Gleiche tut, kann auch verwendet werden, um Probleme wie das obige zu lösen.

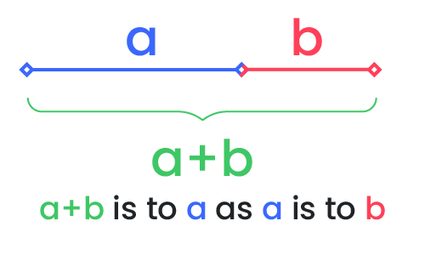
Der Goldene Schnitt ist ein spezielles Verhältnis, das erreicht wird, wenn zwei Mengen das gleiche Verhältnis haben wie das Verhältnis ihrer Summe zu der größeren der beiden Mengen. Wenn wir die beiden Mengen mit a und b bezeichnen, dann lautet der Goldene Schnitt (a+b)/a = a/b. Der Wert dieses Quotienten ist ungefähr 1,618. Berechne dies mit dem goldenen Schnitt-Rechner.

Man sagt, dass das Goldene Rechteck das ästhetischste Rechteck für das Auge ist. Das ist ein Rechteck mit der Länge a + b und der Breite a. Das Rechteck ist golden, wenn (a+b)/a = a/b gilt. Der Goldenes-Rechteck-Rechner berechnet die Länge und Breite, die nötig sind, um das perfekte Goldene Rechteck zu erhalten.

Der Verhältnisrechner ist auch bei der geometrischen Anwendung von ähnlichen Dreiecken hilfreich. Wenn die Seiten eines Dreiecks im Verhältnis zu den Seiten eines anderen Dreiecks stehen, werden die beiden Dreiecke als ähnlich bezeichnet. Das gilt auch für andere Polygone.