Goldener Schnitt Rechner
Der Goldener-Schnitt-Rechner berechnet die Länge der Teilstrecken, die dazu nötig sind, den Goldenen Schnitt zu erhalten. Bevor wir zur Berechnung des Goldenen Schnitts übergehen, wollen wir dir erst einmal erklären, was es mit dem Goldenen Schnitt überhaupt auf sich hat. In den nächsten Zeilen findest du alles, was du darüber wissen musst!
Du kannst dir auch den Proportionsrechner 🇺🇸 ansehen, wenn du etwas über Verhältnisse im Allgemeinen lernen willst.
Definition des Goldenen Schnitts
Der Goldene Schnitt entsteht durch die Unterteilung einer Strecke in zwei Teilstrecken – das Verhältnis des längeren zum kürzeren Streckenteils muss dabei gleich dem Verhältnis der Gesamtstrecke zum längeren Teil sein. Das heißt also, dass, wenn der längere Teil die Länge und der kürzere Teil die Länge hat, die Formel für den Goldenen Schnitt folgendermaßen lautet:
Um das Teilungsverhältnis des Goldenen Schnitts zu berechnen, musst du die obige Gleichung für lösen. Zu diesem Zweck können wir die Formel folgendermaßen umstellen:
Am Ende müssen wir also nur noch die quadratische Gleichung für lösen. Dies tätigen wir mit den üblichen Methoden und können dabei feststellen, dass das Teilungsverhältnis für den Goldenen Schnitt gleich ist, was ungefähr der Zahl entspricht. Diese Zahl wird oft mit dem griechischen Buchstaben bezeichnet.
🙋 Der Goldene Schnitt stimmt mit dem Grenzwert des Verhältnisses der aufeinanderfolgenden Fibonacci-Zahlen überein! Ist das etwa Magie? Mit unserem Fibonacci-Folge Rechner kannst du mehr darüber erfahren!
Wir wissen jetzt, was der Goldene Schnitt ist und wie man das entsprechende Teilungsverhältnis berechnet. Jetzt wollen wir herausfinden, ob zwei gegebene Längen dieses göttliche Verhältnis erfüllen.
Wie prüfe ich, ob zwei Strecken im Goldenen-Schnitt-Verhältnis zueinander stehen?
Hier findest du eine Schritt-für-Schritt-Anleitung, mit der du herausfinden kannst, ob zwei Strecken im Goldenen-Schnitt-Verhältnis zueinander stehen:
- Finde die Länge der längeren Strecke und benenne sie
a. - Bestimme die Länge der kürzeren Strecke und benenne sie
b. - Berechne
a/b. - Wenn das Verhältnis (ungefähr) gleich
1,618ist, folgen die Strecken dem Prinzip des Goldenen Schnitts.
Zu diesem Zweck kannst auch einfach Omni's Goldener-Schnitt-Rechner verwenden. Obwohl dir bei dieser Berechnung jeder Quotientenrechner helfen kann, ist unser Goldener-Schnitt-Rechner jedoch genau auf dieses Thema spezialisiert und ist somit die beste Wahl!
Wie benutzt man diesen Goldener-Schnitt-Rechner?
Der Goldener-Schnitt-Rechner von Omni könnte nicht benutzerfreundlicher und unkomplizierter sein. Er hat drei Felder, die den drei Längen ,die in der Formel für den Goldenen Schnitt vorkommen, entsprechen. Und du musst nur eine davon eingeben, damit die beiden anderen automatisch berechnet werden. Ist das nicht großartig?
Goldenes Rechteck
Das Goldene Rechteck ist ein Rechteck, dessen Seitenlängen im perfekten Verhältnis (dem Goldenen Schnitt entsprechend) zueinander stehen, d. h. das Verhältnis der Länge zur Breite beträgt . Dieses Rechteck wird oft in der Kunst angewandt, da es als das fürs menschliche Auge am angenehmsten anzuschauende Rechteck gilt. Mit dem Goldenes Rechteck Rechner kannst du die Seiten eines Goldenen Rechtecks ganz bequem bestimmen, ohne sie von Hand ausrechnen zu müssen.
Warum ist der Goldene Schnitt wichtig?
Der Goldene Schnitt hat dank seiner Eigenschaften und Erscheinung schon immer eine besondere Bedeutung in der Wissenschaft und Kunst gehabt. Apropos Mathe:
- Ein Goldenes Rechteck kann in zwei kleinere goldene Rechtecke geteilt werden (wobei es seine Proportionen beibehält).
- Der Goldene Schnitt ist eng mit der Zahl
5verknüpft. Diese Zahl taucht in der Definition des Goldenen Schnitts (φ = (1 + √5)/2) auf; in einem Fünfeck entspricht das Verhältnis zwischen einer Diagonale und einer Seite dem Teilungsverhältnis des Goldenen Schnitts.
In der Kunst taucht der Goldene Schnitt erst später auf: Dalí zum Beispiel hat dieses Verhältnis in vielen seiner Werke verwendet.
Wo kann man den Goldenen Schnitt in der Natur finden?
Viele historische und zeitgenössische Quellen behaupten, dass der Goldene Schnitt in der Natur allgegenwärtig ist. Einige Beispiele sind:
- das Wachstumsmuster von Blättern,
- die geometrischen Oberflächen einiger Gemüse und Muscheln,
- die Proportionen der Knochen von einigen Tieren.
Obwohl wir das Vorhandensein von geometrischen Mustern in der Natur nicht leugnen können, kann man auch nicht behaupten, dass die Proportionen der oben genannten Beispiele exakt sind: einige weisen große Abweichungen auf, während andere dem Goldenen Schnitt nur nahekommen.
Was ist der Goldene Schnitt?
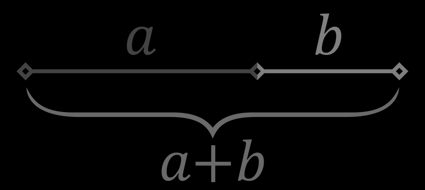
Man spricht von Goldenem Schnitt, wenn das Verhältnis der längeren zu der kürzeren Teilstrecke, gleich dem Verhältnis der Summe ihrer Längen zu der längeren der beiden Strecken ist. Wenn wir dies nun mathematisch beschreiben wollen, dann sind a und b nach Goldenem Schnitt unterteilt, wenn:
a/b = (a + b)/a
Das Teilungsverhältnis des Goldenen Schnittes, welches man bei dieser Division erhält, beträgt ungefähr 1,618.
Wie lang sind die Seiten eines goldenen Rechtecks mit der Diagonalen 1?
Die Seiten eines Goldenen Rechtecks mit der Diagonalen d = 1 sind a = 0,850651 und b = 0,525731. Um diese Werte zu finden:
-
Wende den Satz des Pythagoras an, um die Länge der Seite
bin Abhängigkeit vonazu bestimmen:b = √(1 - a²). -
Berechne die Länge der Seite
aunter der Annahme, dassa/b = φist:a/b = φ
a/√(1 - a²) = φ
a = √(φ²/(1 + φ²)) = 0,850651 -
Berechne die Länge der Seite
bmit der folgenden Formel:b = a/φ = 0,525731
Fertig!