Wahrscheinlichkeitsrechner
Mit dem Wahrscheinlichkeitsrechner kannst du die Wahrscheinlichkeit der Zusammenhänge zwischen zwei verschiedenen Ereignissen untersuchen. Wenn z. B. die Wahrscheinlichkeit, dass A oder B eintritt, jeweils 50 % beträgt, wie hoch ist dann die Wahrscheinlichkeit, dass beide Ereignisse eintreten? Oder dass nur eines eintritt, dass mindestens eines eintritt, dass keines der beiden eintritt usw.?
Unser Wahrscheinlichkeitsrechner liefert dir grundsätzlich sechs Optionen. Wenn du angibst, „wir oft die Würfel gefallen sind”, bietet dir der Rechner zusätzlich sechs weitere Optionen. Mit dem Wissen, wie die Wahrscheinlichkeit einzelner Ereignisse ermittelt wird, kannst du viel Zeit sparen.
Mit unserem Rechner kannst du:
- herausfinden, wie du den Wahrscheinlichkeitsrechner richtig verwendest,
- von Einzelereignissen die Wahrscheinlichkeit berechnen,
- Stochastik Grundlagen und Stochastik Formeln kennenlernen,
- mehrere Beispiele für die Wahrscheinlichkeitrechnung sowie für bedingte Wahrscheinlichkeiten sehen,
- den Unterschied zwischen theoretischer und empirischer Wahrscheinlichkeit verstehen,
- stochastische Abhängigkeit und stochastische Unabhängigkeit verstehen, und
- dein Wissen über die Beziehung zwischen Wahrscheinlichkeit und Statistik vertiefen.
Du bist eigentlich hierhergekommen, um deine Chancen auf den Gewinn einer Wette oder den Jackpot zu überprüfen? Unser Chancenrechner und Lotterie Rechner 🇺🇸 helfen dir dabei!
Stochastik Grundlagen: Wahrscheinlichkeit berechnen und Wahrscheinlichkeitsdefinition
Die grundlegende Definition der Wahrscheinlichkeit ist das Verhältnis aller günstigen Ergebnisse zur Anzahl aller möglichen Ergebnisse.
Die Werte einer einzelnen Wahrscheinlichkeit befinden sich zwischen 0 und 1, daher werden Wahrscheinlichkeiten in der Regel auch als Prozentsätze angegeben. Die Wahrscheinlichkeit eines einzelnen Ereignisses kann wie folgt ausgedrückt werden:
- die Wahrscheinlichkeit von
A:P(A), - die Wahrscheinlichkeit von
B:P(B), - die Wahrscheinlichkeit von
+:P(+), - die Wahrscheinlichkeit von
♥:P(♥)usw.
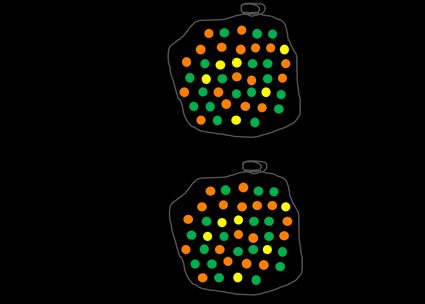
Schauen wir uns ein Beispiel mit mehrfarbigen Bällen an. Wir haben einen Beutel, der mit orangefarbenen, grünen und gelben Bällen gefüllt ist. Unser Ereignis "A" besteht darin, einen zufälligen Ball aus dem Beutel zu nehmen. Wir können Ω (Ohm) als die Gesamtmenge der Bälle definieren. Die Wahrscheinlichkeit des Ereignisses Ω, d.h. des Auswählens eines beliebigen Balls, ist natürlich 1. Tatsächlich ist die Summe aller möglichen Ereignisse in einer gegebenen Menge immer gleich 1.
Betrachten wir nun etwas Anspruchsvolleres – wie groß ist die Wahrscheinlichkeit, einen orangefarbenen Ball zu ziehen? Um diese Frage zu beantworten, müssen wir die Anzahl aller orangefarbenen Bälle ermitteln und durch die Anzahl aller Bälle im Beutel dividieren. Du kannst dies für jede beliebige Farbe tun, z. B. gelb. Du wirst feststellen, dass die Wahrscheinlichkeit, einen Ball aus dem Beutel zu ziehen, umso höher ist, je mehr Bälle dieser Farbe vorhanden sind, wenn der Vorgang völlig zufällig ist.
Schaue dir unseren Wahrscheinlichkeitsrechner für 3 Ereignisse und den Bedingte Wahrscheinlichkeit Rechner 🇺🇸 an, um die Chancen mehrerer Ereignisse zu bestimmen.

Ein komplementäres Ereignis, welches als nicht A definiert ist, wird als Ā oder A' ausgedrückt.
In unserem Beispiel wird die Wahrscheinlichkeit, KEINEN orangefarbenen Ball auszuwählen, als Anzahl aller nicht-orangenen Bälle geteilt durch die Summe aller Bälle beschrieben. Die Summe P(A) + P(Ā) ist immer 1, da es keine Möglichkeiten wie einen halben Ball oder einen halb-orangen Ball gibt.
Versuche nun, die Wahrscheinlichkeit zu ermitteln, einen blauen Ball zu ziehen. Du wirst scheitern, egal wie sehr du dich bemühst. Die Wahrscheinlichkeit ist gleich 0, da sich kein blauer Ball im Beutel befindet.
Wir verwenden ständig intuitive Wahrscheinlichkeitsrechnungen. Für statistische Analysen ist es wichtig, zu wissen, wie die Wahrscheinlichkeit quantifiziert wird. Das ermöglicht es dir, dieses ansonsten nebulöse Konzept namens "Wahrscheinlichkeit" zu messen. Darüber hinaus ist die relative Häufigkeit bei einem diskreten Datensatz für jeden Wert gleichbedeutend mit der Wahrscheinlichkeit seines Auftretens.
Du suchst etwas anderes? Wirf einen Blick auf unseren Nachtest Wahrscheinlichkeitsrechner 🇺🇸. 🎲
Wie verwendest du unseren Wahrscheinlichkeitsrechner?
Um unseren Rechner optimal nutzen zu können, führe die folgenden Schritte durch:
1. Definiere das Problem, das du lösen möchtest.
Dein Problem muss in zwei unabhängige Ereignisse zusammengefasst werden.
2. Bestimme die Wahrscheinlichkeit jedes Ereignisses.
Wenn du nun weißt, wie du die Wahrscheinlichkeit eines einzelnen Ereignisses berechnen kannst, musst du nur noch alle erforderlichen Werte ermitteln.
3. Gib die prozentuale Wahrscheinlichkeit für jedes Ereignis in die entsprechenden Felder des Rechners ein.
Der Wahrscheinlichkeitsrechner zeigt dir sofort die genauen Wahrscheinlichkeiten für 6 verschiedene Szenarien an:
- beide Ereignisse werden eintreten,
- mindestens eines der Ereignisse wird eintreten,
- genau eines der Ereignisse wird eintreten,
- keines der Ereignisse wird eintreten,
- nur das erste Ereignis wird nicht eintreten oder
- nur das zweite Ereignis wird nicht eintreten.
Der Rechner zeigt auch die Wahrscheinlichkeit von sechs weiteren Szenarien an, wenn eine bestimmte Anzahl von Versuchen gegeben ist:
- A tritt immer ein,
- A tritt nie ein,
- A tritt mindestens einmal ein,
- B tritt immer ein,
- B tritt nie ein oder
- B tritt mindestens einmal ein.
Du kannst die Anzahl der Versuche und jedes andere Feld des Rechners ändern – die anderen Felder passen sich automatisch an. Diese Funktion spart dir eine Menge Zeit, wenn du z. B. herausfinden möchten, wie hoch die Wahrscheinlichkeit von Ereignis B sein müsste, damit die Wahrscheinlichkeit, dass beide Ereignisse eintreten, 50 % beträgt.
Wenn die Menge der Wahlmöglichkeiten extrem groß ist und nur wenige Ergebnisse positiv sind, ist die resultierende Wahrscheinlichkeit winzig, etwa P(A) = 0,0001. Es ist praktisch, die wissenschaftliche Notation zu verwenden (0,0001 = 10-4), um die Anzahl der Nullen nicht zu verwechseln.
Bedingte Wahrscheinlichkeit
Eine der wichtigsten Überlegungen in der Welt der Wahrscheinlichkeiten ist, ob eine stochastische Abhängigkeit vorliegt, oder nicht, also ob die Ereignisse voneinander abhängig sind. Zwei Ereignisse sind unabhängig, wenn das Eintreten des ersten Ereignisses keinen Einfluss auf die Wahrscheinlichkeit des Eintretens des zweiten Ereignisses hat. Ist das erfüllt, haben wir eine stochastische Unabhängigkeit. Wenn wir zum Beispiel einen perfekt ausbalancierten kubischen Standardwürfel werfen, ist die Wahrscheinlichkeit, eine Zwei ⚁ zu erhalten, gleich 1/6 (genauso wie die Wahrscheinlichkeit, eine Vier ⚃ oder eine andere Zahl zu erhalten). Die Ereignisse sind unabhängig voneinander.
Nehmen wir an, du würfelst zweimal und erhältst im ersten Wurf die Augenzahl Fünf ⚄. Wenn du dich fragst, wie hoch die Wahrscheinlichkeit ist, dass du im zweiten Wurf eine Zwei ⚁ würfelst, lautet die Antwort, aufgrund der Unabhängigkeit der Ereignisse, 1/6.
Die Berechnung sieht anders aus, wenn eines der Ereignisse das ganze System beeinflusst. Hierbei handelt es sich um die bedingte Wahrscheinlichkeit.
Nehmen wir an, wir haben 10 verschieden nummerierte Billardkugeln, von ➀ bis ➉. Du wählst eine zufällige Kugel, sodass die Wahrscheinlichkeit, die ➆ zu bekommen, genau 1/10 ist. Nehmen wir an, du entfernst die Drei ➂ aus dem Spiel. Dann fragst du dich noch einmal, wie hoch die Wahrscheinlichkeit ist, die Sieben ➆ zu bekommen. Die Situation hat sich geändert – die Kugel ➆ ist jetzt eine von neun Kugeln, was bedeutet, dass die Wahrscheinlichkeit sie zu wählen 1/9 beträgt. Die Frage kann auch so gestellt werden: „Wie hoch ist die Wahrscheinlichkeit, eine ➆ zu wählen, WENN die erste Kugel eine ➂ war?“
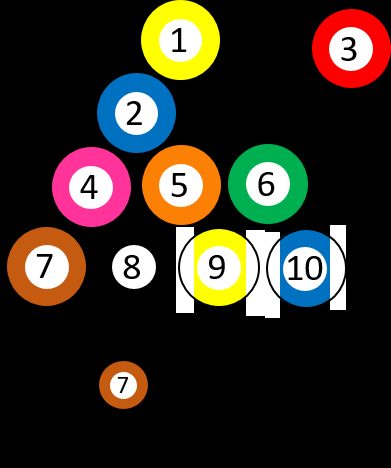
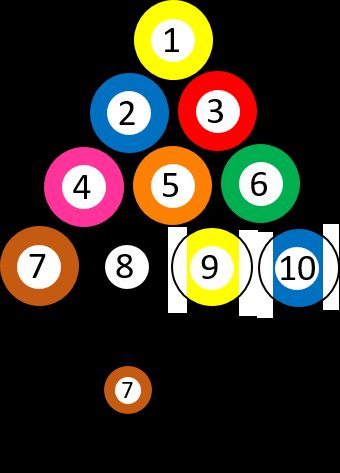
Nehmen wir ein anderes Beispiel: Stell dir vor, du wirst eine Prüfung in Statistik schreiben. Von deinen Kommilitonen aus höheren Semestern weißt du, dass die Prüfung anspruchsvoll ist und die Wahrscheinlichkeit, dass du sie im ersten Semester bestehen wirst, bei 0,5 liegt (letztes Jahr haben 18 von 36 Studenten bestanden). Dann stellst du dir die Frage: „Wie hoch ist meine Wahrscheinlichkeit, die Prüfung zu bestehen, WENN ich mich bereits mit dem Thema beschäftigt habe?“ 20 Personen gaben zu, ihre Notizen mindestens einmal vor der Prüfung durchgelesen zu haben, und 16 von ihnen hatten die Prüfung bestanden. Die Antwort auf unsere Frage ist 16/20 = 0,8 – die Wahrscheinlichkeit, dass du die Prüfung bestehst, wenn du dir deine Notizen vorher angeschaut hast, liegt bei 80 %. Dieses Ergebnis zeigt, dass diese zusätzliche Bedingung relevant ist, wenn wir herausfinden wollen, ob Lernen etwas an deinem Prüfungsergebnis verändert oder nicht.
Wenn du das Konzept der bedingten Wahrscheinlichkeit noch nicht ganz verstanden hast, schaue dir das folgende Beispiel an: Du fährst mit dem Auto von Stadt X nach Stadt Y. Die Entfernung zwischen den beiden Städten beträgt etwa 150 Kilometer. Mit einem vollen Tank schaffst du es, ca. 500 Kilometer weit zu fahren. Wenn du nicht weißt, wie voll dein Auto getankt ist, kannst du die Wahrscheinlichkeit dafür abschätzen, dass du das Ziel ohne zwischendurch zu tanken erreichst. Und was ist, wenn jemand das Auto bereits voll getankt hat? Jetzt kannst du dir fast sicher sein, dass du das Ziel ohne Zwischentanken erreichen wirst (es sei denn, andere Probleme verhindern es).
Bedingte Wahrscheinlichkeit: Stochastik Formeln und Baumdiagramm
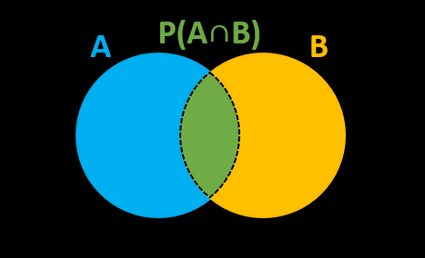
Der formale Ausdruck der bedingten Wahrscheinlichkeit, die als P(A|B), P(A/B) oder PB(A) bezeichnet wird, kann wie folgt berechnet werden:
P(A|B) = P(A∩B) / P(B),
wobei P(B) die Wahrscheinlichkeit eines Ereignisses B und P(A∩B) (sprich: P von A und B) die gemeinsame Wahrscheinlichkeit der beiden Ereignisse ist. Andererseits können wir die Schnittmenge zweier Ereignisse schätzen, wenn wir eine der bedingten Wahrscheinlichkeiten kennen:
P(A∩B) = P(A|B) ∙ P(B)oderP(A∩B) = P(B|A) ∙ P(A).
Es ist einfacher, das Konzept der bedingten Wahrscheinlichkeit anhand eines Baumdiagramms zu verstehen. Wir fragten Schüler in einer Klasse, ob sie Mathe und Physik mögen. Das Ereignis M steht für den Prozentsatz der Schüler, die Mathe mögen, und P für den Prozentsatz der Schüler, die Physik mögen. In der nachfolgenden Abbildung, siehst du die Darstellung von bedingten Wahrscheinlichkeiten anhand dieses Beispiels in einem Baumdiagramm.

Es gibt einen berühmten Lehrsatz, welcher die bedingten Wahrscheinlichkeiten von zwei Ereignissen miteinander verbindet. Er heißt Satz von Bayes – die Formel lautet wie folgt:
P(A|B) = P(B|A) ∙ P(A) / P(B)
Der Satz von Bayes beantwortet die Frage: „Wie hoch ist die Wahrscheinlichkeit von A wenn B eingetreten ist, wenn ich die Wahrscheinlichkeit von B wenn A eingetreten ist kenne?“. Dieser Lehrsatz liefert manchmal überraschende und unintuitive Ergebnisse. Die am häufigsten verwendeten Beispiele sind Testverfahren für Medikamente und die Erkennung von Krankheiten, die viel mit dem relativen Krankheitsrisiko der Bevölkerung zu tun haben. Bleiben wir bei dem zweiten Beispiel. In einer Gruppe von 1000 Menschen haben 10 von ihnen eine seltene Krankheit. Alle 1000 Menschen haben einen Test gemacht, der in 95% der Fälle das tatsächliche Ergebnis zeigt. Wir wollen nun herausfinden, wie hoch die Wahrscheinlichkeit ist, dass eine Person krank ist, wenn sie positiv getestet wird.
Intuitiv würde man raten, dass das Ergebnis bei etwa 90 % liegen müsste, oder? Lass uns einige Berechnungen anstellen und die richtige Antwort herausfinden.
- Wir verwenden die folgende Notation:
G– gesund,K– krank,+– Test positiv,-– Test negativ. - Schreibe die Informationen aus dem obigen Text in Form von Wahrscheinlichkeiten um:
P(G) = 0,99,P(K) = 0,01,P(+|K) = 0,95,P(-|K) = 0,05,P(+|G) = 0,05,P(-|G) = 0,95. - Berechne die Gesamtwahrscheinlichkeit, dass ein Test positiv ist:
P(+) = P(+|K) ∙ P(K) + P(+|G) ∙ P(G) = 0,95 ∙ 0,01 + 0,05 ∙ 0,99 = 0,059. - Verwende den Satz von Bayes, um die bedingte Wahrscheinlichkeit
P(K|+) = P(+|K) ∙ P(K) / P(+) = 0,95 ∙ 0,01 / 0,059 = 0,161zu finden.
Hmm... so hoch ist diese Wahrscheinlichkeit doch nicht, oder? Es stellt sich heraus, dass diese Art von Paradoxon dann auftritt, wenn ein signifikantes Ungleichgewicht zwischen der Anzahl gesunder und kranker Menschen oder allgemein zwischen zwei verschiedenen Gruppen besteht. Wenn das Ergebnis positiv ist, lohnt es sich immer, den Test zu wiederholen, um eine korrekte Diagnose zu stellen.
Wahrscheinlichkeitsverteilung und kumulative Verteilungsfunktion
Je nachdem, ob es sich um diskrete oder stetige Zufallsvariablen handelt, kann man zwischen zwei Arten von Wahrscheinlichkeitsverteilungen unterscheiden.
-
Eine diskrete Wahrscheinlichkeitsverteilung beschreibt die Wahrscheinlichkeit des Auftretens von abzählbaren, unterschiedlichen Ereignissen. Ein Beispiel ist die Binomialverteilung, die die Wahrscheinlichkeit eines Erfolges bei mehreren Versuchen berücksichtigt, z. B. beim Werfen einer Münze. Im Gegensatz dazu ist bei der negativen Binomialverteilung (auch bekannt als Pascal-Verteilung) die feste Anzahl der Erfolge gegeben, und man möchte die Gesamtzahl der Versuche schätzen.
Die Poisson-Verteilung ist eine weitere diskrete Wahrscheinlichkeitsverteilung und ist eigentlich ein Sonderfall der Binomialverteilung. Du kannst sie mit unserem Poisson Verteilungsrechner 🇺🇸 berechnen. Die Wahrscheinlichkeitsfunktion kann als eine weitere Definition einer diskreten Wahrscheinlichkeitsverteilung interpretiert werden – sie ordnet jedem möglichen Ereignis eine Wahrscheinlichkeit zu. Die geometrische Verteilung ist ein hervorragendes Beispiel für die Verwendung der Wahrscheinlichkeitsfunktion. Du findest mehr zu diesem Thema in unserem geometrische Verteilung Rechner 🇺🇸.
-
Eine stetige Wahrscheinlichkeitsverteilung enthält Informationen über nicht abzählbare Ereignisse. Es ist nicht möglich, die Wahrscheinlichkeit eines einzelnen Ereignisses vorherzusagen (wie es bei der diskreten Verteilung der Fall war). Es wird vielmehr die Wahrscheinlichkeit bestimmt, dass das Ergebnis in einem Bereich zwischen zwei bestimmten Werten liegt. Die Normalverteilung ist eine der bekanntesten stetigen Verteilungsfunktionen. Sie kann zur Modellierung einer Reihe von Eigenschaften innerhalb der Bevölkerung verwendet werden, z. B. der Körpergröße erwachsener Menschen oder der IQ-Verteilung. Die Funktion, die die Wahrscheinlichkeit beschreibt, ein Ergebnis innerhalb eines bestimmten Wertebereich zu erhalten, wird Wahrscheinlichkeitsdichtefunktion genannt.
Wenn du in der Wahrscheinlichkeitstheorie und -berechnung fortgeschrittener bist, solltest du dich auf jeden Fall mit der SMp(x) Verteilung 🇺🇸 beschäftigen, die die Kombination mehrerer diskreter und stetiger Wahrscheinlichkeitsfunktionen berücksichtigt.
Für jede Wahrscheinlichkeitsverteilung können wir die (kumulative) Verteilungsfunktion (CDF – Cumultative Distribution Function) konstruieren. Sie gibt an, wie hoch die Wahrscheinlichkeit ist, dass eine Variable den Wert kleiner oder gleich einer bestimmten Zahl annimmt.
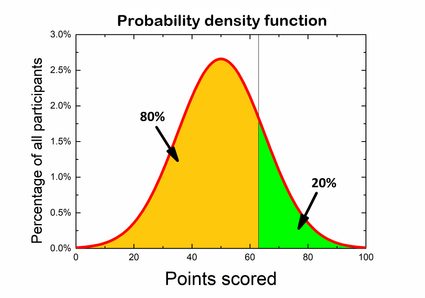
Sagen wir mal, du nimmst an einem Quiz zu Allgemeinwissen teil. Der Wettbewerb besteht aus 100 Fragen und für eine richtige Antwort gibt es 1 Punkt, für eine falsche Antwort gibt es keine Punkte. Aus den Ergebnissen vorheriger Teilnehmer lässt sich eine Wahrscheinlichkeitsverteilung erstellen. Die Regeln besagen, dass nur 20 % der besten Teilnehmer einen Preis erhalten, und du fragst dich, wie gut du abschneiden müsstest, um zu den Gewinnern zu gehören. Du kannst dir ein Diagramm vorstellen, welches du so aufteilst, dass 80% der Fläche unter der Linie auf der linken Seite der gewünschten Punktzahl liegt und 20% der Ergebnisse rechts von der gewünschten Punktzahl liegen. Was du hier eigentlich suchen, ist ein linksseitiger p-Wert.
Es gibt jedoch auch einen anderen Weg, den gewünschten Wert zu finden – wir können eine kumulative Verteilungsfunktion verwenden. Finde einfach den Wert 80% auf der Abszissenachse und die entsprechende Anzahl von Punkten auf der y-Achse, ohne irgendetwas zu berechnen!
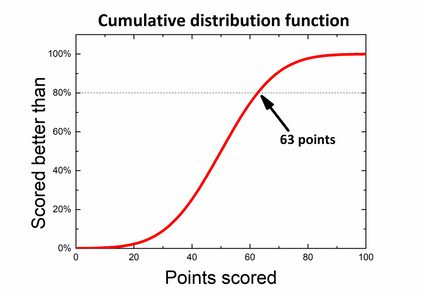
Theoretische vs. experimentelle Wahrscheinlichkeit
Bei fast allen oben beschriebenen Beispielen handelt es sich um die theoretische Wahrscheinlichkeit. Es stellt sich also die Frage: Was ist der Unterschied zwischen theoretischer und experimenteller (auch empirischer) Wahrscheinlichkeit? Die formale Definition der theoretischen Wahrscheinlichkeit ist das Verhältnis zwischen der Anzahl der günstigen Ergebnisse und der Anzahl aller möglichen Ergebnisse. Sie beruht auf den gegebenen Informationen und logischen Überlegungen und sagt uns, was wir von einem Experiment erwarten können.
Betrachten wir noch einmal den Beutel mit den bunten Bällen. Es gibt insgesamt 42 Bälle, und 18 davon sind orange. Das Spiel besteht darin, einen zufälligen Ball aus dem Beutel zu nehmen und ihn vor der nächsten Ziehung wieder hineinzulegen, sodass sich immer 42 Bälle im Beutel befinden. Wenn wir die Wahrscheinlichkeitsdefinition anwenden, können wir die Wahrscheinlichkeit, einen orangefarbenen Ball zu ziehen schnell auf 18/42 schätzen, oder, um den Bruch zu vereinfachen, 3/7. Das bedeutet, dass, wenn wir 14 Bälle auswählen, 6 orangefarbene Bälle darunter sein sollten.
Die experimentelle Wahrscheinlichkeit hingegen sagt uns genau, was passiert ist, wenn wir ein Experiment durchführt haben, und nicht, was passieren sollte. Sie basiert auf dem Verhältnis zwischen der Anzahl der erfolgreichen und der Anzahl aller Versuche. Bleiben wir bei demselben Beispiel – nimm einen zufälligen Ball aus dem Beutel und wiederhole den Vorgang noch 13 Mal. Angenommen, du erhältst 8 orangefarbene Bälle bei 14 Versuchen. Dieses Ergebnis bedeutet, dass die empirische Wahrscheinlichkeit 8/14 oder 4/7 beträgt.
Wie du siehst, weicht dieses Ergebnis von dem theoretischen Ergebnis ab. Das ist nicht weiter verwunderlich, denn wenn du versuchst, dieses Spiel immer und immer wieder zu wiederholen, wirst du manchmal mehr, manchmal weniger und manchmal genau die theoretisch vorhergesagte Zahl erreichen. Wenn du alle Ergebnisse zusammenzählst, solltest du feststellen, dass die Gesamtwahrscheinlichkeit immer näher an die theoretische Wahrscheinlichkeit herankommt. Wenn das nicht der Fall ist, liegt der Verdacht nahe, dass die Auswahl der Bälle aus dem Beutel nicht ganz zufällig ist, z. B. weil die Bälle verschiedener Farben unterschiedlich groß sind, sodass du sie unterscheiden kannst, ohne hinschauen zu müssen.
Wahrscheinlichkeitsrechnung und Statistik
Sowohl die Statistik als auch die Wahrscheinlichkeitsrechnung sind Zweige der Mathematik und befassen sich mit der Beziehung zwischen dem Auftreten von Ereignissen. Jeder sollte sich jedoch der Unterschiede bewusst sein, die sie zu zwei verschiedenen Bereichen machen.
-
Die Wahrscheinlichkeitsrechnung ist im Allgemeinen ein theoretisches Gebiet der Mathematik und untersucht die Folgen mathematischer Definitionen und Sätze. Im Gegensatz dazu ist die Statistik in der Regel eine praktische Anwendung der Mathematik in alltäglichen Situationen und versucht, den Beobachtungen in der realen Welt einen Sinn zu geben und sie zu verstehen.
-
Die Wahrscheinlichkeitsrechnung sagt die Möglichkeit des Eintretens von Ereignissen voraus, während die Statistik im Wesentlichen die Häufigkeit des Auftretens vergangener Ereignisse analysiert und auf der Grundlage der gewonnenen Erkenntnisse ein Modell erstellt.
-
Stell dir einen Wahrscheinlichkeitstheoretiker vor, der ein Kartenspiel spielt, bei dem er eine zufällige Karte aus dem gesamten Kartenspiel auswählt, wobei er weiß, dass nur Pik gewinnt, mit einer vorbestimmten Wahrscheinlichkeit. Unter der Annahme, dass der Kartensatz vollständig ist und die Auswahl völlig zufällig und gerecht ist, folgert er, dass die Wahrscheinlichkeit gleich
¼ist und kann eine Wette abschließen. -
Ein Statistiker wird das Spiel zunächst eine Zeit lang beobachten, um zu prüfen, ob das Spiel tatsächlich fair ist. Nachdem er (mit akzeptabler Annäherung) festgestellt hat, dass sich das Spiel lohnt, wird er den Wahrscheinlichkeitstheoretiker fragen, was er tun sollte, um zu gewinnen.
Statistik innerhalb einer großen Gruppe von Personen – Zufallsstichproben
Du hast sicherlich schon einige Wahlumfragen gesehen und dich gefragt, wie sie im Vergleich zu den Endergebnissen so genau sein können, auch wenn die Zahl der Befragten viel geringer ist als die Gesamtbevölkerung – das ist der Zeitpunkt, das Konzept einer Zufallsstichprobe einzuführen.
Der Grundgedanke bei einer Stichprobe ist, dass die Probanden nach dem Zufallsprinzip mit einer vorher festgelegten Wahrscheinlichkeit ausgewählt werden. Man kann zwischen mehreren Arten von Stichprobenverfahren unterscheiden:
- einfache Zufallsstichproben,
- Cluster-Stichproben,
- systematische Stichproben,
- Stichprobenverfahren mit größenabhängiger Auswahlwahrscheinlichkeit,
- geschichtete Zufallsstichproben,
- Minimax Stichproben,
- willkürliche Stichproben,
- Quotenstichproben,
- freiwillige Stichproben,
- Panelstichproben,
- Schneeballverfahren,
- Line-Intercept-Verfahren und
- theoretisches Sampling.
Jede dieser Methoden hat ihre Vor- und Nachteile, wobei die meisten von ihnen zufriedenstellend sind. Wesentliche Vorteile der Zufallsstichprobe sind die Zeitersparnis und die Kosteneffizienz, da nur eine begrenzte Anzahl von Personen befragt werden muss. Die Einfachheit dieses Verfahrens erfordert keine Fachkenntnisse und kann ohne umfangreiche Vorbereitung durchgeführt werden.
Praktische Anwendung der Wahrscheinlichkeitsrechnung
Es gibt viele Bereiche, in denen die Wahrscheinlichkeitstheorie angewendet wird. Es können Spiele mit einem hohen Zufallsfaktor, wie das Würfeln oder das Auswählen eines farbigen Balls aus Bällen mit 10 verschiedenen Farben sein, oder verschiedene Kartenspiele. Lotterien und Glücksspiele sind Spielen, bei denen das Konzept der Wahrscheinlichkeit und der allgemeine Wissensmangel bei diesem Thema ausgenutzt werden. Natürlich gewinnt von Zeit zu Zeit jemand, aber die Wahrscheinlichkeit, dass du es sein wirst, ist leider extrem gering.
Die Wahrscheinlichkeitstheorie wird auch bei vielen anderen Problemen angewendet. Vor allem bei Investitionen lohnt es sich, das Risiko zu berücksichtigen, um die beste Option zu wählen.
Unser Weiße Weihnachten Rechner 🇺🇸 verwendet historische Daten und die Wahrscheinlichkeitstheorie, um das Auftreten einer Schneedecke in der Weihnachtszeit für viele Städte vorherzusagen.
Wie berechne ich die Wahrscheinlichkeit von A und B?
Wenn A und B unabhängige Ereignisse sind, werden ihre Wahrscheinlichkeiten miteinander multipliziert, um die Wahrscheinlichkeit zu erhalten, dass sowohl A als auch B eintreten. Wenn die Wahrscheinlichkeit von A beispielsweise 20% (0,2) ist und die Wahrscheinlichkeit von B 30% (0,3) beträgt, ist die Wahrscheinlichkeit, dass beide Ereignisse eintreten, 0,2 ∙ 0,3 = 0,06 = 6%.
Wie berechne ich die bedingte Wahrscheinlichkeit?
Um die bedingte Wahrscheinlichkeit von A gegeben B zu berechnen:
- Bestimme die Wahrscheinlichkeit von B, d. h. P(B).
- Bestimme die Wahrscheinlichkeit von A und B, d. h. P(A∩B).
- Teile das Ergebnis von Schritt 2 durch das von Schritt 1.
- Fertig! Die Formel lautet: P(A|B) = P(A∩B) / P(B).
Wie hoch ist die Wahrscheinlichkeit, 2 Sechsen zu würfeln?
Wenn du mit fairen Würfeln würfelst, ist die Wahrscheinlichkeit, mit beiden Würfeln die Augenzahl Sechs zu würfeln, 1/6 ∙ 1/6 = 1/36 = 0,027 = 2,7 %. Das bedeutet, dass du 36 Mal würfeln musst, um erwarten zu können, dass du mindestens einmal 2 Sechsen würfelst. Da es um Wahrscheinlichkeiten geht, gibt es natürlich keine Garantie.
Wie drücke ich Chancen als Prozent aus?
Wandle die Chancen in eine Dezimalzahl um und multipliziere sie dann mit 100. Wenn die Chancen beispielsweise 1:9 stehen, ist ihre Dezimalform 1/9 = 0,1111. Multipliziere dieses Ergebnis dann mit 100, um 11,11% zu erhalten.