Calculadora del área superficial de prismas rectangulares

Te damos la bienvenida a la calculadora del área superficial de prismas rectangulares, donde tendrás la oportunidad de aprender todo sobre tu prisma de forma rápida y sencilla. En concreto, te explicaremos cómo hallar el área superficial de un prisma rectangular. ¿Quieres pintar un granero y te preguntas “cuánta pintura necesito 🇺🇸”? ¿O estás construyendo una piscina en tu jardín y quieres saber cuántas baldosas necesitarás?

No importa cuál sea la pregunta, siempre que se reduzca a “cuál es el área superficial de un prisma rectangular”, ¡este será el lugar adecuado!

Antes de ver cuál es el área superficial de un prisma rectangular, debemos familiarizarnos con el propio prisma.

Imagina una caja. Una caja normal y rectangular, como las que ves en el supermercado, llena de cualquier producto. Pues bien, ¡eso es un prisma rectangular! ¿O recuerdas aquellos dibujos de casas que hacíamos en preescolar? Cambia el tejado angular por uno plano, y te quedará otro ejemplo de prisma rectangular.

Formalmente (matemáticamente), un prisma rectangular recto es un sólido en el que las seis caras son rectángulos perpendiculares entre sí. Observa que esto, en concreto, significa que hay tres pares de caras idénticas situadas en lados opuestos del sólido.

Además, como en cualquier otra definición científica, hay algunos nombres extravagantes asociados al prisma. Las caras inferior y superior de la caja se llaman "bases", y a cada una de las otras cuatro se les denomina “cara lateral”. Por último, los lados de cada rectángulo se llaman aristas (de nuevo, divididas en “aristas de la base” y “aristas laterales”).

Pero dejemos a un lado las palabras altisonantes y centrémonos en cómo hallar el área superficial de un prisma rectangular.

Para saber cuál es el área superficial de un prisma rectangular, necesitamos conocer sus tres lados. Empecemos por la notación que utilizamos para ellos y para los demás valores en nuestra calculadora de área de prismas rectangulares:

• l - la longitud de la primera arista de la base;
• w - la longitud de la segunda arista de la base;
• h - la longitud de la arista lateral (también llamada alto o altura del prisma);
• A_b - el área de la base del prisma;
• A_l - el área lateral del prisma;
• A - el área superficial del prisma; y
• V - el volumen del prisma.

Observa que A_b denota el área superficial de una única base de nuestro prisma. En cambio, A_l denota el área lateral, es decir, el área total de las cuatro caras laterales. Por tanto, como el sólido tiene dos bases (la inferior y la superior), la fórmula del área superficial de un prisma rectangular es la siguiente:

área_superficial = 2 × área_de_la_base + área_lateral,

que, en nuestra notación, se traduce en:

A = 2 × A_b + A_l.

Recordemos que todas las caras de nuestra calculadora son rectángulos y, como se menciona en la calculadora del área de rectángulos, se calculan multiplicando las longitudes de los lados. Ahora, utilicemos esa información para estudiar la base de nuestro prisma. Con nuestra notación, la base es un rectángulo de lados l y w, por lo que su área es l × w. Y esa es precisamente la fórmula del área de la base:

A_b = l × w.

Pan comido, ¿verdad? Pues ahora vamos a intentar hacer algo un poco más complicado y pasar al área lateral. Tenemos cuatro caras que contribuyen a ese número, y todas ellas son rectángulos. Es más, entre las cuatro, hay dos pares de caras idénticas (la frontal y la trasera, y la izquierda y la derecha). Todas ellas tienen un lado igual a h, que es la longitud de la arista lateral (o su alto) del prisma. Además, el otro lado de uno de los pares es igual a la primera arista de la base, digamos l, y el otro es igual a la longitud de la segunda, que es w. En total, obtenemos que el área lateral, o A_l como la llamamos, es:

A_l = l × h + l × h + w × h + w × h,

o simplemente:

A_l = 2 × l × h + 2 × w × h.

Observa que, junto con el área de la base, esto nos permite obtener la forma final de la fórmula del área superficial de un prisma rectangular:

A = 2 × A_b + A_l = 2 × l × w + 2 × l × h + 2 × w × h.

Supongamos que intentas embaldosar una piscina y quieres saber el área superficial que tienes que embaldosar. Si la piscina es rectangular con fondo plano, ¡entonces lo que tenemos entre manos es precisamente un prisma rectangular! Veamos una bonita imagen para verlo con claridad.

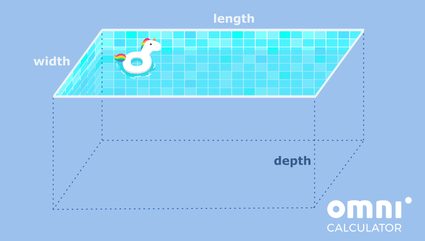
Vale, sabemos que es difícil apartar la vista del unicornio flotante, ¡pero volvamos al problema que nos ocupa!

Digamos que la piscina tiene un largo de 8 metros, un ancho de 6 metros, y una profundidad de 5 metros. Ahora que tenemos los números, intentemos ponerlos en términos de la notación que hemos utilizado antes.

En primer lugar, los lados de la base de nuestra piscina son su largo y su ancho, que en nuestro caso son 8 metros y 6 metros, respectivamente. Como estamos utilizando l y w como aristas de la base, podemos utilizar estos números en la calculadora anterior y establecer l = 8 metros y w = 6 metros. Ten en cuenta que no importa en qué orden los pongamos; solo se traduce en mirar la piscina desde otro ángulo y no cambia su área superficial.

Nos queda la profundidad de nuestra piscina y el número h de la calculadora. Y eso es exactamente lo que debemos hacer ahora: poner h = 5 m, que es la profundidad de la piscina o el alto del prisma.

“Y ya hemos acabamos, ¿verdad?” Bueno, no exactamente. La calculadora del área de un prisma rectangular nos da la respuesta:

A = 2 × l × w + 2 × l × h + 2 × w × h = 2 × 8 m × 6 m + 2 × 8 m × 5 m + 2 × 6 m × 5 m = 236 m².

Pero esa es el área superficial de todo el prisma, y no queremos embaldosarlo 🇺🇸 por todas partes. Después de todo, si embaldosamos la parte superior, sería bastante difícil entrar (o salir), ¿no? Eso sí que sería maldad de alto nivel, incluso peor que cuando le quitamos la escalera a la piscina de los Sims.

Para encontrar la respuesta correcta, pasemos al modo avanzado, que nos permite ver el área de la base y el área lateral del sólido. Ya que sabemos hallar él área superficial de un prisma rectangular (A):

A = 2 × A_b + A_l,

solo tenemos que restarle el área extra que no estamos embaldosando. Y eso es la parte superior. Pero la base superior es la misma que la inferior, así que el área que necesitamos embaldosar es, de hecho:

Área a embaldozar = A - A_b,

que, en nuestro caso, es:

Área a embaldozar = 236 m² - 48 m² = 188 m².

Ahora estás un paso más cerca de terminar la piscina y poder admirar tu trabajo mientras disfrutas de una cerveza fría. Dicho esto, el prisma no es la única forma tridimensional con base rectangular; descubre más en la calculadora del área de una pirámide rectangular 🇺🇸.