Calculadora del coeficiente binomial

Bienvenido a la calculadora del coeficiente binomial, donde podrás calcular y aprender todo sobre la misteriosa fórmula de combinaciones de n en k. La expresión denota el número de combinaciones de k elementos que hay de un conjunto de n elementos y corresponde al botón nCr de una calculadora de la vida real.

Para la respuesta a la pregunta "¿Qué es un binomio?", el significado de combinación, la solución a "4 en 2" y la comparación de permutación frente a combinación, ¡adelante y desplázate a las secciones de abajo!

En matemáticas (álgebra para ser precisos), un binomio es un polinomio con dos términos (de ahí viene el prefijo "bi-"). Por ejemplo, las expresiones x + 1, xy - 2ab o x³z - 0.5y⁵ son todas binomios, pero x⁵, a + b - cd o x² - 4x² no lo son (la última sí tiene dos términos, pero podemos simplificar esa expresión a -3x², que solo tiene uno).

Ahora que sabemos lo que es un binomio, veamos más detenidamente como elevar uno de ellos a una potencia:

(x² - 3)³.

Hay algunos casos especiales de esa expresión: las fórmulas de multiplicación abreviada que quizá conozcas de la escuela:

(a + b)² = a² + 2ab + b²,

(a - b)² = a² - 2ab + b².

El polinomio que obtenemos en el lado derecho se llama la expansión binomial de lo que teníamos entre paréntesis. Lo creas o no, podemos encontrar sus fórmulas para cualquier potencia entera positiva. En todos los casos, el teorema del binomio nos dice cómo es esta expansión:

donde:

• $C_k$ es el número de todas las combinaciones posibles de $k$ elementos de un conjunto de $n$elementos.

Además, para un n dado, estos números se presentan ordenadamente para valores consecutivos de n en las filas del llamado triángulo de Pascal, donde una fila entera cuenta todos los subconjuntos posibles del conjunto total (es decir, la cardinalidad del conjunto potencia). Visita nuestra calculadora del triángulo de Pascal 🇺🇸 para generar el triángulo de Pascal del tamaño que elijas.

Y éste es un buen momento para que comprobemos el significado de "combinación", como ya hemos mencionado tantas veces.

Imagina que eres un estudiante universitario, echándote una siesta casual durante una clase. De repente, el profesor te devuelve a la realidad diciendo: "Vamos a elegir los grupos para los proyectos parciales al azar". Y bueno, parece que, después de todo, tendrás que hacer algún trabajo.

El problema es que solo hay una persona con la que te gustaría trabajar en el proyecto. Si hay veinte personas en el grupo, y el profesor los divide en grupos de cuatro, ¿qué probabilidad hay de que tengas suerte?

Cada grupo posible es un ejemplo de combinación. En este caso, una combinación de cuatro elementos de un conjunto de veinte elementos, o, si lo prefieres, de cuatro alumnos de un grupo de veinte personas. Si quieres ponerte un poco técnico, elegir una combinación significa elegir un subconjunto de un conjunto mayor. Lo más importante aquí es que el orden de los elementos que elijamos no importa. Al fin y al cabo, todos los miembros de un equipo son iguales (excepto los que no hacen ningún trabajo).

El número de combinaciones de k elementos de un conjunto de n elementos se denota por

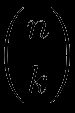
(como una fracción de n dividida por k pero sin la recta intermedia) que leemos como "n en k" También es el símbolo que aparece cuando elegimos pulsar nCr en una calculadora (no en nuestra calculadora de coeficiente binomial, sino en una calculadora clásica de la vida real). Por ejemplo,

es "6 sobre 2" o "6 en 2". En algunos libros de texto, el coeficiente binomial también se denota por C(n,k), por lo que es una función de n y k. "¿Y cómo lo calculo?" Pues muy fácil. La fórmula de n en k es

n! / (k! × (n - k)!).

El signo de exclamación se llama factorial. La expresión n! es el producto de los primeros n números naturales, es decir,

n! = 1 × 2 × 3 × ... × n.

Esto significa que, por ejemplo, el 4 en 2 de arriba es

4! / (2! × (4 - 2)!) = (1 × 2 × 3 × 4) / (1 × 2 × 1 × 2) = 6,

y 6 en 2 es

6! / (2! × (6 - 2)!) = (1 × 2 × 3 × 4 × 5 × 6) / (1 × 2 × 1 × 2 × 3 × 4) = 15.

Para saber más sobre factoriales, ¡visita nuestra calculadora de factoriales 🇺🇸!

Así que podemos elegir dos elementos de un conjunto de cuatro, de hasta seis formas distintas y de un conjunto de seis, hasta de quince formas.

Antes de seguir adelante, echemos otro vistazo a la fórmula n en k. Podemos obtener de ella una propiedad simétrica bastante interesante.

Si tomamos n y elegimos n - k, obtendremos

n! / ((n - k)! × (n - (n - k))!) = n! / ((n - k)! × k!)

que es lo mismo que n sobre k (ya que la multiplicación es conmutativa). En otras palabras, tenemos

o C(n,k) = C(n,n-k) en la otra notación.

En la sección anterior, hemos visto qué es un factorial. En combinatoria, el factorial denota el número de permutaciones. Una permutación de longitud n significa poner n elementos en cierto orden. Por ejemplo, si tenemos tres expresiones de gatitos monos, digamos 😹, 😻 y 🙀, podemos ordenarlas de seis formas distintas:

(😹, 😻, 🙀)

(😹, 🙀, 😻)

(😻, 😹, 🙀)

(😻, 🙀, 😹)

(🙀, 😹, 😻)

(🙀, 😻, 😹).

Observa que esto coincide con lo que nos dice el factorial:

3! = 3 × 2 × 1 = 6.

Visita nuestra calculadora de permutaciones 🇺🇸 para profundizar más.

Observa que también podemos entender esta fórmula así: elegimos el primer elemento de entre tres (3 opciones), el segundo de entre los dos que quedan (porque ya hemos elegido una, quedan 2 opciones), y el tercero nos viene dado (porque ya hemos elegido dos, queda 1 opción). Multiplicamos el número de opciones: 3 × 2 × 1 = 6, y obtenemos el factorial.

Cuando comparamos permutación frente a combinación, la palabra clave es orden. Como hemos dicho en la sección anterior, el significado de una combinación es elegir unos pocos elementos de una colección mayor. En esencia, decimos cuáles elegimos, pero no cuál es el primero, el segundo, etc. Forman un conjunto.

Una permutación, sin embargo, pone los elementos en un orden fijo, uno detrás de otro, lo que la convierte en una sucesión y no en un conjunto. Además, una permutación utiliza todos los elementos del conjunto que hemos tenido, mientras que una combinación solo elige algunos de ellos.

Como ejemplo, una vez más, ponte en el lugar del estudiante universitario. Cuando el profesor eligió el grupo para ti, eligió una combinación. Y cuando llega el momento de presentar vuestro proyecto, y os hace una pregunta a cada uno, elige una permutación (determinando el orden en que os hace las preguntas). Y todos sabemos lo importante que puede ser el orden para tu nota final.

Los coeficientes binomiales son una de las sucesiones numéricas más importantes de las matemáticas discretas y la combinatoria. Aparecen muy a menudo en estadística y cálculos de probabilidad, y quizá sean los más importantes en la distribución binomial (incluida la distribución binomial negativa 🇺🇸). ¿Significa eso que solo los matemáticos frikis tienen un uso real para ello?

¡En absoluto! Todo juego de azar se basa en la suerte, y los coeficientes binomiales son el jugador vital. Un simple lanzamiento de moneda es el ejemplo más sencillo, que puedes calcular con nuestra calculadora de probabilidad de cara o cruz. Sin embargo, vayamos un paso más allá y fijémonos en el póquer.

¿Te has preguntado alguna vez por qué algunas manos o juegos en el póquer son más valiosas que otras? Sencillamente porque son más raras (a menos que alguien haga trampas, pero hemos visto suficientes series de televisión de gángsters como para saber que eso suele ser una mala idea).

Hay 52 cartas en una baraja normal, y en Texas hold 'em, un jugador recibe cinco cartas. Nuestra calculadora de coeficiente binomial y la fórmula n en k (en nuestro caso con n = 52 y k = 5) nos dice que esto se traduce en 2 598 960 manos posibles en una partida de póquer. Bastante, ¿no crees? Y ahora considera la mejor mano posible: una escalera real de tréboles (As, Rey, Reina, Jota y 10). Esta mano puede ocurrir solo en un caso: cuando tenemos exactamente esas cartas. Esto significa que hay una 1 entre 2 598 960 posibilidades de tenerla. No te recomendamos que apuestes todos tus ahorros a esas probabilidades.

Tomemos otro ejemplo: un full (un trío y una pareja). Esta vez hay considerablemente más posibilidades. Al fin y al cabo, cualquiera de las 13 cartas de un palo puede ser el trío, y la pareja está en una de las otras 12 cartas (no puede ser del mismo valor que el triple). Además, el trío solo está en tres de los cuatro símbolos de cartas, y la pareja solo está en dos.

¡Y ahí es donde recordamos el significado de una combinación! Tenemos que elegir tres de cuatro símbolos para el triple y una combinación de dos de cuatro para la pareja. La fórmula n en k traduce esto en 4 en 3 y 4 en 2, y la calculadora del coeficiente binomial muestra que son 4 y 6, respectivamente. En definitiva, si ahora multiplicamos los números que hemos obtenido, veremos que hay

13 × 12 × 4 × 6 = 3744

manos posibles que dan un pleno. Bueno, no demasiadas comparadas con todas las posibilidades, pero al menos es 3744 veces más probable que la escalera real de tréboles.

Aun así, sugerimos ahorrar dinero regularmente como mejor técnica de inversión que apostar.