Calculadora de crecimiento exponencial

Existe un número considerable de procesos para los que puedes utilizar esta calculadora de crecimiento exponencial. La regla general es que la fórmula de crecimiento exponencial:

se utiliza cuando existe una cantidad con un valor inicial, $x_0$, que cambia a lo largo del tiempo, $t$, con una tasa de cambio constante, r. La función exponencial que aparece en la fórmula anterior tiene una base igual a 1 + r/100.

Ten en cuenta que la tasa de crecimiento exponencial, $r$, puede ser cualquier número positivo, aunque esta calculadora también funciona como una calculadora de decrecimiento exponencial (también conocido como decaimiento exponencial), donde $r$ también representa la tasa de decrecimiento (la cual debe estar entre 0 y -100 %). Esta restricción se debe a que no se puede tener un decrecimiento superior al 100 % con respecto a la cantidad inicial, ya que daría como resultado un valor negativo.

La ecuación de crecimiento exponencial se utiliza en datación por radiocarbono 🇺🇸, PCR (puedes descubrir por qué con nuestra calculadora de temperatura de recocido 🇺🇸), así como en el cálculo del interés compuesto. A continuación encontrarás más ejemplos del uso de esta fórmula.

Consideremos el siguiente problema: la población de una pequeña ciudad a principios de 2019 era de 10 000 personas. Se observa que la población de la ciudad crece a un ritmo constante del 5 % anual. ¿Qué deberías hacer para calcular el tamaño a futuro de la población en el año 2030? A partir de los datos previos, podemos concluir que el valor inicial de la población, $x_0$, es igual a 10 000. Además, tenemos una tasa de crecimiento de $r = 5\ \%$.

Por lo tanto, la fórmula de crecimiento exponencial que debemos utilizar es:

Aquí $t$ es el número de años transcurridos desde 2019. En nuestro caso, para el año 2030, debemos utilizar $t = 11$, ya que esta es la diferencia en el número de años entre 2030 y el año inicial 2019. Finalmente, obtenemos:

Así pues, el número previsto de habitantes de nuestra pequeña ciudad en el año 2030 es de unos 17 103.

Si quieres profundizar un poco más en esta fórmula, puedes utilizar nuestra calculadora de crecimiento exponencial para averiguar el número de habitantes previsto para cada año, a partir de 2019. Este cálculo da como resultado la siguiente tabla, en la que redondeamos los resultados al número entero más próximo:

Si quieres tener una idea aún más clara del crecimiento de la población, puedes representar estos datos gráficamente, siendo el eje horizontal el eje temporal (t) y el eje vertical el valor de la población $x(t)$. Los datos de la tabla son todos los puntos situados en el gráfico de la función de crecimiento exponencial:

Como la base de esta función exponencial es 1.05, y como es mayor que 1, el gráfico de crecimiento exponencial que obtenemos es creciente. La principal diferencia entre este gráfico y el de la función exponencial normal es que su corte con el eje y no está en 1, sino en 10 000, que corresponde al valor inicial $x_0$:

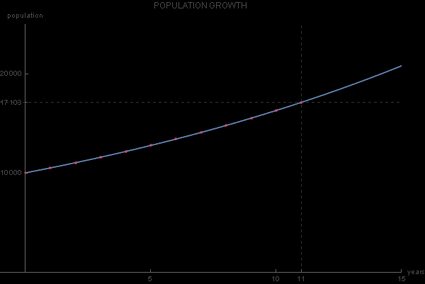
A partir de este ejemplo, podemos ver las posibles limitaciones del modelo de crecimiento exponencial: es poco realista que la tasa de crecimiento se mantenga constante a lo largo del tiempo. De hecho, es difícil esperar que la tasa de crecimiento anual de la población de la ciudad se mantenga en el 5 % durante una década o más.

En la vida real, se producen oscilaciones naturales de la tasa de crecimiento que no se incluyen en este modelo de crecimiento exponencial. Un modelo más realista para el crecimiento de una población es el modelo de crecimiento logístico, que cuenta con una capacidad de carga o sustentación, una constante que representa el límite de crecimiento natural de la población.

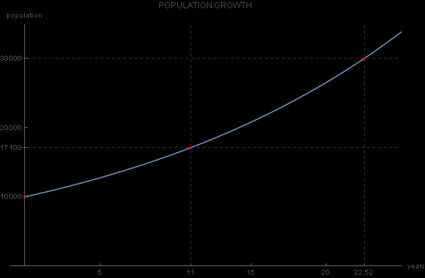
Siguiendo con nuestra pequeña ciudad, la siguiente pregunta que puedes hacerte es: "¿cuándo podemos esperar que la población alcance algún valor importante?" Esto es útil si se quiere saber cuándo ajustar el planeamiento urbanístico de la ciudad a una población mayor, de modo que el gobierno local pueda saber en qué año la población de la ciudad se triplicará con respecto a los 10 000 habitantes originales…

Aquí, sabemos cuánto es $x(t)$, pero desconocemos el valor de t cuando esto ocurra. Vayamos paso a paso:

1. Inserta $x(t) = 30 000$ en la fórmula: $30\ 000 = 10\ 000 \cdot 1.05^{t}$

2. Después de dividir ambos lados de la ecuación por 10 000, obtenemos $1.05^{t} = 3$.

3. Tomamos el logaritmo en base 1.05 de ambos lados de esta ecuación: $t = \log_{1.05} 3$.

4. Usa el logaritmo para obtener finalmente: $t = 22.52$.

Así pues, la respuesta al interrogante del gobierno es aproximadamente 22 años después del año inicial (2019), es decir, en 2041:

Puede que ya te hayas dado cuenta de un problema con el crecimiento y decrecimiento exponencial, y es que, naturalmente, trata el tiempo sólo como un valor positivo, por lo que estamos prediciendo una cantidad futura. Sin embargo, esto no nos impide utilizar esta fórmula con valores negativos de tiempo. Esto significa que describimos el fenómeno de interés en el tiempo anterior a la observación inicial.

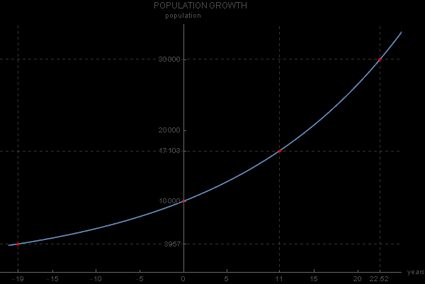
En el caso del crecimiento de la población, podemos preguntarnos: ¿cuál era la población de nuestra pequeña ciudad en el año 2000, suponiendo que la tasa de crecimiento de la población fuera de un 5 % constante?

Para responder a esto, se usaría $t = -19$, ya que el año 2000 precede al año 2019 en 19 años. Por lo tanto, la respuesta sería:

habitantes, como también puede verse en este gráfico:

Para algunas aplicaciones, como por ejemplo al calcular el decrecimiento exponencial de una sustancia radiactiva, resulta más productiva una forma alternativa de escribir la fórmula del crecimiento y decrecimiento exponenciales:

El coeficiente $k$ desempeña el papel de la tasa de crecimiento, de forma similar a como lo hace r en la fórmula original del crecimiento exponencial. Comparando la ecuación anterior con la original, se puede ver que la relación entre $r$ y $k$ es la siguiente:

lo que significa $r = 100 \cdot (e^k- 1)$ y $k = \ln(1 + r/100)$.

La desintegración radiactiva es un ejemplo bien conocido en el que se utiliza la fórmula de decrecimiento exponencial. Para una cantidad inicial dada de sustancia radiactiva, puedes escribir la ley que rige su desintegración a lo largo del tiempo. Pero, quizás, un ejemplo más divertido sea medir cuánto café queda en tu cuerpo a las 10 de la noche si bebiste una taza de café con $x_0 = 95\ \rm mg$ de cafeína al mediodía.

Utilizaremos el hecho de que la semivida de la cafeína en el cuerpo humano es de aproximadamente seis horas. La semivida se define como el tiempo que necesita una cantidad dada para reducirse a la mitad de su valor inicial. Así, en este ejemplo tenemos

$x(6) = 1/2 \cdot 95 \text{ mg} = 47.5 \text{ mg}$

Aquí, será más fácil utilizar la notación alternativa para la fórmula de crecimiento exponencial:

$x(t) = 95 \cdot e^{kt}$

He aquí el cálculo paso a paso:

1. Inserta x(6)= 47.5 y t = 6 en la ecuación: $47.5 = 95 \cdot e^{6k}$.

2. Esta expresión, después de dividir ambos lados de la ecuación por 95 y aplicar el logaritmo natural, da: $6 \cdot k = \ln 0.5$.

3. Aplicando el logaritmo natural, obtenemos: $k = -0.1155$.

4. Por lo tanto, la fórmula de decrecimiento exponencial en nuestro ejemplo es: $x(t) = 95 \cdot e^{-0.1155 \cdot t}$.

5. Dado que las 10 pm son diez horas más tarde que el mediodía, queremos saber la cantidad de cafeína en $t = 10$. Tenemos: $x(10) = 95 \cdot e^{-0.1155 \cdot 10} = 29.9305$.

Concluimos entonces que, a las 10 pm, la cantidad de cafeína que quedará en tu cuerpo será aproximadamente 30 mg.

El tiempo puede expresarse básicamente en cualquier unidad apropiada. Para algunos problemas, serán segundos, para otros, años. Debes elegir la unidad de tiempo de forma que se corresponda con la naturaleza del proceso observado. Por ejemplo, si quieres entender el cambio en la población de una ciudad, debes elegir años. Por otro lado, si vas a calcular la cantidad de café que queda en tu cuerpo después de beberte una taza, la unidad de tiempo apropiada debería ser horas o quizá minutos.

Ten en cuenta que $t$ no tiene por qué considerarse solo tiempo. En algunos casos, la variable que mide el índice de cambio puede ser distinta del tiempo. Por ejemplo, al estudiar la forma en que cambia la presión atmosférica con la altitud, la variable que mide este cambio es la distancia, y debes elegir los metros como unidades de cambio apropiadas. Nuestra calculadora de la presión atmosférica a diferentes alturas 🇺🇸 puede ayudarte en este caso.

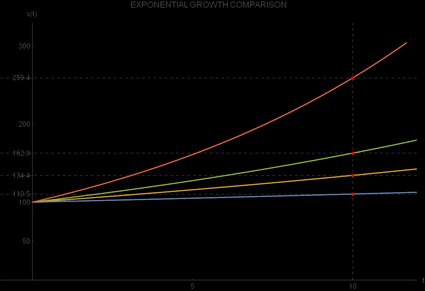
Distintas tasas de crecimiento exponencial r tendrán una influencia significativamente distinta en la rapidez con que la cantidad observada cambia con respecto al valor inicial. Empecemos con $x_0 = 100$ y, utilizando la calculadora de crecimiento exponencial, veamos cuál será $x(10)$ para cuatro valores diferentes de $r$:

En esta tabla, vemos que todos los valores iniciales son iguales, siendo $x_0 = 100$, pero los valores finales de $x(10)$ difieren significativamente. Tu intuición puede engañarte aquí, porque la diferencia entre el 1 % y el 3 % no parece grande, pero al cabo de diez periodos, el valor de $x(10)$ es un 21.67 % más alto para el crecimiento del 3 % en comparación al crecimiento del 1 %.

Si comparamos el crecimiento del 10 % con el crecimiento del 5 %, observaremos una diferencia aún mayor, del 59.23 %, a favor del crecimiento del 10 %. Puedes observar este contraste en la siguiente representación gráfica de las cuatro funciones de crecimiento exponencial:

La fórmula del crecimiento y decrecimiento exponenciales se utiliza para modelar diversos fenómenos del mundo real:

• crecimiento de la población de bacterias, virus, plantas, animales y personas,
• decaimiento de materia radiactiva,
• concentración de fármacos en sangre,
• presión atmosférica del aire a cierta altura,
• interés compuesto y crecimiento económico,
• datación por radiocarbono o
• poder de procesamiento de los ordenadores, etc.

How Populations Grow: The Exponential and Logistic Equations

Two Models of Population Growth

The World’s Population Hasn’t Grown Exponentially for at Least Half a Century

Exponential Population Growth

Caffeine Pharmacology

Caffeine Effects on Sleep Taken 0, 3, or 6 Hours before Going to Bed