Calculadora del número áureo

La calculadora del número áureo determinará la longitud de las partes en las que hay que dividir un segmento para obtener la razón áurea. Antes de pasar a calcular la proporción áurea, vamos a explicar en qué consiste. A continuación encontrarás toda la información que necesitas.

También puedes consultar la calculadora de proporciones 🇺🇸 si quieres aprender sobre proporciones en general.

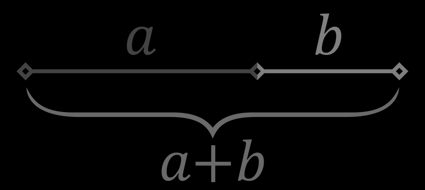
El número áureo (también conocido como razón áurea, proporción áurea o sección áurea) surge cuando un segmento se divide en dos partes: la proporción entre la parte más larga y la más corta debe ser la misma que la proporción entre el segmento entero y la parte más larga. Es decir, si la parte más larga tiene una longitud $a$ y la parte más corta tiene una longitud $b$, la fórmula de la proporción áurea es la siguiente:

Para calcular el valor de la proporción áurea, hay que resolver la ecuación anterior para $a/b$. Para esto, la reorganizamos como:

Así, al final, solo tenemos que resolver la ecuación cuadrática $x^2-x-1=0$ para obtener el valor de $x$. Al hacer esto descubrimos que el valor de la proporción áurea es igual a $\frac 12 (1+\sqrt{5})$, que es aproximadamente $1.61803398875...$. Este número se suele representar con la letra griega $\phi$.

Ya sabemos qué es la proporción áurea y cómo calcular su valor, así que ahora veamos cómo comprobar si dos longitudes dadas obedecen esta proporción.

Aquí tienes las instrucciones paso a paso que te ayudarán a comprobar si dos segmentos están en una proporción áurea:

1. Determina la longitud del segmento más largo y llámalo a.
2. Determina la longitud del segmento más corto y llámalo b.
3. Calcula a/b.
4. Si la proporción es (aproximadamente) igual a 1.618, tus segmentos están en proporción áurea.

También puedes utilizar la calculadora del número áureo de Omni para hacer el trabajo. Aunque cualquier calculadora de razones 🇺🇸 puede ayudarte con eso, nuestra calculadora del número áureo se ocupa específicamente de este tema, ¡así que no encontrarás una mejor herramienta!

La calculadora del número áureo de Omni no podría ser más sencilla y directa de usar. Tiene tres campos, correspondientes a las tres longitudes que aparecen en la fórmula de la proporción áurea. Basta con introducir uno de ellos para que los otros dos se calculen automáticamente. ¿Fantástico, no?

El rectángulo dorado (o rectángulo áureo) es un rectángulo cuyas longitudes laterales obedecen la proporción áurea, es decir, la relación entre su longitud y su anchura es de $1.618$. Este rectángulo se encuentra con frecuencia en el arte, ya que se cree que es el más agradable a la vista humana entre todos los rectángulos. La calculadora del rectángulo dorado 🇺🇸 es una forma práctica de encontrar los lados de un rectángulo dorado en lugar de calcularlos a mano.

El número áureo siempre ha tenido una relevancia especial en la ciencia y el arte gracias a sus propiedades y apariencia. Si hablamos de matemáticas:

• Un rectángulo dorado puede dividirse en dos rectángulos áureos más pequeños (mantiene sus proporciones).
• La proporción áurea está estrechamente relacionada con el número "5". Este número aparece en su definición (φ = (1 + √5)/2) y en los pentágonos como la relación entre la diagonal y el lado.

En el arte, la proporción áurea apareció más recientemente: D2/.alí, por ejemplo, utilizó esta proporción en muchas de sus obras.

Muchas fuentes históricas y contemporáneas afirman que la proporción áurea está ampliamente presente en la naturaleza. Algunos ejemplos son:

• el patrón de crecimiento de las hojas;
• las superficies geométricas de algunas verduras y conchas marinas; y
• las proporciones de los huesos de algunos animales.

Sin embargo, si bien no podemos negar la presencia de patrones geométricos en la naturaleza, no podemos confirmar la exactitud de las proporciones de los ejemplos anteriores: algunos presentan enormes variaciones, mientras que otros solo se aproximan a la proporción áurea.