CAPM Calculator – Capital Asset Pricing Model

This capital asset pricing model calculator or CAPM formula helps you find out the expected return of your asset or investment according to its inherent risk level.

If you already know how to calculate CAPM, you may have a look at our weighted average cost of capital calculator, which helps you to calculate a firm's cost of capital with also taking into account the debt dimension of an investment.

The CAPM (capital asset pricing model) is one of the foundational models in finance designed to specify the appropriate required rate of return of a financial asset or investment (see the rate of return calculator for more).

Considering that CAPM is mainly applied to financial assets (securities), we will focus on these types of assets in the following discussion.

Since the core of the CAPM model is the "beta" parameter, the most widely employed financial measure used by academic researchers and practitioners, we shall get a bit more insight into its function.

The starting point is that the CAPM model is based on the perception that we can separate the total risk of a particular asset into two distinct parts:

• Market risk, undiversifiable market risk or systematic risk, assigned by “beta”, measures the variation of asset value in response to a change in the aggregated value of all assets in the economy.

• Specific risk or diversifiable risk, which can be attributed to the peculiarity of an asset and its close environment.

The below graph represents the alteration of these risks depending on the number of assets in the portfolio.

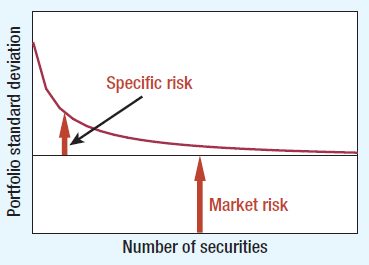
On the graph, you can see that the specific risk, unlike the market risk, can be reduced by increasing the number of assets included in the portfolio; more precisely, this type of risk can be eliminated by diversification. Therefore, according to the CAPM model, the required rate of return should depend on its market risk or "beta": the higher systematic risk should imply a higher expected return for the asset.

Wise investors don't take risks just for fun, right? Since they play with real money, they require a higher return from the market portfolio than from a risk-free asset. More specifically, according to the CAPM, the required rate of return equals the risk-free interest rate plus a risk premium that depends on beta and the market risk premium.

We can illustrate these relations with the CAPM formula:

• risk premium = beta × (market risk premium)

• market risk premium = Rm - Rf

To get a better insight, the graph below displays the visual representation of the CAPM equation.

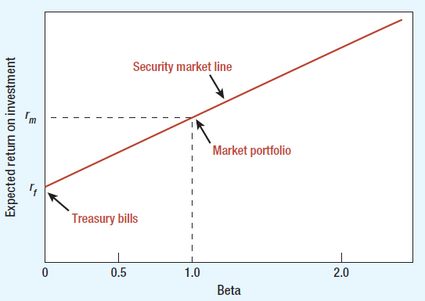
You can see on the graph that the intercept of the beta of 1 and the market return represents the market portfolio. It means that a well-diversified portfolio with such assets moves together with the market.

A beta of 0.5 has below-average market risk, which means that a well-diversified portfolio of these assets tends to be half as sensitive to market changes.

Since the expected risk premium on each investment is proportional to its beta, each investment should lie on the sloping security market line, which connects the risk-free return (treasury bills on the graph) and the market portfolio.

If you want to calculate the CAPM for your asset or investment, you need to use the following CAPM formula:

R = Rf + risk premium

risk premium = beta × (Rm - Rf),

where:

• R – Expected rate of return of an asset or investment;
• Rf – Risk-free interest rate, typically taken as the yield on a long-term government bond in the country where the project is based;
• Rm – Broad market return; and
• Beta – Parameter of the market risk.

To demonstrate the mechanism of the CAPM model more vividly, it might be worth looking at a real-world example.

Let's say you are a shareholder considering investing in a particular stock to widen your portfolio, and you would like to evaluate the effect of the new share on your portfolio.

Let's recall the CAPM formula:

R = Rf + beta × (Rm - Rf)

Since Treasury bills are typically considered a risk-free investment, we can use its yield for the calculation, thus Rf = 2.4% for the 3-month US Treasury Bill.

Because calculation behind the parameter beta involves more in-depth research with some statistics, we will rely on a published average value of beta of a well-known company, Walmart Inc. Therefore, beta = 0.47 means that the sensitivity of Walmart share's return for changes in the aggregate value of assets share is around half of the average market.

The last variable which we need for the calculation is the market return. In the case of stocks, to estimate the market return, we can use the long-term average return of the S&P 500 or the Dow Jones, which can be considered an index to reflect the overall return characteristic of the stock market. For the S&P 500, since its initiation in 1928 through to 2017, its average yearly return is 10%, so Rm = 10%.

Substituting the values into the CAPM formula, we attain the following:

R = 2.4 + 0.47 × (10 - 2.4) = 5.97

Notice that the market risk premium is 7.6%, and the risk premium of a Walmart share is 3.57%.

Thus, with rounding, R = 6%, which means that an expected return of a Walmart share is around 6%.

Recognize also that if we assume that the beta of your initial portfolio was more than 0.47, widening your portfolio by Walmart shares lowers the beta of the new portfolio. In other words, it reduces the reactiveness of the new portfolio's return to aggregate changes in the economy.

• William Sharpe, who designed the Sharpe ratio also, was awarded the Nobel Prize in Economics in 1990 for the development of the Capital Asset Pricing Model (CAPM). In 2002, this prize was given to Daniel Kahneman for developing the Prospect Theory (PT), which contradicts the Expected Utility Theory (EUT) on which the CAPM is based. Learn more by visiting our Sharpe ratio calculator

• Since the CAPM model strictly relies on assumptions about investor behaviors, risk and return distribution, and market fundamentals which often depart from the reality, CAPM is heavily criticized both theoretically and empirically. Still, understanding the concept behind the CAPM model can help you to perceive the relationship between risk and return and to become a smarter investor.