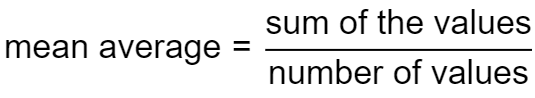Calculateur de moyenne arithmétique

Le calculateur de moyenne arithmétique peut trouver la moyenne d'une liste de nombres donnés, jusqu'à un maximum de trente. Un aspect intéressant de notre calculateur est de pouvoir voir la moyenne évoluer au fur et à mesure que vous entrez des valeurs. Mais avant d'expliquer le fonctionnement du calculateur de moyenne arithmétique plus en détail, nous allons vous apprendre à calculer cette dernière à la main. Cela vous sera utile si vous n'avez pas accès à Internet et que vous ne pouvez plus vous rendre sur Omni Calculator. Notez que pour ce calculateur, nous ne ferons pas de distinction entre les termes moyenne arithmétique et moyenne tout court.

Pour calculer la moyenne d'un ensemble de nombres, il suffit de les additionner et de diviser le résultat par le nombre de valeurs. Par exemple, calculons la moyenne de 24,55, 17, 87 et 100. Tout d'abord, additionnons-les : 24 + 55 + 17 + 87 + 100 = 283. Divisons ensuite 283 par 5 pour obtenir 56,6. Ce calcul peut être effectué à la main pour les ensembles de nombres simples, mais il est plus pratique d'utiliser notre calculateur pour les nombres complexes ou ceux avec de nombreuses décimales. Le calculateur de notes moyennes 🇺🇸 effectue un calcul similaire. Il détermine la moyenne de notes, de votes ou d'avis, en prenant en compte les valeurs de 1 à 5.

Le calculateur de moyenne pondérée 🇺🇸 vous permet d'attribuer des pondérations à chaque nombre. La pondération d'un nombre est un indicateur de son importance. Un type courant de moyenne pondérée est la moyenne générale. Par exemple, aux États-Unis, on parle de GPA (angl. Grade Point Average, moyenne pondérée cumulative). Le GPA a une échelle de notation de A, B, C, D et F. Chaque note se voit attribuer un certain nombre de points. Une note A reçoit 4 points, un B=3, un C=2, un D=1 et un F=0. Alors, si vous souhaitez partir étudier aux USA ou si vous êtes tout simplement curieux·se, n'hésitez pas à jeter un œil à notre calculateur de GPA 🇺🇸. Pour effectuer ce calcul à la main, suivez ces étapes :

1. Multipliez la valeur de la note par le nombre de crédits du cours.
2. Effectuez cette opération pour tous les cours et faites la somme.
3. Divisez la somme par le nombre total de crédits.

Supposons que les notes soient un A pour un cours de 3 crédits, deux B pour un cours de 4 crédits et un C pour un cours de 2 crédits. Donc, comme mentionné plus haut, en attribuant la valeur de 4 pour un A, 3 pour un B et 2 pour un C, la moyenne générale est la suivante :

GPA = [4×3 + 3×4 + 3×4 + 2×2]/(3 + 4 + 4 + 2) = 40/13 = 3,08

Notez que le calculateur de moyenne arithmétique calculera la moyenne pour toutes les valeurs qui sont pondérées de manière égale, contrairement aux outils mentionnés ci-dessus. En statistique, la moyenne est considérée comme une mesure de la tendance centrale.

Il existe quatre types de moyennes : la moyenne arithmétique, la médiane, le mode et l'étendue. La moyenne arithmétique est la moyenne la plus courante et celle que l'on appelle tout simplement moyenne par abus de language. On la calcule en additionnant toutes les valeurs d'un ensemble et en divisant la somme par le nombre de valeurs. La médiane est la valeur centrale d'un ensemble. Si l'ensemble est pair, on calcule la moyenne des deux valeurs centrales. Le mode est la valeur qui apparaît le plus souvent dans un ensemble. L'étendue est la différence entre la valeur la plus élevée et la valeur la plus faible d'un ensemble.

Nous calculons des moyennes parce qu'elles sont une manière très utile de présenter une grande quantité de données. Au lieu d'avoir à parcourir des centaines ou des milliers de données, nous avons un chiffre qui résume succinctement l'ensemble. Bien que les moyennes posent certains problèmes, tels que les valeurs aberrantes qui donnent une moyenne inexacte, elles sont utiles pour comparer les données en un claquement de doigt.

Les moyennes ne sont pas toujours un reflet exact des données. Elles sont généralement utiles pour décrire des ensembles de données qui suivent une loi normale, en forme de cloche, où la plupart des valeurs se trouvent au milieu et où les valeurs extrêmes sont rares. Or, seulement un point très extrême suffit à modifier la moyenne de façon spectaculaire, de sorte que ces anomalies sont souvent exclues, mais pas toujours. Ensuite, l'être humain a tendance à interpréter les moyennes comme des représentations parfaites, ce qui nous conduit à ne pas toujours vouloir comprendre les nuances des données. Enfin, nous utilisons majoritairement les moyennes pour prédire des cas individuels, ce qui est souvent très imprécis.

Pour calculer votre moyenne générale :

1. Multipliez chaque note par les crédits, les coefficients, ou les pondérations qui lui sont attribués. Si vos notes ne sont pas pondérées, sautez cette étape.
2. Additionnez toutes les notes pondérées (ou seulement les notes s'il n'y a pas de pondération).
3. Divisez la somme obtenue par le nombre de notes additionnées.
4. Le quotient obtenu est votre moyenne finale.

Pour évaluer une moyenne pondérée :

1. Multipliez chaque nombre par sa pondération.
2. Additionnez tous les nombres pondérés.
3. Divisez la somme par le nombre de points de données.
4. Le quotient obtenu est la moyenne pondérée.

Il n'y a pas de réponse simple à la question de savoir si la moyenne arithmétique est meilleure que le mode. Cela dépend entièrement de l'ensemble de données que vous avez sous les yeux. Si les données sont normalement distribuées et ne présentent pas de valeurs aberrantes, vous devriez probablement utiliser la moyenne, car elle vous donnera la valeur la plus représentative. Le mode, en revanche, est plus stable et présente la valeur la plus courante, indépendamment des valeurs aberrantes. Le mode doit toujours être utilisé avec des données catégorielles, c'est-à-dire des données comportant des groupes distincts, puisque les groupes ne sont pas continus.

Bien qu'il soit plus facile d'utiliser le calculateur de moyenne arithmétique d'Omni, vous pouvez calculer le pourcentage moyen sur Excel :

1. Entrez les données souhaitées, par exemple dans les cellules A1 à A10.
2. Mettez toutes les cellules en surbrillance, faites un clic droit et sélectionnez « Formater les cellules ».
3. Dans la boîte de dialogue « Formater les cellules », cliquez sur « Nombre », sélectionnez « Pourcentages » dans la liste déroulante et indiquez le nombre de décimales souhaité.
4. Dans une autre cellule, entrez : =MOYENNE(cellule 1, cellule 2,….). Dans notre exemple, on écrirait =MOYENNE(A1:A10).
5. Voilà votre moyenne !

Oui, vous pouvez faire la moyenne des moyennes, mais cette méthode est souvent très imprécise et doit être utilisée avec précaution. Supposons que vous ayez deux pays, l'un avec une population de 10 millions d'habitants et un PIB de 30 000 €, l'autre avec une population de 10 000 habitants et un PIB de 2 000 €. Le PIB moyen par pays est de 16 000 € tandis que le PIB moyen par personne est d'environ 30 000 €, deux chiffres très différents montrant des choses très différentes. Donc, soyez prudent·e.

La question de savoir si vous devez utiliser la moyenne ou la médiane dépend des données que vous analysez. Si les données sont normalement distribuées et ne présentent pas de valeurs aberrantes, vous devriez probablement utiliser la moyenne, bien que la valeur soit assez similaire à celle de la médiane. Si les données sont fortement asymétriques, vous devriez utiliser la médiane, car elle est moins affectée par les valeurs aberrantes.

La moyenne des moyennes n'est pas toujours exacte. Elle peut être biaisée par deux facteurs principaux : les variables cachées et les moyennes pondérées. Les variables cachées sont des informations importantes qui ne sont pas prises en compte dans le calcul de la moyenne des moyennes. Cela peut entraîner une perte d'informations importantes. L'autre problème est de ne pas pondérer les moyennes lorsque c'est nécessaire. Si, par exemple, le nombre de visiteurs d'un site internet changeait chaque mois, alors le fait de ne pas pondérer en fonction du nombre de personnes entraînera forcément une perte d'informations.