Calcolatore per la Sezione Aurea

Il calcolatore per la sezione aurea calcolerà la lunghezza delle parti in cui devi dividere un segmento per ottenere la sezione aurea. Prima di passare al calcolo della sezione aurea, parliamo di cosa sia quest'ultimo. Di seguito troverai tutte le informazioni di cui hai bisogno!

Puoi anche dare un'occhiata al calcolatore di proporzioni 🇺🇸 se vuoi imparare qualcosa sui rapporti in generale.

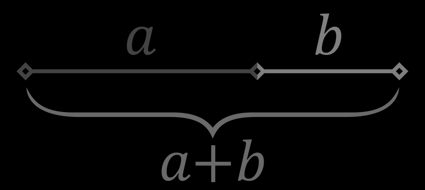
La sezione aurea (noto anche come rapporto aureo o proporzione aurea) si verifica quando un segmento viene diviso in due parti — la proporzione tra la parte più lunga e quella più corta deve essere uguale alla proporzione tra l'intero segmento e la parte più lunga. Cioè, se la parte più lunga ha lunghezza $a$ e la parte più corta ha lunghezza $b$, la formula della sezione aurea recita:

Per calcolare il valore della sezione aurea, devi risolvere l'equazione precedente per $a/b$. È conveniente riorganizzarla come:

Quindi, alla fine, dobbiamo solo risolvere $x$ nell'equazione quadratica $x^2-x-1=0$. Per farlo utilizziamo i metodi standard e scopriamo che il valore della sezione aurea è uguale a $\frac 12 (1+\sqrt{5})$, che è approssimativamente $1,\!61803\ 39887\ 5...$. Questo numero viene spesso indicato con la lettera greca $\phi$.

Ora sappiamo cos'è la sezione aurea e come calcolare il suo valore, quindi vediamo come verificare se due lunghezze date obbediscono a questa proporzione divina.

Ecco le istruzioni dettagliate per aiutarti a capire se due segmenti sono in rapporto aureo:

1. Trova la lunghezza del segmento più lungo ed etichettalo come a;
2. Trova la lunghezza del segmento più corto ed etichettalo come b;
3. Calcola a/b; e
4. Se la proporzione è (approssimativamente) uguale a 1,618, i segmenti sono in proporzione aurea.

Puoi anche utilizzare il calcolatore per la sezione aurea di Omni. Anche se qualsiasi calcolatore del rapporto 🇺🇸 può aiutarti, il nostro calcolatore per la sezione aurea si occupa nello specifico di questo problema, quindi non troverai uno strumento migliore di questo!

Il calcolatore per la sezione aurea di Omni non potrebbe essere più semplice e immediato. Ha tre campi, corrispondenti alle tre lunghezze che compaiono nella formula della proporzione aurea. Devi solo inserirne uno perché gli altri due vengano calcolati automaticamente. Non è fantastico?

Il rettangolo aureo è un rettangolo i cui lati rispettano la sezione aurea, cioè la proporzione tra lunghezza e larghezza è $1,\!618$. Questo rettangolo è spesso presente in arte, poiché si ritiene che sia il più gradevole all'occhio umano tra tutti i rettangoli. Il calcolatore per il rettangolo aureo è un modo comodo per trovare i lati di un rettangolo aureo invece di calcolarli a mano.

La sezione aurea ha sempre avuto una particolare rilevanza nella scienza e nell'arte grazie alle sue proprietà e al suo aspetto. Parlando di matematica:

• Un rettangolo aureo può essere diviso in due rettangoli aurei più piccoli (mantenendo le sue proporzioni); e
• La sezione aurea è profondamente correlata al numero 5. Questo numero compare nella sua definizione (φ = (1 + √5)/2) e nel pentagono come rapporto tra diagonale e lato.

In arte, la sezione aurea è apparso più recentemente — Salvador Dalí, ad esempio, ha utilizzato questo rapporto in molte delle sue opere.

Molte fonti storiche e contemporanee affermano che la sezione aurea è piuttosto onnipresente in natura. Alcuni esempi sono:

• Il modello di crescita delle foglie;
• Le superfici geometriche di alcune verdure e conchiglie; e
• Le proporzioni delle ossa di alcuni animali.

Tuttavia, se da un lato non possiamo negare la presenza di modelli geometrici in natura, dall'altro non possiamo confermare l'esattezza delle proporzioni degli esempi sopra citati — alcuni presentano variazioni enormi, mentre altri si avvicinano approssimativamente alla sezione aurea.