Euclidean Algorithm Calculator

With Omni's Euclidean algorithm calculator, you will learn an elegant and intriguing algorithm to find the greatest common divisor of any set of integer numbers. Keep reading this short article to learn:

• What is the Euclidean algorithm;
• What are the two types of Euclidean algorithms to calculate the GCD;
• Explanation step-by-step of the two algorithms;
• Expansion of the Euclidean algorithms to larger sets of numbers; and
• Some practical examples.

The Euclidean algorithm is an iterative process that allows you to calculate the greatest common divisor of a set of numbers without having to calculate the prime factorization, a process that can be long and highly demanding in resources.

The core concept of the Euclidean algorithm is to use the properties of the greatest common divisor to reduce the problem to a more manageable one.

We can identify two properties of the greatest common divisor that allow us to calculate the Euclidean algorithm for the GCD.

• The GCD of two numbers is also the GCD of their difference.
• The GCD of two numbers is also the GCD of the remainder of their quotient.

Using these two properties, we hope to reach a point where we can use two fundamental identities of the GCD:

• $\rm{GCD}(A,A) = A$; and
• $\rm{GCD}(0,A) = A$.

Let's see how we can translate the first property of the GCD into a working algorithm. We will start with two numbers.

We can weed out a special case from the beginning: if the two numbers are identical, then we already meet the first of the two identities: $\rm{GCD}(A,A) = A$.

If the numbers are different, we need to perform a few simple steps:

1. Subtract the smaller number from the larger one.
2. Substitute the larger number with the result of the previous step.

Before going on with the algorithm, let's wait and understand this step. We substituted the pair of numbers with an updated pair, but it maintains the same GCD. The Euclidean algorithm to calculate the GCD with subtraction is a simple repetition of the following steps:

3. Repeat steps 1. and 2. until the numbers in the pair are identical. The number appearing twice in the final pair is also the GCD of the original pair.

In the diagram below, you can see a graphical representation of the Euclidean algorithm for the greatest common divisor.

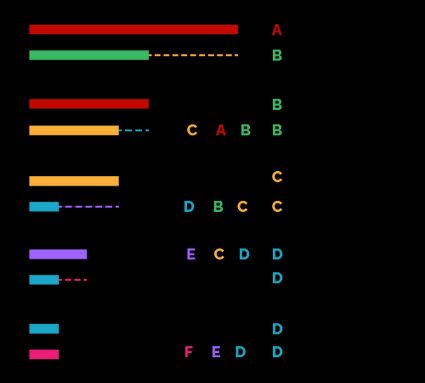
Let's check an example: we will use the numbers $364$ and $462$. Follow with using the Euclidean algorithm:

1. Subtract $364$ from $462$: $462-364=98$. Thanks to the properties of GCD, we can say that $\small \rm{GCD}(462,364)=\rm{GCD}(364,98)$.

2. After this substitution, we subtract the two numbers again: $364-98=266$. Now, we can say that $\small\rm{GCD}(364,98)=\rm{GCD}(266,98)$.

3. Repeat the subtraction: $266-98 = 168$, and since we can subtract $98$ again, we repeat the step: $168-98=70$. Now we can say: $\small\rm{GCD}(462,364) = {GCD}(266,98)$ $\small\rm = {GCD}(98,70)$.

4. Subtract $70$ from $98$: $98-70 = 28$. We're almost there: $\small\rm{GCD}(462,364)=\rm{GCD}(70,28)$.

5. Repeat: $70-28=42$, then $42-28=14$. The GCD of the original pair is equal to the GCD of the pair $(28,14)$.

6. We perform the last step: Subtract $24$ from $28$: $28-14=14$.

7. We found an identity of the GCD: $\small \rm GCD (462,364)= GCD (14,14)=14$.

We admit it; it was pretty long. Can we find a way to speed things up?

Let's use the second property of the GCD: the GCD of two numbers is also the GCD of the remainder of their quotient. In mathematical terms, we say:

Using this property, we describe another Euclidean algorithm for the GCD. Here are its steps for a generic pair of numbers $A$ and $B$, with $A>B$:

1. Calculate the remainder of the quotient between $A$ and $B$ with the operation $A\ \rm{mod}\ B$.
2. Substitute $A$ with the result of the previous step.
3. Repeat the steps above until the result of the modulo operation is $0$. At this step, the last non-zero number also corresponds to the GCD thanks to the second GCD identity: ${\rm GCD}(N,0) = N$.

Here you can see a graphical representation of this form of the Euclidean algorithm.

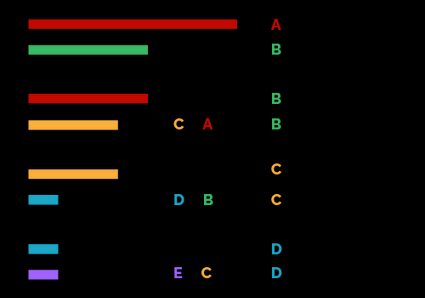
Let's see how to calculate the GCD with the Euclidean algorithm using the modulo operation with the same numbers as the previous example: $462$ and $364$.

1. The first step is to define this identity:

2. Repeat the modulo operation for the last pair of numbers, $364$ and $98$:

3. Rinse, and repeat!

4. We're almost there!

5. Now, you can almost see it: one last effort. Perform the modulo operation again:

Finally we can identify the second identity of the GCD:

And we can say that $\rm{GCD}(462,364)=\rm{GCD}(14,0)=14$.

Can we use the Euclidean algorithms to calculate the greatest common divisor of more than two numbers? The answer is yes! Simply create enough pairs to include all numbers at least once (this will be easy for even sets and slightly redundant for odd sets). If the result of the Euclidean algorithms applied to these sets is different, then rerun the algorithms on the results. Or use our Euclidean algorithm calculator for an easy and error-less answer!

Try our other tools related to the calculations of the GCD:

• GCF calculator;
• GCD calculator;
• Greatest common denominator calculator;
• Greatest common factor calculator; and
• Greatest common divisor calculator.

The steps of the Euclidean algorithm using subtraction are, for a pair of numbers A and B, with A > B:

1. Subtract the smaller number from the larger: C = A - B.

2. Substitute the larger number with the result: thanks to the properties of the GCD, GCD(A,B) = GCD(B,C).

3. Repeat the subtraction. If B > C, find D = B - C, and substitute: GCD(B,C) = GCD(C,D).

4. Repeat these steps until you reach a point where N = M - N.

5. Use this identity to find the GCD: GCD(A,B) = GCD(N,N) = N

Using the Euclidean algorithm with the remainder, we find the GCD of 336 and 176 in a few quick steps:

1. Use the following properties to reduce the numbers:

   GCD(336,176) = GCD(176,336 mod 176) = GCD(176,160)

2. Repeat the step for the new pair of numbers:

   GCD(176,160) = GCD(160,176 mod 160) = GCD(160,16)

3. In the last step, use the identity GCD(N,0) = N:

   GCD(160,16) = GCD(16,160 mod 16) = GCD(16,0) = 16

In most cases, using the Euclidean algorithm, either with subtraction (easier by hand) or the remainder (fastest but more complex), is a quick and safe way to calculate the GCD of two numbers. No guessing is involved (as in the prime factorization method), and it generally reaches a result in a reasonable number of operations.