Sector Area Calculator

With this sector area calculator, you'll quickly find any circle sector area, e.g., the area of a semicircle or quadrant. In this short article, we'll:

• provide a sector definition and explain what a sector of a circle is.
• show the sector area formula and explain how to derive the equation yourself without much effort.
• reveal some real-life examples where the sector area calculator may come in handy.

So let's start with the sector definition - what is a sector in geometry?

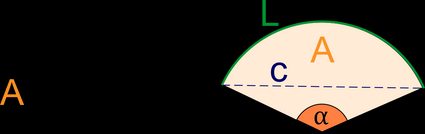
A sector is a geometric figure bounded by two radii and the included arc of a circle.

Sectors of a circle are most commonly visualized in pie charts, where a circle is divided into several sectors to show the weightage of each segment. The pictures below show a few examples of circle sectors - it doesn't necessarily mean that they will look like a pie slice, sometimes it looks like the rest of the pie after you've taken a slice:

You may, very rarely, hear about the sector of an ellipse, but the formulas are way, way more difficult to use than the circle sector area equations.

The formula for sector area is simple - multiply the central angle by the radius squared, and divide by 2:

• Sector Area = r² × α / 2

But where does it come from? You can find it by using proportions. All you need to remember is the circle area formula (and we bet you do!):

1. The area of a circle is calculated as A = πr². This is a great starting point.
2. The full angle is 2π in radians, or 360° in degrees, the latter of which is the more common angle unit.
3. Then, we want to calculate the area of a part of a circle, expressed by the central angle.

• For angles of 2π (full circle), the area is equal to πr²: 2π → πr²
• So, what's the area for the sector of a circle: α → Sector Area

4. From the proportion, we can easily find the final sector area formula:

Sector Area = α × πr² / 2π = α × r² / 2

The same method may be used to find arc length - all you need to remember is the formula for a circle's circumference. Read more about this in our circumference calculator and arc length calculator.

Finding the area of a semicircle or quadrant should be a piece of cake now, just think about what part of a circle they are!

1. Semicircle area: πr² / 2

• Knowing that it's half of the circle, divide the area by 2:

  Semicircle area = Circle area / 2 = πr² / 2

• Of course, you'll get the same result when using sector area formula. Just remember that straight angle is π (180°):

  Semicircle area = α × r² / 2 = πr² / 2

2. Quadrant area: πr² / 4

• As quadrant is a quarter of a circle, we can write the formula as:

  Quadrant area = Circle area / 4 = πr² / 4

• Quadrant's central angle is a right angle (π/2 or 90°), so you'll quickly come to the same equation:

  Quadrant area = α × r² / 2 = πr² / 4

We know, we know: "why do we need to learn that? We're never ever gonna use it". Well, we'd like to show you that geometry is all around us:

• If you're wondering how big cake you should order for your awesome birthday party - bingo, that's it! Use the sector area formula to estimate the size of a slice 🍰 for your guests so that nobody will starve to death.
• It's a similar story with pizza - have you noticed that every slice is a sector of a circle 🍕? For example, if you're not a big fan of the crust, you can calculate which pizza size will give you the best deal (don't forget about the tip afterwards).
• Any sewing enthusiasts here?👗 Sector area calculations may be useful in preparing a circle skirt (as it's not always a full circle but, you know, a sector of a circle instead).

Apart from those simple, real-life examples, the sector area formula may be handy in geometry, e.g., for finding the surface area of a cone.