Gear Ratio Speed Calculator

Q: How to calculate the gear ratio for gear speed?

When you have two connected gears, the gear ratio is the ratio between the output (driven) gear's number of teeth and the input (driving) gear's number of teeth . It allows the system designer to slow down or speed up a rotational speed, which has other useful effects like influencing the torque . The gear ratio is also the factor by which the required output speed is multiplied to determine the necessary input speed.

Q: What is the speed ratio for a gear ratio of 0.5?

The output gear's speed will be 0.5 times as slow (so 2 times as faster ) as the input's speed in a gear system with a total gear ratio of 0.5 .

Welcome to the gear ratio speed calculator! Here, we'll show you:

How to calculate the gear ratio and the speed at which your output gear rotates relative to your input gear; and
How to calculate speed from the gear ratio.

Ready to roll?

How do I use the gear ratio speed calculator?

The gear ratio speed calculator is easy to use and understand. Follow these simple steps:

Enter the number of teeth in each of your two gears. Make sure you know which is the driving gear and which one is driven!
Alternatively, to obtain the number of teeth for either gear for a suitable speed ratio, enter one gear's number of teeth and a suitable gear ratio instead.
Under the field for the gear ratio, we explain how the gear ratio influences the speed ratio between the input and output gears.
You can also enter an input speed to find the output speed corresponding to the two-gear system you've created above.

And that's it! You now know how to use the gear ratio speed calculator!

How to calculate the gear ratio for gear speed?

When you have two connected gears, the gear ratio is the ratio between the output (driven) gear's number of teeth and the input (driving) gear's number of teeth. It allows the system designer to slow down or speed up a rotational speed, which has other useful effects like influencing the torque. The gear ratio is also the factor by which the required output speed is multiplied to determine the necessary input speed.

So, if you want to know how to calculate the gear ratio and the speed ratio mathematically, the equation would be:

\footnotesize \text{Gear ratio} = \frac{ \text{\# teeth on output gear} }{ \text{\# teeth on input gear} }

For example, a two-gear system featuring an input gear with $10$ teeth and an output gear with $20$ teeth would have a gear ratio of $20/10 = 2$ , or $2:1$ . The input speed should be $2$ times faster than the target output speed.

Here, we express that the speed ratio (which has the same value as the gear ratio) is equal to the ratio of the input and output speed, as shown in this equation:

\footnotesize \text{Speed ratio} = \frac{ \text{input gear speed} }{ \text{output gear speed} }

The relationship between the gear ratio and the speed ratio

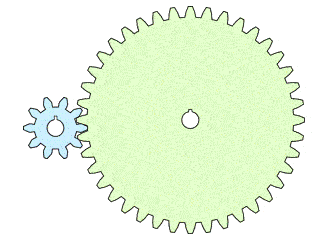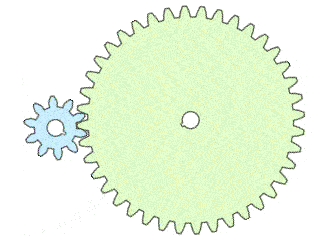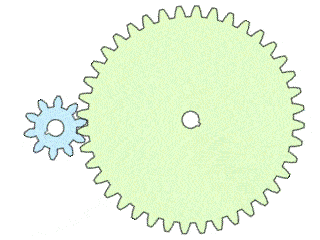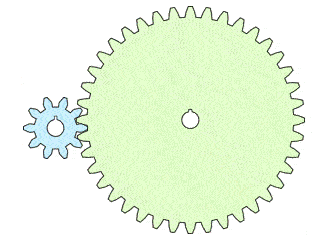
The speed ratio is all about angles. The input and output gears interlock, and so they each rotate one tooth at a time, together.

If the input gear has fewer teeth than the output gear, the input gear has a larger angle between teeth, resulting in a higher rotational speed on the input than the output. The speed ratio is then greater than 1.
If the input gear has more teeth than the output gear, the angle between the input's teeth is smaller, and the input gear rotates slower than the output. The gear speed ratio is less than 1.

See the animation below: Having more teeth on the output (right) gear means a smaller angle to turn per tooth compared to the input (left) gear. This results in a gear speed ratio of >1 and a faster rotational speed on the input compared to the output.

An animation of a gear train with an input gear spinning four times faster than its output gear.

FAQs

How do I calculate a vehicle's speed from its gear ratio?

To calculate the speed of the vehicle, follow these steps:

Determine the engine's speed in rotations per minute (rpm). Consult the car's tachometer for this value.
Multiply it with 3.6 × π × r, where r is the wheel radius in meters.
Divide it by 30 × g, where g is the gear ratio at the gearbox.
If the vehicle has a differential gear ratio, divide your result by it.

The result is the vehicle's speed in km/h.

How do I calculate the speed ratio of gears?

The speed ratio is equivalent to the normal gear ratio despite being calculated the opposite way. The gear ratio is the ratio of output teeth to input teeth (e.g., with 10 teeth on the input and 20 teeth on the output, the gear ratio is 20/10 or 2:1. The speed ratio is the ratio of input speed to output speed (e.g., with input and output rotational speeds of 30 rpm and 15 rpm, respectively, the speed ratio is 30/15 or 2:1).

What is the speed ratio for a gear ratio of 0.5?

The output gear's speed will be 0.5 times as slow (so 2 times as faster) as the input's speed in a gear system with a total gear ratio of 0.5.