Last updated: Jul 14, 2024

Wavenumber Calculator

Q: What is the SI unit of wavenumber?

The SI unit of wavenumber is m⁻¹ . We define wavenumber as the number of wavelengths per unit distance, i.e., wavenumber = 1/ wavelength . The SI unit of wavelength is meter or m. Hence the SI unit of wavenumber is m⁻¹.

New

Table of contents

What is wavenumber? - Wavenumber definition How to calculate wavenumber - Wavenumber formula How to use the wavenumber calculator Other wave calculators FAQs

Omni's wavenumber calculator allows you to calculate the wavenumber from wavelength and vice-versa.

Continue reading this article to learn what wavenumber is and how to calculate wavenumber from the wavelength or frequency and velocity of a wave.

Before understanding the wavenumber, let us first try to revise some basic concepts of wave motion.

What is wavenumber? - Wavenumber definition

We know that wave motion is a disturbance that travels from its point of origin. The physical characteristics required to describe a wave are its amplitude and wavelength (see figure 1).

The amplitude of a wave is the maximum distance from the equilibrium position, i.e., the distance between the central line and the peak of the crest or bottom of the trough. The wavelength of a wave is the length of one wave, i.e., the distance between two crests or two troughs.

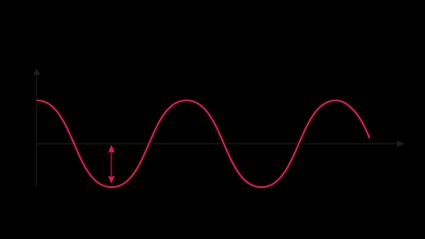
Physical characteristics describing a wave motion. — Fig 1: A wave can be described by physical characteristics like amplitude and wavelength.

In general, while describing wave motion in physics, we use the term angular wavenumber and represent it by the symbol $k$ . It is defined as the number of radians per unit distance. The SI unit of angular wavenumber is $\rm{radian/meter}$ or simply $\rm m^{-1}$ .

In spectroscopic studies and chemistry, the term wavenumber (or wave number) represents the number of wavelengths per unit length. The SI unit of wavenumber is $\rm m^{-1}$ .

How to calculate wavenumber - Wavenumber formula

The angular wavenumber ( $k$ ) is related to the wavelength ( $\lambda$ ) by the equation:

\quad \small \begin{align*} k &= \frac{2\pi}{\lambda}\\ \end{align*}

In spectroscopic studies, we calculate wavenumber using one of the following formulae:

\quad \small \begin{align*} \overline{\nu} &= \frac{1}{\lambda}\\ \\ or \quad \overline{\nu} &= \frac{f}{c}\\ \end{align*}

Where:
$\overline{\nu}$ - Wavenumber;
$\lambda$ - Wavelength;
$c$ - Speed of light in vacuum; and
$f$ - Frequency of the radiation.

How to use the wavenumber calculator

Now let us see how we can calculate the wavenumber for a light wave if its wavelength is 700 nm.

Enter the wavelength of the wave, i.e., $700\ \text{nm}$ .
The calculator will display the wavenumber ( $1,428,572\ \rm m^{-1}$ ) and angular wavenumber ( $8,975,979\ \text{radian/m}^{-1}$ )
You can also use this calculator in Wave velocity and frequency mode to calculate the wavenumber from the frequency and velocity of waves.

Other wave calculators

If you liked this tool, do check out our other calculators to determine the properties of waves:

FAQs

What is the SI unit of wavenumber?

The SI unit of wavenumber is m⁻¹. We define wavenumber as the number of wavelengths per unit distance, i.e., wavenumber = 1/ wavelength. The SI unit of wavelength is meter or m. Hence the SI unit of wavenumber is m⁻¹.

How do I calculate wavenumber and frequency of yellow radiation?

To calculate the wavenumber and frequency of yellow radiation (wavelength, λ = 5800 × 10⁻¹⁰ m), follow the given instructions:

Using the wavenumber formula, wavenumber = 1 / wavelength, determine the wavenumber as:
wavenumber = 1/(5800 × 10⁻¹⁰ m) = 1.724 × 10⁶ m⁻¹.
Using the formula, frequency = speed of light / wavelength, calculate the frequency as:
frequency = (3 × 10⁸ m/s) / (5800 × 10⁻¹⁰ m) = 5.172 × 10¹⁴ s⁻¹.