Omni Calculator logo
Ostatnia aktualizacja:

Kalkulator częstotliwości

Nowy

Spis treści

Definicja częstotliwości i wzór na częstotliwośćRównanie częstotliwości na podstawie długości faliJak korzystać z kalkulatora częstotliwości?Przykład: Jak obliczyć częstotliwość z okresu?Przykład: Jak znaleźć częstotliwość fali?Zastosowanie w praktyceFAQs

Kalkulator częstotliwości w mgnieniu oka pozwoli ci znaleźć częstotliwość fali, biorąc pod uwagę długość fali i jej prędkość lub okres. Prędkość fali możesz wybrać z listy predefiniowanych opcji — nie musisz znać wartości na pamięć!

W naszym tekście znajdziesz również definicję częstotliwości, dwa wzory na częstotliwość (przeliczające okres na częstotliwość oraz długość fali na częstotliwość) oraz kilka przykładów pokazujących, jak obliczyć częstotliwość różnych fal.

Jeśli chcesz dowiedzieć się więcej o falach, sprawdź kalkulator długości fali, a jeśli chcesz poznać częstotliwość tonów muzycznych, sprawdź kalkulator częstotliwości nut 🇺🇸.

Definicja częstotliwości i wzór na częstotliwość

Przyjrzyj się poniższemu modelowi fali; pomoże ci on zrozumieć pojęcia używane w definicji częstotliwości.

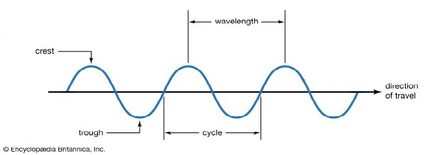
Obrazek fali wraz z terminologią.
Źródło: Encyklopedia Britannica

Częstotliwość to liczba zakończonych cykli fali na sekundę. Innymi słowy, częstotliwość mówi nam, ile grzbietów fali przechodzi przez dany punkt w ciągu sekundy.

Ta definicja częstotliwości prowadzi nas do najprostszego wzoru na częstotliwość:

f=1Tf=\frac{1}{T}

gdzie ff oznacza częstotliwość, a TT oznacza czas potrzebny do wykonania jednego cyklu fali mierzony w sekundach.

Jednostką częstotliwości w układzie SI jest herc (Hz), który jest równy 1/s (jeden cykl na sekundę). Inne jednostki częstotliwości to miliherc (mHz), kiloherc (kHz), megaherc (MHz), gigaherc (GHz) i teraherc (THz).

Równanie częstotliwości na podstawie długości fali

Spójrz na kolejny obrazek, który pozwoli nam dostrzec związek między częstotliwością a długością fali. Długość fali to odległość między dwoma sąsiednimi grzbietami (lub dolinami). Innymi słowy — jest to długość jednego cyklu fali. Im dłuższa jest fala, tym niższa jest częstotliwość:

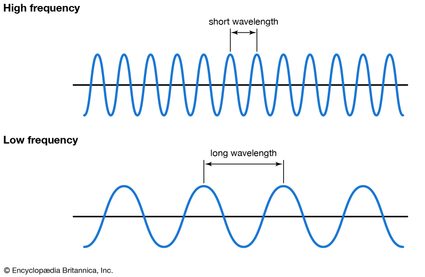
Rysunek fali o niskiej częstotliwości i wysokiej częstotliwości.
Źródło: Encyklopedia Britannica

Inny istotny fakt — to, z jaką prędkością poruszają się fale (prędkość fali) określa, ile z nich przejdzie przez dany punkt w ciągu sekundy. Oznacza to, że im większa prędkość fali, tym większa częstotliwość.

Te dwie zależności między częstotliwością a długością fali (λ\lambda) oraz między częstotliwością a prędkością (vv) sprowadzają nas do następującego równania częstotliwości:

f=vλf=\frac{v}{\lambda}

Jak korzystać z kalkulatora częstotliwości?

Nasz kalkulator częstotliwości uwzględnia wyżej opisane wzory na częstotliwość. Dlatego możesz go używać jako przelicznika okresu na częstotliwość lub kalkulatora częstotliwości, gdy masz podaną długość fali.

Jak używać go jako kalkulatora częstotliwości względem okresu? (Jak znaleźć częstotliwość, jeśli znasz okres?)

  1. Wprowadź czas, w którym występuje jeden cykl fali (okres). Kalkulator wyznaczy częstotliwość.

  2. Możesz też użyć tego kalkulatora do wyznaczenia okresu, jeśli znasz jego częstotliwość.

Jak użyć go jako kalkulatora częstotliwości, znając długość fali? (Jak obliczyć częstotliwość z długości fali?)

  1. Wpisz prędkość fali w drugie pole lub wybierz rodzaj fali i jej ośrodek z listy w pierwszym polu. Domyślne ustawienie to światło w próżni. Jeśli wybierzesz opcję „Wprowadź własną prędkość fali”, możesz wpisać dowolną prędkość fali wedle uznania.

  2. Wpisz długość fali, a pojawi się wartość częstotliwości.

Czyli w zasadzie można wpisać dwie dowolne zmienne, a trzecia pojawi się natychmiast 😀

Przykład: Jak obliczyć częstotliwość z okresu?

Aby rozwiać wszelkie wątpliwości dotyczące sposobu obliczania częstotliwości znając okres, przeanalizujmy kilka prostych przykładów. Po pierwsze, przypomnij sobie związek między częstotliwością a okresem:

f=1Tf=\frac{1}{T}

Przykład 1:

Jak znaleźć częstotliwość fali, w której jeden cykl zakończony jest w 0,25 s:

f=1T=10, ⁣25 s=4⋅1s\begin{align*} f&=\frac{1}{T}\\[1.2em] &=\frac{1}{0,\!25\ \text{s}}\\[1.2em] &= 4\cdot\frac{1}{\text{s}} \end{align*}

Pamiętaj, aby przeliczyć 1s\frac{1}{\text{s}} na jednostkę częstotliwości:

f=4 Hzf = 4\ \text{Hz}

Przykład 2:

Jak znaleźć częstotliwość fali, dla której w ciągu 1 minuty występuje 360 cykli:

f=3601 m=36060 s=6s=6 Hz\begin{align*} f&=\frac{360}{1\ \text{m}}\\[1.2em] &=\frac{360}{60\ \text{s}}\\[1.2em] &= \frac{6}{\text{s}}\\[1.2em] &= 6\ \text{Hz} \end{align*}

Przykład: Jak znaleźć częstotliwość fali?

Tym razem, chcemy się dowiedzieć jak znaleźć częstotliwość fali, jeśli mamy podaną jej prędkość i długość. Zastosuj następujący wzór na częstotliwość:

f=vλf=\frac{v}{\lambda}

Przykład 1:

Prędkość fali jest równa 320 m/s, a jej długość wynosi 8 m. Szukając jej częstotliwości, mamy:

f=vλ=320 ms8 m=40s=40 Hz\begin{align*} f&=\frac{v}{\lambda}\\[1.2em] &=\frac{320\ \tfrac{\text{m}}{\text{s}}}{8\ \text{m}}\\[1.2em] &= \frac{40}{\text{s}}\\[1.2em] &= 40\ \text{Hz} \end{align*}

Przykład 2:

Znajdź częstotliwość światła, jeśli długość fali jest równa 3000 km. Prędkość fali jest równa prędkości światła w próżni w przybliżeniu równej 300,000 kms300,\hspace{-0.05cm}000\ \tfrac{\text{km}}{\text{s}}. Korzystając ze wzoru na częstotliwość, otrzymujemy:

f=vλ≈300,000 kms3,000 km≈100s≈100 Hz\begin{align*} f&=\frac{v}{\lambda}\\[1.2em] &\approx\frac{300,\hspace{-0.05cm}000\ \tfrac{\text{km}}{\text{s}}}{3,\hspace{-0.05cm}000\ \text{km}}\\[1.2em] &\approx \frac{100}{\text{s}}\\[1.2em] &\approx 100\ \text{Hz} \end{align*}

Zastosowanie w praktyce

W komunikacji bezprzewodowej mamy do czynienia z obszarem wyznaczonym elipsoidą obrotową pomiędzy anteną nadawczą a anteną odbiorczą. Obszar ten jest zdeterminowany przez odległość między antenami i częstotliwość fali. Nazywa się on strefą Fresnela i wygląda w przybliżeniu w ten sposób:

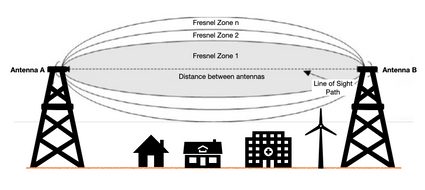
Strefa Fresnela.

Z głównego wzoru na strefę Fresnela wnioskujemy, że im wyższa częstotliwość, tym mniejsza objętość elipsoidy, która powinna pozostać pozbawiona przeszkód dla prawidłowej komunikacji bezprzewodowej. I odwrotnie — dla niskiej częstotliwości, otrzymujemy większą strefę Fresnela, którą budynki lub drzewa mogą łatwo zablokować i w ten sposób doprowadzić do zakłóceń w komunikacji bezprzewodowej.

💡 Możesz dowiedzieć się więcej o strefie Fresnela sprawdzając nasz kalkulator strefy Fresnela 🇺🇸.

Kiedy dwie fale o różnych częstotliwościach interferują ze sobą konstruktywnie i destruktywnie, wytwarzają wzór interakcji zwany dudnieniem. Możesz obliczyć konkretną częstotliwość dudnienia za pomocą kalkulatora częstotliwości dudnień 🇺🇸.

Innym interesującym zjawiskiem wynikającym z interakcji fal o różnych częstotliwościach jest rezonans. Rezonans może wystąpić na przykład, gdy powietrze przepływa przez wnękę, na przykład podczas dmuchania w szyjkę pustej butelki.

Taka wnęka rezonansowa jest znana jako rezonator Helmholtza. Jeśli objętość wnęki się zmienia, zmienia się częstotliwość rezonansowa. W kalkulatorze rezonatora Helmholtza 🇺🇸 możesz określić częstotliwość rezonansową wnęk o różnych objętościach.

FAQs

Jak obliczyć częstotliwość?

Musisz znać albo długość fali oraz prędkość, albo długość i okres fali (czas potrzebny na wykonanie jednego cyklu fali). Jeśli znasz okres:

  1. Przelicz go na sekundy i podziel 1 przez okres.
  2. Wynikiem będzie częstotliwość wyrażona w hercach.

Jeśli chcesz obliczyć częstotliwość z długości fali i prędkości fali:

  1. Upewnij się, że mają one tę samą jednostkę długości.
  2. Podziel prędkość fali przez długość fali.
  3. Przelicz wynik na herce. Wartość 1/s jest równoważna 1 hercowi.

Jak znaleźć długość fali z częstotliwości?

  1. Określ prędkość fali.
  2. Ustal, jaka jest jej częstotliwość.
  3. Zamień herce na 1/s.
  4. Upewnij się, że prędkość fali i częstotliwość mają tę samą jednostkę czasu.
  5. Podziel prędkość fali przez częstotliwość.

Jaki jest związek między częstotliwością a długością fali?

Częstotliwość jest równa prędkości fali podzielonej przez długość fali. Zatem im dłuższa fala, tym mniejsza częstotliwość, a im krótsza fala, tym większa częstotliwość. Innymi słowy, częstotliwość jest odwrotnie proporcjonalna do długości fali.

W czym mierzy się częstotliwość?

Częstotliwość fali mierzy się w hercach. 1 Herc jest równoważny 1/s — czyli jednemu cyklowi na sekundę. Pokrewne jednostki to miliherc (jedna tysięczna herca), kiloherc (tysiąc herców), megaherc (milion herców) i gigaherc (miliard herców). Nazwa jednostki pochodzi od nazwiska Heinricha Rudolfa Hertza, fizyka, który udowodnił istnienie fal elektromagnetycznych.

Jak znaleźć częstotliwość fali?

  1. Ustal prędkość fali.
  2. Określ długość fali.
  3. Upewnij się, że prędkość fali i długość fali mają tę samą jednostkę długości, np. jeśli prędkość jest wyrażona w metrach na sekundę, to długość fali powinna być określona w metrach.
  4. Podziel prędkość fali przez długość fali.
  5. Przelicz wynik na herce. Jeden herc równoważny jest 1/s — jednemu cyklowi na sekundę.

Jaką częstotliwość ma 5G?

5G, czyli standard technologiczny piątej generacji dla sieci komórkowych, działa na różnych pasmach częstotliwości, które dzielą się na dwa zakresy częstotliwości. Pierwszy zakres obejmuje częstotliwości od 450 MHz do 6 GHz, a drugi zakres częstotliwości odpowiada wartościom od 24,25 GHz do 52,6 GHz.

Który kolor światła ma najwyższą częstotliwość?

Fiolet to kolor o najwyższej częstotliwości, która mieści się w zakresie od około 670 do 750 teraherców. Po drugiej stronie spektrum znajduje się czerwień o częstotliwości między 430 a 480 teraherców.

Jaki jest związek między częstotliwością a energią?

Energia jest wprost proporcjonalna do częstotliwości. Innymi słowy, im wyższa częstotliwość, tym większa energia. Związek między częstotliwością a energią opisuje następujący wzór na energię fotonu:

E = h ∙ f

gdzie „E” to symbol energii, „h” to stała Plancka, a „f” oznacza częstotliwość.

Który rodzaj fal ma największą częstotliwość?

Promienie gamma to fale elektromagnetyczne o największej częstotliwości, czyli większej niż 1019 Hz. Mają one najwyższą energię i najkrótszą długość fali spośród wszystkich fal elektromagnetycznych. Ich wysoka energia umożliwia odrywanie elektronów od atomów i uszkadzanie żywych komórek. Źródłem promieniowania gamma są gwiazdy neutronowe, supernowe, wybuchy jądrowe i wyładowania atmosferyczne.

Jak wyznaczyć okres znając częstotliwość?

  1. Wzór na okres to T = 1 / f, gdzie „T” to okres — czas potrzebny na wykonanie jednego cyklu, a „f” to częstotliwość.
  2. Aby otrzymać okres z częstotliwości, po pierwsze przelicz częstotliwość z herców na 1/s. Jeden herc jest równoważny 1/s.
  3. Następnie podziel 1 przez częstotliwość. Wynikiem będzie czas (okres) wyrażony w sekundach.
Check out 22 similar rotational and periodic motion calculators 🌎
Angular accelerationAngular displacementAngular frequency...19 more