Kalkulator pierwiastka kwadratowego

Nasz kalkulator pierwiastka kwadratowego szacuje pierwiastek kwadratowy dowolnej liczby dodatniej. Po prostu wprowadź wybraną liczbę i odczytaj wyniki. Wszystko jest obliczane szybko i automatycznie! Dzięki temu narzędziu możesz również oszacować kwadrat wybranej liczby (wystarczy wpisać wartość w drugim polu), co może okazać się bardzo pomocne w znajdowaniu zmiennych idealnego równania kwadratowego.

Trudzisz się z podstawowymi operacjami arytmetycznymi: dodawaniem pierwiastków kwadratowych, odejmowaniem pierwiastków kwadratowych, mnożeniem pierwiastków kwadratowych lub dzieleniem pierwiastków kwadratowych? Już nie musisz! W poniższym tekście znajdziesz szczegółowe wyjaśnienie różnych własności pierwiastków kwadratowych, np. jak upraszczać pierwiastki kwadratowe, wraz z wieloma różnymi przykładami. Dzięki temu artykułowi nauczysz się raz na zawsze znajdować pierwiastki kwadratowe!

Czy zastanawiałeś się kiedyś, jakie jest pochodzenie symbolu pierwiastka kwadratowego √? Możemy Cię zapewnić, że ta historia nie jest tak prosta, jak mogłoby się wydawać. Pochodzenie symbolu pierwiastka sięga czasów starożytnych, podobnie jak pochodzenie procentu.

Jeśli szukasz wykresu pierwiastka kwadratowego lub właściwości funkcji pierwiastka kwadratowego, skieruj się bezpośrednio do odpowiedniej sekcji (wystarczy kliknąć powyższe linki!). Wyjaśniamy tam, czym jest pochodna pierwiastka kwadratowego, korzystając z podstawowej definicji pierwiastka kwadratowego; omawiamy również sposób obliczania pierwiastków kwadratowych z potęg lub pierwiastków kwadratowych z ułamków. Wreszcie, jeśli jesteś wystarczająco wytrwały/a, dowiesz się, że pierwiastek kwadratowy liczby ujemnej jest w rzeczywistości możliwy. W ten sposób wprowadzamy liczby zespolone, które znajdują szerokie zastosowanie w fizyce i matematyce.

Pierwiastki kwadratowe były znane już w starożytności. Najwcześniejsza gliniana tabliczka z poprawną wartością do 5 miejsc po przecinku √2 = 1,41421 pochodzi z Babilonii (1800 p.n.e. - 1600 p.n.e.). Wiele innych dokumentów wskazuje, że pierwiastki kwadratowe były również używane przez starożytnych Egipcjan, Hindusów, Greków i Chińczyków. Jednak pochodzenie symbolu pierwiastka √ jest nadal w dużej mierze spekulatywne.

• Wielu uczonych uważa, że pierwiastek kwadratowy wywodzi się od litery "r" - pierwszej litery łacińskiego słowa radix oznaczającego korzeń.
• Inna teoria głosi, że symbol pierwiastka kwadratowego został zaczerpnięty z arabskiej litery ج, która została umieszczona w oryginalnej formie ﺟ w słowie جذر - korzeń (język arabski jest pisany od prawej do lewej).

Pierwsze użycie symbolu pierwiastka kwadratowego √ nie zawierało poziomego "paska" nad liczbami wewnątrz symbolu pierwiastka kwadratowego √‾. "Pasek" jest znany jako vinculum w języku łacińskim, co oznacza wiązanie. Mimo, że symbol z vinculum jest obecnie w codziennym użyciu, zwykle pomijamy to podkreślenie w wielu tekstach, na przykład w artykułach w Internecie. Zapis wyższych stopni pierwiastka został zasugerowany przez Alberta Girarda, który umieścił indeks stopnia w otworze znaku rodnika, np. ³√ lub ⁴√.

W matematyce tradycyjnymi operacjami na liczbach są dodawanie, odejmowanie, mnożenie i dzielenie. Niemniej jednak czasami dodajemy do tej listy bardziej zaawansowane operacje i manipulacje: pierwiastki kwadratowe, potęgi, logarytmy, a nawet funkcje trygonometryczne (np. sinus i cosinus). W tym artykule skupimy się tylko na definicji pierwiastka kwadratowego.

Pierwiastek kwadratowy danej liczby x to każda liczba y, której kwadrat y² = y × y daje pierwotną liczbę x. Dlatego wzór na pierwiastek kwadratowy można wyrazić jako:

√x = y ⟺ x = y²,

gdzie ⟺ jest symbolem matematycznym, który oznacza jeśli i tylko jeśli. Każda dodatnia liczba rzeczywista zawsze ma dwa pierwiastki kwadratowe — pierwszy jest dodatni, a drugi ujemny. Jednakże, dla wielu praktycznych celów, zazwyczaj używamy pierwiastka dodatniego. Jedyną liczbą, która ma jeden pierwiatek kwadratowy jest zero. Dzieje się tak, ponieważ √0 = 0, a zero nie jest ani dodatnie, ani ujemne.

Istnieje również inna popularna notacja pierwiastków kwadratowych, która może być wygodniejsza w wielu złożonych obliczeniach. Ten alternatywny wzór na pierwiastek kwadratowy mówi, że pierwiastek kwadratowy liczby jest liczbą podniesioną do połowy wykładnika:

√x = x^(1/2) = x^0,5

W interpretacji geometrycznej pierwiastek kwadratowy danego pola kwadratu daje długość jego boku. Dlatego √ ma w nazwie słowo kwadrat. Podobna sytuacja ma miejsce w przypadku pierwiastka sześciennego, ∛. Jeśli weźmiesz pierwiastek sześcienny z objętości sześcianu, otrzymasz długość jego krawędzi. Podczas gdy pierwiastki kwadratowe są używane przy rozważaniu pól powierzchni, pierwiastki sześcienne są przydatne do określania ilości, które odnoszą się do objętości, np. gęstości.

Może nie jesteśmy zbyt skromni, ale uważamy, że najlepsza odpowiedź na pytanie jak znaleźć pierwiastek kwadratowy jest prosta: użyj kalkulatora pierwiastków kwadratowych! Możesz go używać zarówno na komputerze, jak i na smartfonie, aby szybko oszacować pierwiastek kwadratowy danej liczby. Niestety, czasami zdarzają się sytuacje, w których możesz polegać tylko na sobie. Co wtedy? Aby się na to przygotować, powinieneś zapamiętać kilka podstawowych pierwiastków kwadratowych:

• Pierwiastek kwadratowy z 1: √1 = 1, ponieważ 1 ⋅ 1 = 1;

• Pierwiastek kwadratowy z 4: √4 = 2, ponieważ 2 ⋅ 2 = 4;

• Pierwiastek kwadratowy z 9: √9 = 3, ponieważ 3 ⋅ 3 = 9;

• Pierwiastek kwadratowy z 16: √16 = 4, ponieważ 4 ⋅ 4 = 16;

• Pierwiastek kwadratowy z 25: √25 = 5, ponieważ 5 ⋅ 5 = 25;

• Pierwiastek kwadratowy z 36: √36 = 6, ponieważ 6 ⋅ 6 = 36;

• Pierwiastek kwadratowy z 49: √49 = 7, ponieważ 7 ⋅ 7 = 49;

• Pierwiastek kwadratowy z 64: √64 = 8, ponieważ 8 ⋅ 8 = 64;

• Pierwiastek kwadratowy z 81: √81 = 9, ponieważ 9 ⋅ 9 = 81;

• Pierwiastek kwadratowy z 100: √100 = 10, ponieważ 10 ⋅ 10 = 100;

• Pierwiastek kwadratowy z 121: √121 = 11, ponieważ 11 ⋅ 11 = 121; oraz

• Pierwiastek kwadratowy z 144: √144 = 12, ponieważ 12 ⋅ 12 = 144.

Powyższe liczby są najprostszymi pierwiastkami kwadratowymi, ponieważ za każdym razem otrzymasz liczbę całkowitą. Spróbuj je zapamiętać! Ale co możesz zrobić, gdy istnieje liczba, która nie ma tak ładnego pierwiastka kwadratowego? Istnieje wiele rozwiązań. Po pierwsze, możesz spróbować przewidzieć wynik metodą prób i błędów. Powiedzmy, że chcesz oszacować pierwiastek kwadratowy z liczby 52:

1. Wiesz, że √49 = 7 i √64 = 8, więc √52 powinien być pomiędzy 7 i 8.

2. Liczba 52 jest bliższa 49 (efektywnie bliższa 7), więc możesz spróbować założyć, że √52 wynosi 7,3.

3. Następnie podnosisz do kwadratu 7,3, otrzymując 7,3² = 53,29 (jak mówi wzór na pierwiastek kwadratowy), który jest wyższy niż 52. Musisz spróbować z mniejszą liczbą, powiedzmy 7,2.

4. Kwadrat 7,2 wynosi 51,84. Teraz masz mniejszą liczbę, ale znacznie bliższą 52. Jeśli ta dokładność cię satysfakcjonuje, możesz zakończyć szacowanie w tym miejscu. W przeciwnym razie możesz powtórzyć procedurę z liczbą wybraną między 7,2 a 7,3, np. 7,22 i tak dalej.

Innym podejściem jest uproszczenie najpierw pierwiastka kwadratowego, a następnie użycie przybliżeń pierwiastków kwadratowych liczb pierwszych (zwykle zaokrąglonych do dwóch miejsc po przecinku):

• Pierwiastek kwadratowy z 2: √2 ≈ 1,41,
• Pierwiastek kwadratowy z 3: √3 ≈ 1,73,
• Pierwiastek kwadratowy z 5: √5 ≈ 2,24,
• Pierwiastek kwadratowy z 7: √7 ≈ 2,65,
• Pierwiastek kwadratowy z 11: √11 ≈ 3,32,
• Pierwiastek kwadratowy z 13: √13 ≈ 3,61,
• Pierwiastek kwadratowy z 17: √17 ≈ 4,12,
• Pierwiastek kwadratowy z 19: √19 ≈ 4,34 itd.

Spróbujmy ponownie znaleźć pierwiastek kwadratowy z 52. Możesz uprościć go do √52 = 2√13 (dowiesz się, jak upraszczać pierwiastek kwadratowy w następnej sekcji), a następnie zastąpić √13 ≈ 3,61. Na koniec wykonaj mnożenie √52 ≈ 2 ⋅ 3,61 = 7,22. Wynik jest taki sam jak poprzednio!

W niektórych sytuacjach nie musisz znać dokładnego wyniku pierwiastka kwadratowego. Jeśli tak jest, nasz kalkulator pierwiastków kwadratowych jest najlepszą opcją do oszacowania wartości każdego pierwiastka kwadratowego, którego potrzebujesz. Na przykład, powiedzmy, że chcesz wiedzieć, czy 4√5 jest większe niż 9. Z kalkulatora wiesz, że √5 ≈ 2,23607, więc 4√5 ≈ 4 ⋅ 2,23607 = 8,94428. Jest ona bardzo bliska 9, ale nie jest od niej większa! Kalkulator pierwiastka kwadratowego podaje wartość końcową ze stosunkowo dużą dokładnością (do pięciu cyfr w powyższym przykładzie).

Pamiętaj, że nasz kalkulator automatycznie przelicza liczby wprowadzone do któregokolwiek z pól. Możesz znaleźć pierwiastek kwadratowy konkretnej liczby, wypełniając pierwsze okno lub otrzymując kwadrat liczby wprowadzonej w drugim oknie. Druga opcja jest przydatna w wyszukiwaniu idealnych kwadratów, które są niezbędne w wielu aspektach matematyki i nauk ścisłych. Na przykład, jeśli wpiszesz 17 w drugim polu, dowiesz się, że 289 jest kwadratem.

W niektórych zastosowaniach pierwiastka kwadratowego, szczególnie tych związanych z naukami ścisłymi, takimi jak chemia i fizyka, wyniki są preferowane w notacji naukowej. Krótko mówiąc, odpowiedź w notacji naukowej musi mieć kropkę dziesiętną między dwiema pierwszymi niezerowymi liczbami. Będzie ona reprezentowana jako liczba dziesiętna pomnożona przez 10 podniesiona do potęgi. Na przykład liczba 0,00345 jest zapisywana jako 3,45 ⋅ 10-³ w notacji naukowej, podczas gdy 145,67 jest zapisywane jako 1,4567 ⋅ 10² w notacji naukowej. Wyniki uzyskane za pomocą kalkulatora pierwiastków kwadratowych można przekonwertować na notację naukową za pomocą kalkulatora notacji naukowej.

Najpierw zastanówmy się, które pierwiastki kwadratowe można uprościć. Aby odpowiedzieć na to pytanie, musisz wziąć liczbę, która znajduje się po symbolu pierwiastka kwadratowego i znaleźć jej czynniki. Jeśli którykolwiek z jej czynników jest liczbą kwadratową (4, 9, 16, 25, 36, 49, 64 i tak dalej), to możesz uprościć pierwiastek kwadratowy. Dlaczego te liczby są podnoszone do kwadratu? Można je odpowiednio wyrazić jako 2², 3², 4², 5², 6², 7² itd. Zgodnie z definicją pierwiastka kwadratowego, możesz nazwać je idealnymi kwadratami. Spójrzmy na kilka przykładów:

• Czy potrafisz uprościć √27? Czynniki liczby 27 to 1, 3, 9, 27. Tutaj jest 9! Oznacza to, że możesz uprościć √27.

• Czy możesz uprościć √15? Czynniki liczby 15 to 1, 3, 5 i 15. W tych liczbach nie ma idealnych kwadratów, więc tego pierwiastka kwadratowego nie można uprościć.

Jak więc upraszczać pierwiastki kwadratowe? Aby to wyjaśnić, użyjemy poręcznej własności pierwiastka kwadratowego, o której mówiliśmy wcześniej, a mianowicie alternatywnego wzoru na pierwiastek kwadratowy:

√x = x^(1/2)

Możemy używać tych dwóch form pierwiastków kwadratowych i przełączać się między nimi, kiedy tylko chcemy. W szczególności pamiętaj, że potęga mnożenia dwóch konkretnych liczb jest równoważna mnożeniu tych konkretnych liczb podniesionych do tych samych potęg. Dlatego możemy napisać:

(x × y)^(1/2) = x^(1/2) ⋅ y^(1/2) ⟺ √(x × y) = √x × √y,

Jak możesz wykorzystać tę wiedzę? Argument pierwiastka kwadratowego zwykle nie jest idealnym kwadratem, który możesz łatwo obliczyć, ale może zawierać idealny kwadrat wśród swoich czynników. Innymi słowy, możesz zapisać go jako mnożenie dwóch liczb, gdzie jedna z liczb jest pierwiastkiem doskonałym, np. 45 = 9 ⋅ 5 (9 jest pierwiastkiem doskonałym). Wymóg posiadania co najmniej jednego czynnika, który jest pierwiastkiem doskonałym, jest niezbędny do uproszczenia pierwiastka kwadratowego. W tym momencie powinieneś już wiedzieć, jaki będzie następny krok. Musisz podstawić to mnożenie pod pierwiastek kwadratowy. W naszym przykładzie:

√45 = 45^(1/2) = (9 × 5)^(1/2) = 9^(1/2) ⋅ 5^(1/2) = √9 ⋅ √5 = 3√5.

Pomyślnie uprościłeś swój pierwszy pierwiastek kwadratowy! Oczywiście nie musisz zapisywać wszystkich tych obliczeń. Jeśli tylko pamiętasz, że pierwiastek kwadratowy jest równy połowie potęgi, możesz je skrócić. Poćwiczmy upraszczanie pierwiastków kwadratowych na innych przykładach:

• Jak uprościć pierwiastek kwadratowy z 27?

  √27 = √(9 ⋅ 3) = √9 ⋅ √3 = 3√3

• Jak uprościć pierwiastek kwadratowy z 8?

  √8 = √(4 ⋅ 2) = √4 ⋅ √2 = 2√2

• Jak uprościć pierwiastek kwadratowy liczby 144?

  √144 = √(4 ⋅ 36) = √4 ⋅ √36 = 2 ⋅ 6 = 12

W ostatnim przykładzie nie musiałeś w ogóle upraszczać pierwiastka kwadratowego, ponieważ liczba 144 jest kwadratem doskonałym. Możesz po prostu zapamiętać, że 12 ⋅ 12 = 144. Chcieliśmy jednak pokazać ci, że dzięki procesowi upraszczania możesz łatwo obliczać pierwiastki kwadratowe. Jest to przydatne, gdy masz do czynienia z dużymi liczbami.

Na koniec możesz zapytać, jak uprościć pierwiastki wyższych rzędów, np. pierwiastki sześcienne 🇺🇸. W rzeczywistości proces jest bardzo analogiczny do pierwiastków kwadratowych, ale w przypadku pierwiastków sześciennych musisz znaleźć co najmniej jeden czynnik, który jest wielokrotnością, tj. 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ i tak dalej. Następnie dzielisz swoją liczbę na dwie części i podstawiasz je pod pierwiastek sześcienny. Weźmy następujący przykład uproszczenia liczby ³√192:

∛192 = ∛(64 ⋅ 3) = ∛64 ⋅ ∛3 = 4∛3

Na pierwszy rzut oka może się to wydawać nieco skomplikowane, ale po kilku ćwiczeniach będziesz w stanie uprościć pierwiastki w swojej głowie. Zaufaj nam!

Dodawanie pierwiastków kwadratowych i odejmowanie pierwiastków kwadratowych

Niestety, dodawanie i odejmowanie pierwiastków kwadratowych nie jest tak proste, jak dodawanie i odejmowanie zwykłych liczb. Na przykład, jeśli 2 + 3 = 5, nie oznacza to, że √2 + √3 równa się √5. Aby zrozumieć, dlaczego tak jest, wyobraź sobie, że masz dwa różne typy kształtów: trójkąty 🔺 i okręgi 🔵. Co się stanie, gdy dodasz jeden trójkąt do jednego okręgu 🔺 + 🔵? Nic! Nadal masz jeden trójkąt i jeden okrąg 🔺 + 🔵. Z drugiej strony, co się stanie, gdy spróbujesz dodać trzy trójkąty do pięciu trójkątów: 3🔺 + 5🔺? Otrzymasz osiem trójkątów 8🔺.

Dodawanie pierwiastków kwadratowych jest bardzo podobne. Wynikiem dodawania √2 + √3 jest nadal √2 + √3. Nie możesz tego dalej upraszczać. Inaczej jednak wygląda sytuacja, gdy oba pierwiastki kwadratowe mają tę samą liczbę pod symbolem pierwiastka. Wtedy możemy je dodać tak jak zwykłe liczby (lub trójkąty). Na przykład, 3√2 + 5√2 równa się 8√2. To samo dotyczy odejmowania pierwiastków kwadratowych. Spójrzmy na więcej przykładów ilustrujących tę własność pierwiastków kwadratowych:

• Ile wynosi 6√17 + 5√17? Odpowiedź: 6√17 + 5√17 = 11√17;

• Ile to jest 4√7 - 7√7? Odpowiedź: 4√7 - 7√7 = -3√7;

• Ile to jest 2√2 + 3√8? Odpowiedź: 2√2 + 3√8 = 2√2 + 6√2 = 8√2, bo uprościliśmy √8 = √(4 ⋅ 2) = √4 ⋅ √2 = 2√2;

• Ile wynosi √45 - √20? Odpowiedź: √45 - √20 = 3√5 - 2√5 = √5, bo uprościliśmy √45 = √(9 ⋅ 5) = √9 ⋅ √5 = 3√5 oraz √20 = √(4 ⋅ 5) = √4 ⋅ √5 = 2√5;

• Ile wynosi 7√13 + 2√22? Odpowiedź: 7√13 + 2√22, nie możemy tego dalej upraszczać;

• Ile wynosi √3 - √18? Odpowiedź: √3 - √18 = √3 - 3√2, nie możemy tego dalej uprościć, ale przynajmniej uprościliśmy √18 = √(9 ⋅ 2) = √9 ⋅ √2 = 3√2.

Mnożenie pierwiastków kwadratowych i dzielenie pierwiastków kwadratowych

Skoro dodawanie pierwiastków kwadratowych to dla ciebie bułka z masłem, pójdźmy o krok dalej. Co powiesz na mnożenie pierwiastków kwadratowych i dzielenie pierwiastków kwadratowych? Nie bój się! W rzeczywistości już to zrobiłeś/aś podczas lekcji na temat upraszczania pierwiastków kwadratowych. Mnożenie pierwiastków kwadratowych opiera się na własności pierwiastka kwadratowego, z której korzystaliśmy już kilka razy, czyli:

√x = x^(1/2)

Czy pamiętasz jak mnożyć liczby podniesione do tej samej potęgi? Dla przypomnienia:

xⁿ ⋅ yⁿ = (x ⋅ y)ⁿ,

a zatem

x^(1/2) ⋅ y^(1/2) = (x ⋅ y)^(1/2) ⟺ √x ⋅ √y = √(x ⋅ y).

W przeciwieństwie do dodawania możesz pomnożyć każde dwa pierwiastki kwadratowe. Pamiętaj, że mnożenie jest przemienne, co oznacza, że kolejność mnożenia dwóch liczb nie ma znaczenia. Kilka przykładów powinno wyjaśnić tę kwestię:

• Ile to jest √3 ⋅ √2? Odpowiedź: √3 ⋅ √2 = √6;

• Ile to jest 2√5 ⋅ 5√3? Odpowiedź: 2√5 ⋅ 5√3 = 2 ⋅ 5 ⋅ √5 ⋅ √3 = 10√15, ponieważ mnożenie jest przemienne;

• Ile wynosi 2√6 ⋅ 3√3? Odpowiedź: 2√6 ⋅ 3√3 = 2 ⋅ 3 × √6 ⋅ √3 = 6√18 = 18√2, uprościliśmy √18 = √(9 ⋅ 2) = √9 ⋅ √2 = 3√2.

Dzielenie pierwiastka kwadratowego jest prawie takie samo, ponieważ:

x^(1/2) / y^(1/2) = (x / y)^(1/2) ⟺ √x / √y = √(x / y).

Wszystko, co musisz zrobić, to zastąpić znak mnożenia dzieleniem. Jednak podział nie jest operatorem komutatywnym! Musisz osobno obliczyć liczby stojące przed pierwiastkami kwadratowymi i liczby pod pierwiastkami kwadratowymi. Jak zawsze, poniżej znajdziesz kilka praktycznych przykładów:

• Ile wynosi √15 / √3? Odpowiedź: √15 / √3 = √5;

• Ile wynosi 10√6 / 5√2? Odpowiedź: 10√6 / 5√2 = (10 / 5) ⋅ (√6 / √2) = 2√3;

• Ile wynosi 6√2 / 3√5? Odpowiedź: 6√2 / 3√5 = (6 / 3) ⋅ (√2 / √5) = 2√(2/5) = 2√(0,4), zamieniliśmy tam ułamek zwykły 2/5 na ułamek dziesiętny 2/5 = 4/10 = 0,4.

Obliczanie pierwiastka kwadratowego z liczb podniesionych do potęgi lub pierwiastka kwadratowego z ułamków może nie być dla ciebie oczywiste. Ale z wiedzą, którą zdobyłeś/aś w poprzedniej sekcji, powinno to być łątwiejsze niż się wydaje! Zacznijmy od pierwiastków kwadratowych potęg. W tym przypadku łatwiej będzie ci skorzystać z alternatywnej postaci pierwiastka kwadratowego √x = x^(1/2). Czy pamiętasz zasadę potęgowania? Jeśli nie, oto krótkie przypomnienie:

(xⁿ)^m = x^{(n ⋅ m)}

gdzie n i m są dowolnymi liczbami rzeczywistymi. Teraz gdy umieścisz 1/2 zamiast m, otrzymasz nic innego jak ułamek jako wykładnik:

√(xⁿ) = (xⁿ)^(1/2) = x^(n/2)

W ten sposób znajdziesz pierwiastek kwadratowy liczby podniesionej do potęgi. Mówiąc o potęgach, powyższe równanie wygląda bardzo podobnie do standardowej funkcji gęstości rozkładu normalnego, która jest szeroko stosowana w statystyce.

Jeśli nadal nie masz pewności co do pierwiastków kwadratowych z potęg, oto kilka przykładów:

• Pierwiastek kwadratowy z 2⁴:

  √(2⁴) = (2⁴)^(1/2) = 2^(4/2) = 2² = 4

• Pierwiastek kwadratowy z 5³:

  √(5³) = (5³)^(1/2) = 5^(3/2)

• Pierwiastek kwadratowy z 4⁵:

  √(4⁵) = (4⁵)^(1/2) = 4^(5/2) = (2²)^(5/2) = 2⁵ = 32

Jak widzisz, czasami niemożliwe jest uzyskanie ładnego wyniku, jak w pierwszym przykładzie. Jednak w trzecim przykładzie pokazaliśmy ci małą sztuczkę z wyrażeniem 4 jako 2². Takie podejście może często uprościć bardziej skomplikowane równania.

A co z pierwiastkami kwadratowymi ułamków? Zajrzyj do poprzedniej sekcji, w której pisaliśmy o dzieleniu pierwiastków kwadratowych. Znajdziesz tam następującą zależność, która powinna wszystko wyjaśnić:

(x / y)^(1/2) ⟺ √x / √y = √(x / y)

gdzie x / y jest ułamkiem. Poniżej znajdziesz kilka przykładów pierwiatków kwadratowych ułamka:

• Pierwiastek kwadratowy z 4/9:

  √(4/9) = √4 / √9 = 2/3

• Pierwiastek kwadratowy z 1/100:

  √(1/100) = √1 / √100 = 1/10

• Pierwiastek kwadratowy z 1/5:

  √(1/5) = √1 / √5 = 1/√5 = √5/5

Pozostawianie pierwiastków w mianowniku nie jest dobrym nawykiem. Dlatego pozbyliśmy się go w ostatnim przykładzie. Po prostu pomnożyliśmy zarówno licznik, jak i mianownik przez tę samą liczbę (zawsze możemy to zrobić, ponieważ liczba, przez którą mnożymy, jest równa 1), w tym przypadku przez √5.

Funkcje odgrywają istotną rolę nie tylko w matematyce, ale także na wielu innych polach, takich jak fizyka, statystyka czy finanse. Funkcja f(x) to nic innego jak wzór, który mówi, jak wartość f(x) zmienia się wraz z argumentem x. Znajdziesz tam kilka funkcji, które możesz zastosować w prawdziwym życiu. Są one bardzo pomocne, jeśli chcesz wiedzieć, jak obliczyć procent składany lub oszacować przyszłą wartość renty.

Poniżej znajdziesz wykres pierwiastka kwadratowego, składającego się z połowy paraboli. Sprawdź go i spróbuj potwierdzić, na przykład, czy funkcja pierwiastka kwadratowego dla x = 9 wynosi 3, a dla x = 16 wynosi 4 (tak jak powinno być).

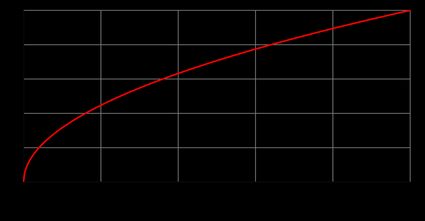
Wróćmy do funkcji pierwiastka kwadratowego f(x) = √x i zbadajmy, jakie są jej podstawowe właściwości. Rozważamy tutaj tylko dodatnią część f(x) (jak możesz zobaczyć na wykresie pierwiastka kwadratowego powyżej). Tak więc, funkcja pierwiastka kwadratowego:

• Jest ciągła i rosnąca dla wszystkich nieujemnych x;

• Jest różniczkowalna dla wszystkich dodatnich x (zobacz sekcję pochodna pierwiastka kwadratowego, aby uzyskać więcej informacji);

• Dochodzi do granicy nieskończoności, gdy x zbliża się do nieskończoności (lim √x → ∞, gdy x → ∞); i

• Jest liczbą rzeczywistą dla wszystkich nieujemnych x i liczbą zespoloną dla wszystkich ujemnych x.

Pochodna funkcji mówi nam, jak szybko ta funkcja zmienia się wraz z jej argumentem. Jednym z najprostszych przykładów w fizyce jest pozycja obiektu i jego prędkość (tempo zmiany pozycji). Powiedzmy, że funkcja x(t) opisuje, jak odległość poruszającego się samochodu od określonego punktu zmienia się w czasie t. Czy wiesz, co określa szybkość zmiany przebytej odległości? Odpowiedzią jest prędkość samochodu! Pochodną położenia x(t) jest więc prędkość v(t) (prędkość też może zależeć od czasu). Aby oznaczyć pochodną, zwykle używamy apostrofu v(t) = x'(t) lub symbolu pochodnej v(t) = dx(t)/dt.

Pochodna ogólnej funkcji f(x) nie zawsze jest łatwa do obliczenia. Jednak w pewnych okolicznościach, jeśli funkcja przyjmuje określoną postać, mamy pewne wzory. Na przykład, jeśli

f(x) = xⁿ,

gdzie n jest dowolną liczbą rzeczywistą, pochodne mają następującą postać:

f'(x) = n ⋅ x^(n-1).

Może na to nie wygląda, ale to odpowiada na pytanie jaka jest pochodna pierwiastka kwadratowego. Pamiętasz alternatywną (wykładniczą) postać pierwiastka kwadratowego? Pozwól, że ci przypomnimy:

√x = x^(1/2).

Widzisz, że w tym przypadku n = 1/2, więc pochodna pierwiastka kwadratowego wynosi:

(√x)' = (x^(1/2))' = 1/2 × x^(-1/2) = 1/(2√x).

Ponieważ liczba do potęgi ujemnej jest jedynką nad tą liczbą, oszacowanie pochodnej będzie obejmowało ułamki. Mamy narzędzie, które może być niezbędne podczas dodawania lub odejmowania ułamków o różnych mianownikach. Nazywa się ono kalkulator NWW 🇺🇸 i pozwala znaleźć najmniejszą wspólną wielokrotność.

Pochodna pierwiastka kwadratowego jest potrzebna do uzyskania współczynników w tak zwanym rozszerzeniu Taylora. Nie chcemy zbytnio zagłębiać się w szczegóły, więc krótko, seria Taylora pozwala przybliżyć różne funkcje za pomocą wielomianów, które są znacznie łatwiejsze do obliczenia. Na przykład, rozwinięcie Taylora √(1 + x) wokół punktu x = 0 jest dane przez:

√(1 + x) = 1 + 1/2 ⋅ x - 1/8 ⋅ x² + 1/16 ⋅ x³ - 5/128 ⋅ x⁴ + ...,

które jest ważne dla -1 ≤ x ≤ 1. Chociaż powyższe wyrażenie ma nieskończoną liczbę wyrazów, aby uzyskać przybliżoną wartość, możesz użyć tylko kilku pierwszych wyrazów. Spróbujmy! Z x = 0,5 i pierwszymi pięcioma wyrazami, otrzymasz:

√(1,5) = 1 + 1/2 ⋅ 0,5 - 1/8 ⋅ 0,25 + 1/16 ⋅ 0,125 - 5/128 ⋅ 0,0625,

√(1,5) ≈ 1,2241,

a rzeczywista wartość podana przez nasz kalkulator to √(1,5) ≈ 1,2247. Wystarczająco blisko!

To było dużo matematyki i równań do tej pory. Dla tych z was, którzy są wystarczająco wytrwali, przygotowaliśmy następną sekcję, która wyjaśnia, jak obliczać pierwiastek kwadratowy liczby ujemnej.

W szkole prawdopodobnie uczono cię, że pierwiastek kwadratowy liczby ujemnej nie istnieje. Jest to prawdą, gdy bierzesz pod uwagę tylko liczby rzeczywiste. Dawno temu, aby wykonywać zaawansowane obliczenia, matematycy musieli wprowadzić bardziej ogólny zbiór liczb — liczby zespolone. Można je wyrazić w następującej formie:

x = a + b ⋅ i,

gdzie x jest liczbą zespoloną z częścią rzeczywistą a i częścią urojoną b. Tym, co odróżnia liczbę zespoloną od rzeczywistej, jest liczba urojona i. Poniżej znajdziesz kilka przykładów liczb zespolonych: 2 + 3i, 5i, 1,5 + 4i oraz 2. Możesz być zaskoczony widząc 2, która jest liczbą rzeczywistą. Tak, ale jest to również liczba zespolona z b = 0. Liczby zespolone są uogólnieniem liczb rzeczywistych.

Póki co, liczba urojona i jest dla ciebie zapewne wciąż zagadką. Czym ona w ogóle jest? Cóż, choć może wyglądać dziwnie, jest zdefiniowana przez następujące równanie:

i = √(-1),

i to wszystko, czego potrzebujesz do obliczenia pierwiastka kwadratowego każdej liczby, niezależnie od tego, czy jest ona dodatnia, czy nie. Zobaczmy kilka przykładów:

• Pierwiastek kwadratowy z -9: √(-9) = √(-1 × 9) = √(-1)√9 = 3i;
• Pierwiastek kwadratowy z -13: √(-13) = √(-1 × 13) = √(-1)√13 = i√13; oraz
• Pierwiastek kwadratowy z -49: √(-49) = √(-1 × 49) = √(-1)√49 = 7i.

Prawda, że to proste? Ten problem nie pojawia się w przypadku pierwiastka sześciennego, ponieważ możesz uzyskać liczbę ujemną, mnożąc trzy identyczne liczby ujemne (czego nie możesz zrobić z dwiema liczbami ujemnymi). Na przykład:

³√(-64) = ³√[(-4)⋅(-4)⋅(-4)] = -4.

I to wszystko, co musisz wiedzieć o pierwiastkach kwadratowych!