Kalkulator odległości

Czy kiedykolwiek przyszło ci obliczyć odległość od jednego punktu do drugiego lub odległość między miastami? Czy na pewno wiesz, jaka jest definicja odległości? W Omni kalkulatorze odległości podamy wszystkie te odpowiedzi, a nawet więcej, w tym szczegółowe wyjaśnienie, jak obliczyć odległość między dowolnymi dwoma obiektami w przestrzeni 2D. Jako bonus, mamy fascynujący temat o tym, jak postrzegamy odległości (na przykład jako różnicę procentową); jesteśmy pewni, że ci się spodoba!

Wolisz oglądać niż czytać? Dowiedz się wszystkiego w 90 sekund dzięki poniższemu filmowi, który stworzyliśmy dla ciebie:

Zanim przejdziemy do obliczania odległości, powinniśmy wyjaśnić, czym ona właściwie jest. Najbardziej powszechnym znaczeniem jest jednowymiarowy dystans pomiędzy dwoma punktami. Ta definicja jest jednym ze sposobów na określenie tego, co prawie wszyscy intuicyjnie myślimy o odległości, ale nie jest to jedyna możliwość, w jaki sposób możemy mówić o odległości. W kolejnych rozdziałach zobaczymy, jak pojęcie odległości może oznaczać coś więcej niż długość, co jest przełomem w teorii względności Einsteina.

Jeśli będziemy trzymać się geometrycznej definicji odległości, nadal musimy zdefiniować, w jakiej przestrzeni pracujemy. W większości przypadków prawdopodobnie mówimy o trzech lub mniej wymiarach, ponieważ z tyloma zazwyczaj spotykamy się w życiu codziennym. W naszym kalkulatorze skupiamy się tylko na odległości 2D (z 1D jako szczególnym przypadkiem). Jeśli szukasz odległości 3D między dwoma punktami, zachęcamy do skorzystania z naszego kalkulatora odległości trójwymiarowej 🇺🇸 stworzonego specjalnie w tym celu.

Aby znaleźć odległość między dwoma punktami, pierwszą rzeczą, której potrzebujesz, są oczywiście dwa punkty. Punkty te są opisane przez ich współrzędne w przestrzeni. Dla każdego punktu w przestrzeni dwuwymiarowej potrzebujemy dwóch współrzędnych, które są unikalne dla tego punktu. Jeśli chcesz znaleźć odległość między dwoma punktami w przestrzeni 1D, nadal możesz użyć tego kalkulatora, po prostu ustawiając jedną ze współrzędnych tak, aby była taka sama dla obu punktów. Ponieważ jest to bardzo szczególny przypadek, od teraz będziemy mówić tylko o odległości w dwóch wymiarach.

Jeśli chcemy być matematycznie dokładni i precyzyjni, to następnym krokiem jest zdefiniowanie rodzaju przestrzeni, w której pracujemy. Nie, czekaj, nie uciekaj! To łatwiejsze niż myślisz. Jeśli nie wiesz, w jakiej przestrzeni pracujesz lub nawet nie wiedziałeś, że istnieje więcej niż jeden typ przestrzeni, najprawdopodobniej masz do czynienia z przestrzenią euklidesową. Ponieważ jest to „domyślna” przestrzeń, w której wykonujemy prawie każdą operację geometryczną, dlatego też ustawiliśmy ją dla kalkulatora odległości. Przyjrzyjmy się bliżej przestrzeni euklidesowej; co to jest, jakie ma właściwości i dlaczego jest tak ważna?

Przestrzeń euklidesowa lub geometria euklidesowa jest tym, co wszyscy zwykle myślimy o przestrzeni 2D, zanim zaczniemy studiować bardziej skomplikowane działy matematyki. W przestrzeni euklidesowej suma kątów trójkąta wynosi 180º, a kwadraty mają wszystkie kąty równe 90º; tak dzieje się zawsze. Jest to coś, co wszyscy przyjmujemy za pewnik, ale nie jest to prawdą we wszystkich przestrzeniach. Nie mylmy również przestrzeni euklidesowej z przestrzeniami wielowymiarowymi. Przestrzeń euklidesowa może mieć dowolną liczbę wymiarów, o ile jest ich skończona liczba i nadal są one zgodne z zasadami euklidesowymi.

Nie chcemy zanudzać cię matematycznymi definicjami tego, czym jest przestrzeń i co sprawia, że przestrzeń euklidesowa jest wyjątkowa, ponieważ byłoby to zbyt skomplikowane, aby wyjaśnić to w prostym kalkulatorze odległości. Możemy jednak spróbować podać kilka przykładów innych przestrzeni, które są powszechnie używane i które mogą pomóc zrozumieć, dlaczego przestrzeń euklidesowa nie jest jedyną przestrzenią. Ponadto mamy nadzieję, że zrozumiesz, dlaczego nie będziemy zawracać sobie głowy obliczaniem odległości w innych przestrzeniach.

Pierwszy przykład, który ci przedstawimy, może być nieco niejasny na pierwszy rzut oka, ale mamy nadzieję, że nam wybaczysz. Zaczynamy od tego bardzo ważnego typu przestrzeni: przestrzeni Minkowskiego. Powodem, dla którego ją wybraliśmy, to fakt, że jest bardzo powszechna w fizyce, w szczególności jest używana w teorii względności, a nawet w relatywistycznej kwantowej teorii pola. Przestrzeń ta jest bardzo podobna do przestrzeni euklidesowej, ale różni się od niej bardzo istotną cechą: dodaniem iloczynu skalarnego, zwanego również iloczynem wewnętrznym (nie mylić z iloczynem wektorowym).

Zarówno przestrzeń euklidesowa, jak i przestrzeń Minkowskiego są tym, co matematycy nazywają przestrzenią płaską. Oznacza to, że sama przestrzeń ma płaskie właściwości; na przykład najkrótsza odległość między dowolnymi dwoma punktami jest zawsze linią prostą między nimi (sprawdź Omni kalkulator interpolacji liniowej 🇺🇸). Istnieją jednak inne rodzaje przestrzeni matematycznych zwane przestrzeniami o niezerowej krzywiźnie, w których przestrzeń jest z natury zakrzywiona, a najkrótsza odległość między dwoma punktami nie jest linią prostą.

Taka zakrzywiona przestrzeń jest trudna do wyobrażenia w 3D, ale dla 2D możemy sobie wyobrazić, że zamiast płaskiej płaszczyzny mamy przestrzeń dwuwymiarową, na przykład zakrzywioną w kształcie powierzchni kuli. W takim przypadku dzieją się bardzo dziwne rzeczy. Najkrótsza odległość od jednego punktu do drugiego nie jest linią prostą, ponieważ każda linia w tej przestrzeni jest zakrzywiona z powodu wewnętrznej krzywizny przestrzeni. Inną bardzo dziwną cechą tej przestrzeni jest to, że niektóre linie równoległe 🇺🇸 w rzeczywistości spotykają się w pewnym punkcie. Możesz spróbować to zrozumieć, myśląc o południkach, które dzielą Ziemię na wiele stref czasowych i przecinają się na biegunach.

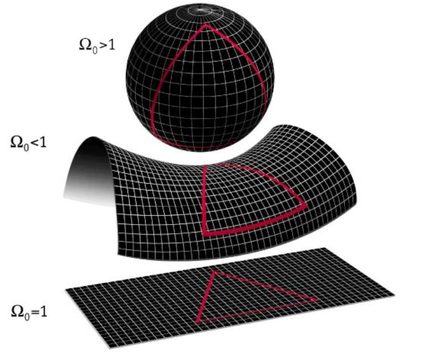
Ważne, aby pamiętać, że jest to ZASADNICZO coś innego od zamiany współrzędnych. Kiedy weźmiemy standardowe współrzędne $x, y, z$ i przekształcimy je na współrzędne biegunowe, cylindryczne lub nawet sferyczne, nadal będziemy w przestrzeni euklidesowej. Kiedy mówimy o przestrzeni zakrzywionej, mówimy o zupełnie innej przestrzeni pod względem jej wewnętrznych właściwości. We współrzędnych sferycznych nadal można mieć linię prostą, a odległość jest nadal mierzona w linii prostej, nawet jeśli byłoby to bardzo trudne do wyrażenia w liczbach.

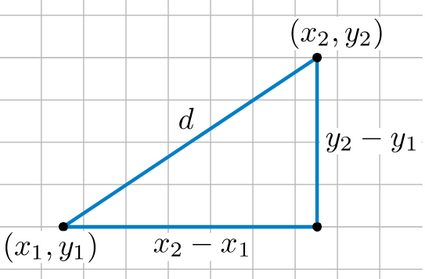
Wracając do przestrzeni euklidesowej, możemy teraz przedstawić wzór na odległość, który obiecaliśmy na początku. Równanie na odległość dwóch punktów to:

Bazuje ono na twierdzeniu Pitagorasa, które mówi, że $a^2+b^2=c^2$. Tutaj $a$ i $b$ są przyprostokątnymi trójkąta prostokątnego, a $c$ jest przeciwprostokątną. Załóżmy, że dwa punkty $(x_1, y_1)$ i $(x_2, y_2)$ są współrzędnymi punktów końcowych przeciwprostokątnej. Wówczas $(x_2 - x_1)^2$ w równaniu odległości odpowiada $a^2$, a $(y_2 - y_1)^2$ odpowiada $b^2$. Ponieważ $c = \sqrt{a^2 + b^2}$, to widać, dlaczego jest to po prostu rozszerzeniem twierdzenia Pitagorasa.

Wzór na odległość, który właśnie poznaliśmy, jest standardowym wzorem na odległość euklidesową, ale jeśli się nad tym zastanowić, może wydawać się nieco ograniczony. Często nie chcemy znaleźć tylko odległości między dwoma punktami. Czasami należy obliczyć odległość punktu od prostej lub okręgu. W takich przypadkach musimy najpierw zdefiniować punkt na tej prostej lub obwodzie, którego użyjemy do obliczenia odległości, a następnie użyć wzoru na odległość, który widzieliśmy powyżej.

Tutaj kluczowa staje się koncepcja prostej prostopadłej 🇺🇸. Odległość między punktem a obiektem ciągłym jest definiowana za pomocą prostopadłości. Z geometrycznego punktu widzenia, pierwszym krokiem do zmierzenia odległości od jednego punktu do drugiego jest utworzenie prostej między oboma punktami, a następnie zmierzenie długości tego odcinka. Kiedy mierzymy odległość od punktu do prostej, pojawia się pytanie „Którą z wielu możliwych prostych powinniśmy narysować?”. W tym przypadku odpowiedź brzmi: linia od punktu, która jest prostopadła do pierwszej prostej. Odległość ta wyniesie zero w przypadku, gdy punkt jest częścią prostej. Dla tych przypadków 1D możemy rozważyć tylko odległość między punktami, ponieważ prosta reprezentuje całą przestrzeń 1D.

To nakłada ograniczenia na sposób obliczania odległości w niektórych interesujących przypadkach geometrycznych. Na przykład, możemy przedefiniować pojęcie wysokości trójkąta tak, aby była to po prostu odległość od jednego wierzchołka do przeciwległego boku trójkąta. W tym przypadku pole trójkąta jest również przedefiniowane w kategoriach odległości, ponieważ pole jest funkcją wysokości trójkąta.

Spójrzmy na kilka przykładów w przestrzeni 2D. Aby obliczyć odległość między punktem a prostą, możemy przejść krok po kroku (wyznaczyć odcinek prostopadły do prostej zawierającej punkt i obliczyć jego długość) lub możemy po prostu użyć tego „poręcznego” równania:

gdzie prosta jest zadana równaniem ogólnym przez $Ax+By+C = 0$, a punkt jest zdefiniowany jako $(x_1, y_1)$.

Jedyny problem polega na tym, że linia prosta jest zwykle podawana z wykorzystaniem równania kierunkowego jako $y=mx+b$, więc musielibyśmy przekształcić to równanie do wcześniej pokazanej postaci:

więc widzimy, że $A=m$, $B=-1$ i $C=b$. Pozostawia to poprzednie równanie z następującymi wartościami:

Aby obliczyć odległość między dwiema prostymi, wystarczy wyznaczyć długość odcinka, który przechodzi od jednej do drugiej i jest do nich prostopadły. Ponownie, istnieje prosty wzór, który nam pomoże:

jeśli równania prostych są następujące: $A_1x+B_1y+C_1=0$ i $A_2x+B_2y+C_2=0$. Możemy również przekształcić to na wyrażenie wykorzystujące równania prostych w postaci kierunkowej i otrzymać:

dla prostych $y=m_1x+b_1$ i $y=m_2x+b_2$.

Zauważmy, że obie proste muszą być równoległe, gdyż w przeciwnym razie zetknęłyby się w jakimś punkcie i ich odległość wyniosłaby $d=0$. Jest to powód, dla którego wzory w postaci ogólnej pomijają większość indeksów, ponieważ dla linii równoległych: $A_1=A_2=A$ i $B_1=B_2=B$, podczas gdy w postaci kierunkowej proste równoległe to takie, dla których $m_1=m_2=m$.

Jak wspomnieliśmy wcześniej, odległość może oznaczać wiele rzeczy, dlatego w naszym kalkulatorze udostępniliśmy kilka różnych opcji. Możesz obliczyć odległość między punktem a linią prostą, odległość między dwiema prostymi (zawsze muszą być równoległe) lub odległość między punktami w przestrzeni. Jeśli chodzi o obliczanie odległości między dwoma punktami, masz możliwość zrobienia tego w 1, 2, 3 lub 4 wymiarach. Wiemy, wiemy, cztery wymiary brzmią przerażająco, ale nie musisz korzystać z tej opcji. Zawsze możesz dowiedzieć się więcej na ten temat, czytając interesujące pozycje i bawiąc się kalkulatorem. Obiecujemy, że nie zniszczy to internetu ani wszechświata.

Dodaliśmy również możliwość zdefiniowania 3 różnych punktów w przestrzeni, z których uzyskasz 3 pary odległości między nimi, więc jeśli masz więcej niż dwa punkty, zaoszczędzi to czas. Liczba wymiarów, w których pracujesz, określi liczbę współrzędnych opisujących punkt, dlatego wraz ze wzrostem liczby wymiarów kalkulator poprosi o podanie większej liczby wartości w odpowiednich polach.

Mimo że korzystanie z Omni kalkulatora odległości jest bardzo proste, zdecydowaliśmy się dołączyć rozwiązanie krok po kroku. W ten sposób możesz zapoznać się z równaniem na odległość i sposobem jego użycia (jakby to były lata 50., a internet wciąż nie istniał). Przyjrzyjmy się teraz praktycznemu przykładowi: Jak znaleźć odległość między dwoma punktami w przestrzeni dwuwymiarowej.

Załóżmy, że masz dwie współrzędne, $(3, 5)$ i $(9, 15)$ i chcesz obliczyć dystans między nimi. Aby obliczyć odległość 2D między tymi dwoma punktami, wykonaj następujące kroki:

1. Wprowadź wartości do wzoru: $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.

2. W równaniu odejmij wartości w nawiasach.

3. Podnieś do kwadratu obie wielkości w nawiasach.

4. Dodaj poszczególne wyniki.

5. Spierwiastkuj sumę.

6. Użyj Omni kalkulatora odległości, aby sprawdzić wyniki.

Po samodzielnym przeliczeniu przykładu otrzymamy:

co jest równe w przybliżeniu $11,\!66$. Zwróć uwagę, że gdy weźmiesz pierwiastek kwadratowy, otrzymasz wynik dodatni i ujemny, ale ponieważ masz do czynienia z odległością, interesuje cię tylko wynik dodatni. Kalkulator wykona te obliczenia krok po kroku, aby podać wynik dokładny i przybliżony.

Przyjrzyjmy się jednemu z zastosowań kalkulatora odległości. Załóżmy, że podróżujemy między miastami A i B, a jedyny przystanek znajduje się w mieście C, z trasą od A do B prostopadłą do trasy z B do C. Możemy określić odległość z A do B, co pomoże nam oszacować koszt paliwa, zużyte paliwo i koszt na osobę podczas podróży.

Trudność polega na dokładnym obliczeniu odległości między miastami. Linia prosta (jak ta, której używamy w tym kalkulatorze) może być dobrym przybliżeniem, ale może być dość błędna, jeśli trasa, którą wybierasz, nie jest bezpośrednia, ale wymaga objazdu, być może w celu ominięcia gór lub innego miasta. W takim przypadku wystarczy użyć map Google lub innego narzędzia, które oblicza odległość wzdłuż trasy, a nie tylko odległość z jednego punktu do drugiego w linii prostej.

Warto pamiętać, że nasz kalkulator odległości świetnie się sprawdza do oszacowania dystansu w linii prostej, a nie wzdłuż wyznaczonej trasy. Mając to na uwadze, nadal istnieje wiele scenariuszy, w których możesz być zainteresowany odległością między obiektami, niezależnie od ścieżki, którą należy pokonać. Jednym z takich przykładów jest odległość między obiektami astronomicznymi.

Kiedy patrzymy na odległości w obrębie naszej Ziemi, trudno jest zajść daleko w obliczeniach bez napotkania pewnych problemów, od wewnętrznej krzywizny tej przestrzeni (z powodu niezerowej krzywizny Ziemi) do ograniczonej maksymalnej odległości między dwoma punktami na Ziemi. To właśnie z tego powodu, a także dlatego, że istnieje cały wszechświat poza naszą Ziemią, odległości we wszechświecie są bardzo interesujące dla wielu ludzi. Ponieważ nie mamy odpowiednich środków do podróży międzyplanetarnych, nie mówiąc już o podróżach międzygwiezdnych, skupmy się na razie na rzeczywistej odległości euklidesowej do niektórych obiektów niebieskich. Na przykład odległości od Ziemi do Słońca lub odległości od Ziemi do Księżyca.

Odległości te są niewyobrażalne dla naszych umysłów. Z trudem pojmujemy rozmiar naszej planety, nie mówiąc już o rozległym, nieskończonym wszechświecie. Jest to tak trudne, że musimy używać notacji naukowej lub lat świetlnych, jako jednostki odległości dla tak dużych długości. Najdłuższe podróże, jakie można odbyć na Ziemi, to zaledwie kilka tysięcy kilometrów, podczas gdy odległość z Ziemi do Księżyca, najbliższego nam obiektu astronomicznego, wynosi średnio 384 000 km. Co więcej, odległość do naszej najbliższej gwiazdy, czyli odległość Ziemi od Słońca, wynosi 150 000 000 km, czyli nieco ponad 8 minut świetlnych.

Kiedy porównamy te odległości z odległością do naszej drugiej najbliższej gwiazdy (Alfa Centauri), która wynosi 4 lata świetlne, nagle zaczynają one wyglądać na znacznie mniejsze. Jeśli chcemy dokonać jeszcze bardziej absurdalnego porównania, zawsze możemy pomyśleć o locie z Nowego Jorku do Sydney, który zwykle zajmuje ponad 20 godzin i wynosi zaledwie nieco ponad 16 000 km, a następnie porównać go z rozmiarem obserwowalnego wszechświata, który wynosi około 46 600 000 000 lat świetlnych!

Tutaj nieumyślnie objawiliśmy fascynujący punkt, a mianowicie, że odległości mierzymy nie w długości, ale w czasie. W ten sposób rozszerzamy pojęcie odległości poza jej geometryczny sens. Zbadamy tę możliwość w następnym rozdziale, gdy będziemy mówić o znaczeniu i przydatności odległości poza czysto geometrycznym znaczeniem. Jest to bardzo interesująca ścieżka, która jest inspirowana głównie filozoficzną potrzebą rozszerzenia każdego pojęcia, aby miało uniwersalne znaczenie, a także wynika z oczywistej teorii fizycznej, o której należy wspomnieć, mówiąc o permutacjach przestrzeni i czasu lub każdej innej zmiennej, którą można zmierzyć.

Zazwyczaj pojęcie odległości odnosi się do geometrycznej odległości euklidesowej i jest powiązane z długością. Można jednak rozszerzyć definicję odległości, aby oznaczała tylko różnicę między dwiema rzeczami, a wtedy otwiera się cały świat możliwości. Nagle można zdecydować, jaki jest najlepszy sposób pomiaru odległości między dwiema rzeczami i ująć ją w kategoriach najbardziej użytecznej wielkości. Bardzo prostym krokiem jest zastanowienie się nad odległością między dwiema liczbami, która jest niczym innym jak różnicą 1D między tymi liczbami. Aby ją uzyskać, po prostu odejmujemy jedną od drugiej, a wynikiem jest różnica, czyli odległość.

Możemy przeskoczyć z tej liczbowej odległości do na przykład, różnicy lub odległości w kategoriach różnicy procentowej, co w niektórych przypadkach może zapewnić lepszy sposób porównania. To wciąż tylko jeden poziom abstrakcji, w którym po prostu usuwamy jednostki miary. Ale co by było, gdybyśmy użyli zupełnie innych jednostek?

Rozszerzając pojęcie odległości, aby oznaczało coś bliższego różnicy, możemy obliczyć różnicę między dwiema temperaturami lub inną powiązaną wielkością, taką jak ciśnienie. Ale nie musimy popadać w skrajności, zobaczmy, jak dwa punkty mogą być oddzielone inną odległością, w zależności od przyjętych założeń. Wracając do przykładu z odległością jazdy samochodem, możemy zmierzyć odległość podróży w czasie, zamiast w długości. W tym przypadku potrzebujemy założenia, aby umożliwić takie tłumaczenie; mianowicie sposób transportu.

Istnieje duża różnica w czasie potrzebnym na pokonanie 10 km samolotem w porównaniu do czasu potrzebnego na podróż samochodem. Czasami jednak założenie jest jasne i domyślnie uzgodnione, na przykład gdy mierzymy odległość błyskawicy w czasie, który następnie przeliczamy na długość. To prowadzi do interesującej kwestii, że współczynnik konwersji między odległościami w czasie i długości jest tym, co nazywamy „szybkością” lub „prędkością” (pamiętaj, że nie są one dokładnie tym samym). Prawdę powiedziawszy, ta szybkość nie musi być stała, czego przykładem są ruchy z przyspieszeniem, takie jak swobodne spadanie pod wpływem siły grawitacji, lub ten, który łączy czas zatrzymania i odległość zatrzymania poprzez siłę hamującą i opór powietrza lub, w bardzo ekstremalnych przypadkach, poprzez siłę zderzenia samochodu.

Innym miejscem, w którym można znaleźć dziwne jednostki odległości, jest fizyka ciała stałego, gdzie odległość, jaką cząstka pokonuje wewnątrz materiału, jest często wyrażana jako średnia liczba interakcji lub zderzeń. Odległość ta jest powiązana z długością za pomocą średniej drogi swobodnej, która jest średnią odległością (dystansem), jaką cząstka pokonuje między kolejnymi interakcjami. Jeśli chcemy stać się jeszcze bardziej egzotyczni, możemy pomyśleć o odległości od obecnej wartości do przyszłej wartości czegoś takiego jak samochód.

Nie chcemy jednak nikomu zbytnio zamieszać w głowie, więc proszę, nie myśl o tym zbyt mocno. Po prostu weź nasz kalkulator i użyj go dla odległości opartej na długości w przestrzeni dwuwymiarowej. Zawsze możesz wrócić do tego filozoficznego poglądu na odległości, jeśli kiedykolwiek się znudzisz!

Aby znaleźć odległość między dwoma punktami, użyjemy wzoru na odległość: √[(x₂ - x₁)² + (y₂ - y₁)²]:

1. Określ współrzędne obu punktów w przestrzeni.

2. Odejmij osobno współrzędne x i y jednego punktu od współrzędnych drugiego punktu.

3. Podnieś obie różnice do kwadratu.

4. Zsumuj wartości otrzymane w poprzednim kroku.

5. Znajdź pierwiastek kwadratowy z powyższego wyniku.

Jeśli uważasz, że to zbyt duży wysiłek, możesz po prostu użyć Omni kalkulatora odległości.

Odległość nie jest wektorem. Odległość między punktami jest wielkością skalarną, co oznacza, że jest definiowana tylko przez jej wartość. Natomiast przemieszczenie jest wektorem z wartością i kierunkiem. Tak więc odległość między punktami A i B jest taka sama jak odległość od punktu B do punktu A, ale przemieszczenie jest różne w zależności od ich kolejności.

Jedna mila angielska to 1609,344 metrów, natomiast jedna mila morska to 1852 metry. Mile i jednostki pochodne (np. mile na godzinę) są powszechnie używane w krajach wykorzystujących imperialny system miar.

Wzór na odległość to: √[(x₂ - x₁)² + (y₂ - y₁)²]. Działa on dla dowolnych dwóch punktów w przestrzeni 2D o współrzędnych (x₁, y₁) dla pierwszego punktu i (x₂, y₂) dla drugiego punktu. Można to łatwo zapamiętać, jeśli zauważy się, że jest to twierdzenie Pitagorasa, gdzie odległość jest przeciwprostokątną, a długości przyprostokątnych odpowiadają różnicom między składowymi x i y punktów.

Długość wektora to jego moduł. Jeśli znasz jego składowe:

1. Weź każdą ze składowych wektora i podnieś ją do kwadratu.

2. Zsumuj je.

3. Znajdź pierwiastek kwadratowy z poprzedniego wyniku.

4. To wszystko — gratulacje!

Jeśli znasz jego współrzędne biegunowe, będzie to promień i kąt. Wartość promienia jest długością wektora.

Jednostką odległości w układzie SI jest metr, w skrócie „m”. Inne powszechne jednostki w Międzynarodowym Układzie Jednostek to między innymi centymetr (jedna setna metra) i kilometr (tysiąc metrów).

Odległość od punktu A do punktu B to długość linii prostej biegnącej od punktu A do punktu B. Odległość od punktu B do punktu A jest taka sama jak odległość od punktu A do punktu B, ponieważ odległość jest skalarem.

Odległość jest miarą jednowymiarowej przestrzeni. Odległość między dwoma punktami to najkrótsza długość przestrzeni 1D między nimi. Jeśli podzielisz odległość przez czas, otrzymasz szybkość, która ma wymiary przestrzeni w czasie.

Rok świetlny jest miarą odległości. Jest to 9,461·10¹² kilometrów lub 5,879·10¹² mil, czyli odległość pokonywana przez promień światła w idealnej próżni w ciągu jednego roku.

Odległość można wyznaczyć na podstawie prędkości i czasu poruszania się obiektu:

1. Upewnij się, że prędkość i czas mają zgodne jednostki (kilometry na godzinę i godziny, metry na sekundę i sekundy, itd.).

2. Jeśli nie, przelicz je na odpowiednie jednostki.

3. Pomnóż prędkość przez czas.

4. Wynikiem powinna być przebyta odległość w jednostkach długości, które były zawarte w prędkości!