Kalkulator wzrostu wykładniczego
Jest bardzo wiele procesów, w których analizie pomoże ci nasz Omni kalkulator wzrostu wykładniczego. Ogólna zasada mówi, że wzoru na wzrost wykładniczy:
używamy, gdy istnieje pewna wielkość o wartości początkowej, , która zmienia się w czasie, , ze stałym tempem zmian, . Funkcja wykładnicza pojawiająca się w powyższym wzorze ma podstawę równą .
Należy pamiętać, że wykładnicze tempo wzrostu, , może być dowolną liczbą dodatnią, ale nasz kalkulator działa również jako kalkulator zaniku wykładniczego — gdzie reprezentuje również tempo rozkładu, które powinno wynosić od 0 do -100%. Wynika to z faktu, że nie można uzyskać spadku o więcej niż 100% w odniesieniu do początkowej ilości, ponieważ oznaczałoby to spadek do wartości ujemnych.
Równanie wzrostu wykładniczego jest używane w datowaniu radiowęglowym 🇺🇸, reakcji łańcuchowej polimerazy (PCR, ang. polymerase chain reaction, możesz poczytać o tym więcej w naszym kalkulatorze temperatury wyżarzania 🇺🇸), a także w obliczaniu odsetek składanych. Aby dowiedzieć się więcej, zobacz nasz kalkulator procentu składanego. Więcej przykładów zastosowania tej formuły zobaczysz w dalszej części tekstu.
Jak obliczyć wzrost wykładniczy
Rozważmy następujący problem: populacja małego miasta na początku 2019 roku wynosiła 10 000 osób. Zauważono, że populacja miasta rośnie w stałym tempie 5% rocznie. Co należy zrobić, aby obliczyć prognozowaną liczbę ludności w roku 2030? Z podanych danych możemy wywnioskować, że początkowa wartość populacji, , wynosi 10 000. Ponadto stopa wzrostu wynosi .
Dlatego wzór na wzrost wykładniczy, który powinniśmy użyć, to:
Tutaj jest liczbą lat, które upłynęły od 2019 roku. W naszym przypadku, dla roku 2030, powinniśmy użyć , ponieważ jest to różnica w liczbie lat między rokiem 2030 a początkowym rokiem 2019. Ostatecznie otrzymujemy:
Tak więc widzimy, że prognozowana liczba mieszkańców naszego małego miasta w 2030 roku wynosi około 17 103.
Jeśli chcesz zagłębić się w ten konkretny wzór, możesz skorzystać z naszego kalkulatora wzrostu wykładniczego, aby sprawdzić prognozowaną liczbę mieszkańców dla każdego roku, począwszy od 2019 roku. Wynikiem tych obliczeń jest poniższa tabela, w której zaokrąglamy wyniki do najbliższej liczby całkowitej:
Rok | t | x(t) |
|---|---|---|
2019 | 0 | 10 000 |
2020 | 1 | 10 500 |
2021 | 2 | 11 025 |
2022 | 3 | 11 576 |
2023 | 4 | 12 155 |
2024 | 5 | 12 763 |
2025 | 6 | 13 401 |
2026 | 7 | 14 071 |
2027 | 8 | 14 775 |
2028 | 9 | 15 513 |
2029 | 10 | 16 289 |
2030 | 11 | 17 103 |
Jeśli chcesz jeszcze lepiej zobrazować wzrost populacji, możesz przedstawić te dane graficznie, z osią poziomą będącą osią czasu i osią pionową reprezentującą wartość populacji . Dane z tabeli są punktami leżącymi na wykresie funkcji
wykładniczej:
Ponieważ podstawa tej funkcji wykładniczej wynosi 1,05 i jest większa od 1, otrzymany wykres wzrostu wykładniczego jest rosnący. Główną różnicą między tym wykresem a zwykłym wykresem funkcji wykładniczej jest to, że jego punkt przecięcia y nie wynosi 1, ale 10 000, co odpowiada wartości początkowej :
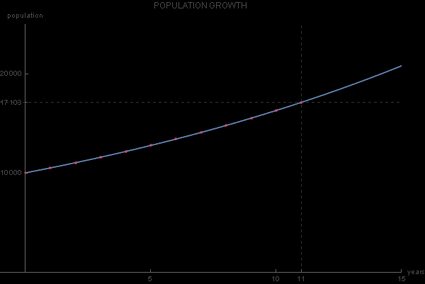
Na tym przykładzie widzimy możliwe ograniczenia modelu wzrostu wykładniczego — jest nierealne, aby tempo wzrostu pozostało stałe w czasie. Mianowicie, trudno oczekiwać, że roczne tempo wzrostu populacji miasta utrzyma się na poziomie 5% przez dekadę lub dłużej.
W rzeczywistych sytuacjach występują naturalne oscylacje tempa wzrostu, które nie są uwzględnione w tym modelu wzrostu wykładniczego. Bardziej realistycznym modelem wzrostu populacji jest logistyczny model wzrostu, który bierze pod uwagę pojemność środowiska, czyli stałą reprezentującą naturalny limit wzrostu populacji.
Jak znaleźć moment, w którym początkowa ilość osiąga daną wartość?
Kontynuując rozważania na temat naszego małego miasta, kolejnym pytaniem, jakie możemy sobie zadać, jest „kiedy możemy spodziewać się, że populacja osiągnie pewną istotną wartość?” Jest to przydatne, jeśli chcesz dostosować planowanie urbanistyczne miasta do większej liczby ludności, więc rada miasta musi wiedzieć, w którym roku może spodziewać się potrojenia liczby ludności miasta w stosunku do pierwotnych 10 000?
W tym przypadku wiemy, ile wynosi , ale nie znamy wartości , kiedy to nastąpi. Zróbmy to krok po kroku:
-
Wstaw do wzoru:
-
Po podzieleniu obu stron równania przez 10 000 otrzymujemy: .
-
Weźmy logarytm o podstawie 1,05 z obu stron tego równania: .
-
Oblicz logarytm, aby ostatecznie otrzymać: .
Tak więc odpowiedzią na pytanie rady jest, że liczba mieszkańców naszego miasta potroi się w trakcie około 22 lat po początkowym roku 2019, czyli w 2041 roku:
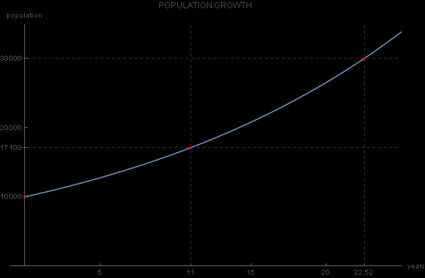
Czy czas może mieć ujemną wartość?
Być może zauważyłeś/aś już problem dotyczący wykładniczego wzrostu i rozpadu, że naturalnie traktuje on czas jako wartość dodatnią, więc przewidujemy przyszłą wielkość. Nie przeszkadza nam to jednak w stosowaniu tego wzoru z ujemnymi wartościami czasu! Oznacza to, że opisujemy interesujące nas zjawisko w czasie przed dokonaniem początkowej obserwacji.
W przypadku wzrostu populacji można zadać pytanie: jaka była populacja naszego małego miasta w 2000 roku, zakładając, że stopa wzrostu populacji wynosiła stale 5%?
Aby to rozwiązać, należy użyć , ponieważ rok 2000 poprzedza rok 2019 o 19 lat. Odpowiedź brzmiałaby zatem:
mieszkańców, co widać również na poniższym wykresie:
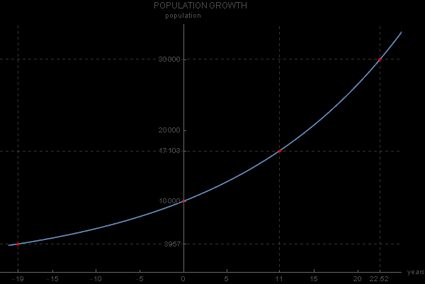
Alternatywny sposób zapisu równania wzrostu wykładniczego
W niektórych zastosowaniach, na przykład przy obliczaniu rozpadu wykładniczego substancji promieniotwórczej, bardziej wydajny jest alternatywny sposób zapisu wzoru na wykładniczy wzrost i rozpad:
Współczynnik odgrywa rolę tempa wzrostu, podobnie jak w oryginalnym wzorze na wzrost wykładniczy. Porównując powyższe równanie z oryginalnym, można zauważyć, że zależność między i jest następująca:
co oznacza, że:
i .
Przykład zastosowania wzoru na rozkład wykładniczy
Rozpad radioaktywny jest dobrze znanym przykładem zastosowania wzoru wykładniczego. Dla danej początkowej ilości substancji radioaktywnej można zapisać prawo rządzące jej rozpadem w czasie. Przykładem z życia codziennego będzie zmierzenie ilości kawy pozostającej w organizmie o 22:00, jeśli wypiłeś filiżankę kawy z kofeiny w południe.
Wykorzystamy fakt, że okres połowicznego rozpadu kofeiny w ludzkim organizmie wynosi około sześciu godzin. Okres półtrwania jest definiowany jako czas potrzebny danej ilości do zmniejszenia się do połowy jej początkowej wartości. Tak więc w tym przykładzie mamy
W tym przypadku łatwiej będzie użyć alternatywnej notacji dla wzoru na wzrost wykładniczy:
.
Prześledź obliczenia krok po kroku:
-
Wstaw x(6)= 47,5 i t = 6 do równania: .
-
Wyrażenie to, po podzieleniu obu stron równania przez 95 i zastosowaniu logarytmu naturalnego, daje: .
-
Stosując logarytm naturalny, otrzymujemy: .
-
Dlatego wzór na rozkład wykładniczy w naszym przykładzie brzmi: .
-
Ponieważ godzina 22:00 jest dziesięć godzin później niż południe, chcemy znać ilość kofeiny w . Mamy: .
Tak więc o godzinie 22:00 ilość kofeiny pozostałej w organizmie będzie wynosić około 30 mg.
A co zrobić, jeśli w ogóle nie ma podanego czasu?
Czas może być wyrażony w dowolnych jednostkach. Dla niektórych problemów będą to sekundy, dla innych lata. Należy wybrać jednostkę czasu w sposób odpowiadający naturze obserwowanego procesu. Na przykład, jeśli chcesz zrozumieć zmiany w populacji miasta, powinieneś/aś wybrać lata. Z drugiej strony, jeśli zamierzasz obliczyć ilość kawy pozostałej w twoim ciele po wypiciu filiżanki, odpowiednią jednostką czasu powinny być godziny lub minuty.
Należy pamiętać, że nie musi być traktowane wyłącznie jako czas. W niektórych przypadkach zmienna mierząca tempo zmian może być inna niż czas. Na przykład, podczas badania sposobu, w jaki ciśnienie atmosferyczne zmienia się wraz z wysokością, zmienną mierzącą tę zmianę jest odległość i należy wybrać metry jako odpowiednie jednostki zmiany. Nasz kalkulator ciśnienia atmosferycznego na danej wysokości 🇺🇸 może tu pomóc.
Jak różne wykładnicze tempa wzrostu wpływają na wzrost
Różnica w wykładniczym tempie wzrostu r będzie miała znaczący wpływ na to, jak szybko obserwowana wielkość zmieni się od wartości początkowej. Zacznijmy od i, korzystając z kalkulatora wzrostu wykładniczego, zobaczmy, jakie będzie dla czterech różnych wartości :
r | x0 | x(10) |
|---|---|---|
1% | 100 | 110,5 |
3% | 100 | 134,4 |
5% | 100 | 162,9 |
10% | 100 | 259,4 |
Z powyższej tabeli widzimy, że wszystkie wartości początkowe są takie same, równe , ale ostateczne wartości różnią się znacząco. Intuicja może cię tutaj oszukać, ponieważ różnica między 1% a 3% nie wygląda na dużą, ale po dziesięciu okresach oznacza to o 21,67% wyższą wartość dla 3% wzrostu w porównaniu do 1% wzrostu.
Jeśli porównamy 10% wzrost z 5% wzrostem, zauważymy jeszcze większą różnicę, 59,23% na korzyść 10% wzrostu. Kontrast ten można zaobserwować na poniższej graficznej reprezentacji czterech funkcji wzrostu wykładniczego:
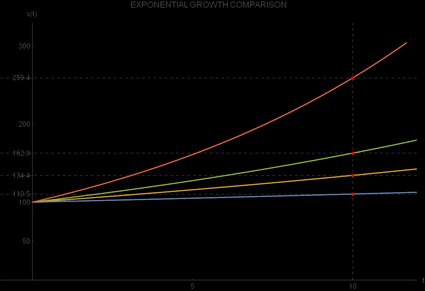
Jakie są rzeczywiste zastosowania wzrostu wykładniczego?
Wzór na wykładniczy wzrost i zanik jest używany do modelowania różnych zjawisk w świecie rzeczywistym, takich jak:
- wzrost populacji bakterii, wirusów, roślin, zwierząt i ludzi,
- rozpad materii radioaktywnej,
- stężenie leków we krwi,
- ciśnienie atmosferyczne powietrza na określonej wysokości,
- procent składany i wzrost gospodarczy,
- datowanie radiowęglowe,
- moc obliczeniowa komputerów itp.
💡 Czy wiesz, że...
Możesz sprawdzić, czy zbiór liczb jest zgodny ze wzorem na wzrost wykładniczy, korzystając z dobrze znanego prawa Benforda?
Źródła
FAQs
Jak obliczyć wzrost wykładniczy?
Wzrost wykładniczy jest opisany wzorem:
Xt = X0 ⋅ (1 + r/100)ᵗ
gdzie Xt jest wielkością w czasie t, X₀ jest wartością początkową, r jest tempem zmian.
Jaka jest różnica między wzrostem wykładniczym a liniowym?
Wzrost wykładniczy następuje poprzez pomnożenie wartości początkowej przez pewien stały czynnik w każdym kroku czasowym. Liniowy wzrost oznacza, że dodajemy tę samą wartość w każdym kroku czasowym.
Jak obliczyć rozkład wykładniczy?
Rozkład wykładniczy jest określony wzorem:
Xt = X0 ⋅ exp(μt)
gdzie Xt jest wielkością w czasie t, X₀ jest wielkością początkową, a μ jest stałą rozkładu.