Kalkulator prawdopodobieństwa
Za pomocą kalkulatora prawdopodobieństwa można badać relacje prawdopodobieństwa między dwoma niezależnymi zdarzeniami. Na przykład, jeśli wiemy, że szansa na wystąpienie zdarzenia A to 50% i taka sama jest szansa wystąpienia niezależnego zdarzenia B, to jakie są szanse na wystąpienie obu tych zdarzeń, tylko jednego z nich, co najmniej jednego z nich, żadnego z nich itd.
Nasz kalkulator prawdopodobieństwa przewiduje sześć scenariuszy, plus 4 dodatkowe, gdy wprowadzisz parametr liczby rzutów monetą, tzn. liczbę prób, które bierzemy pod uwagę. Gdy znasz prawdopodobieństwa zdarzeń A i B, nasz kalkulator pozwoli ci zaoszczędzić mnóstwo czasu.
Czytając dalej ten artykuł:
- Nauczysz się prawidłowo korzystać z Omni kalkulatora prawdopodobieństwa;
- Dowiesz się, jak znaleźć prawdopodobieństwa pojedynczych zdarzeń;
- Zapoznasz się z wieloma przykładami użycia prawdopodobieństwa, w tym z pojęciem prawdopodobieństwa warunkowego;
- Poznasz różnicę między prawdopodobieństwem teoretycznym a empirycznym; oraz
- Poszerzysz swoją wiedzę na temat związku między prawdopodobieństwem a statystyką.
A może trafiłeś/aś tutaj, by ocenić szanse na wygranie zakładu lub trafienie jackpota? Nasz kalkulator szans i kalkulator loterii 🇺🇸 na pewno się przydadzą!
Jak znaleźć prawdopodobieństwo zdarzeń? - definicja prawdopodobieństwa
Podstawową definicją prawdopodobieństwa jest stosunek wszystkich korzystnych wyników do liczby wszystkich możliwych wyników.
Dozwolone wartości pojedynczego prawdopodobieństwa zawierają się w przedziale od 0 do 1, często zapisuje się je również zapisywać jako wartości procentowe. Prawdopodobieństwo pojedynczego zdarzenia można wyrazić w następujący sposób:
- Prawdopodobieństwo
A:P(A), - Prawdopodobieństwo
B:P(B), - Prawdopodobieństwo
+:P(+), - Prawdopodobieństwo
♥:P(♥)itd.
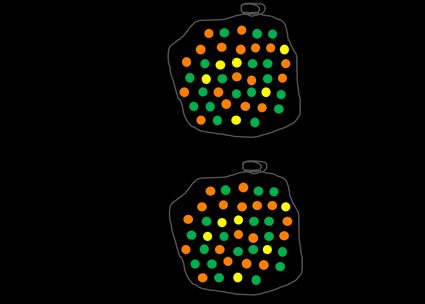
Przyjrzyjmy się przykładowi z wielokolorowymi kulkami. Mamy worek wypełniony pomarańczowymi, zielonymi i żółtymi kulkami. Nasze zdarzenie A to wybranie losowej kulki z torby. Możemy zdefiniować Ω jako zbiór wszystkich piłek. Prawdopodobieństwo zdarzenia Ω, czyli wybrania dowolnej kuli, wynosi oczywiście 1.
Spójrzmy teraz na coś trudniejszego — jakie jest prawdopodobieństwo wybrania pomarańczowej kuli? Aby odpowiedzieć na to pytanie, musisz wyznaczyć liczbę wszystkich pomarańczowych kulek i podzielić ją przez liczbę wszystkich kulek w torbie. Możesz to zrobić dla dowolnego koloru, np. żółtego, i bez wątpienia zauważysz, że im więcej kulek w danym kolorze, tym większe prawdopodobieństwo wybrania go z worka (o ile proces losowanie jest uczciwy).
Sprawdź nasz kalkulator prawdopodobieństwa 3 zdarzeń 🇺🇸 i kalkulator prawdopodobieństwa warunkowego 🇺🇸, aby dowiedzieć się, jak określać szanse wielu zdarzeń.

Możemy zdefiniować zdarzenie uzupełniające, zapisane jako Ā lub A', co oznacza nie A. W naszym przykładzie prawdopodobieństwo wylosowania **NIEpomarańczowej kuli jest oceniane jako liczba wszystkich niepomarańczowych kul podzielona przez liczbę wszystkich kul. Suma P(A) + P(Ā) zawsze wynosi 1, ponieważ nie ma innej opcji, takiej jak połowa kuli lub kula półpomarańczowa. Innymi słowy, zdarzenia A i Ā stanowią w sumie zdarzenie pewne.
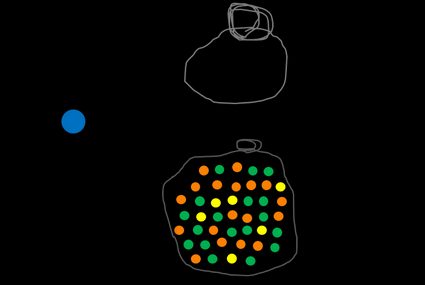
Teraz spróbujmy znaleźć prawdopodobieństwo otrzymania niebieskiej kuli. Bez względu na to, jak bardzo będziesz się starać, nie uda ci się nigdy jej wylosować, ponieważ w worku nie ma ani jednej niebieskiej kuli. Prawdopodobieństwo jest więc równe 0.
Cały czas używamy intuicyjnych obliczeń prawdopodobieństwa. Wiedza na temat ilościowego określania prawdopodobieństwa jest niezbędna do analizy statystycznej. Biorąc pod uwagę dyskretny zbiór danych, możemy uznać względną częstotliwość 🇺🇸 każdego wyniku jako prawdopodobieństwo jego wystąpienia.
Szukasz czegoś nieco innego? Sprawdź nasz kalkulator prawdopodobieństwa po teście 🇺🇸. 🎲
Jak korzystać z kalkulatora prawdopodobieństwa?
Aby w pełni wykorzystać możliwości naszego kalkulatora, wykonaj następujące kroki:
1. Zdefiniuj problem, który chcesz rozwiązać. Twój problem musi być skondensowany do dwóch niezależnych zdarzeń.
2. Znajdź prawdopodobieństwo każdego zdarzenia.
Wiesz już, jak oszacować prawdopodobieństwo pojedynczego zdarzenia, zatem do dzieła.
3. Wpisz procentowe prawdopodobieństwo każdego zdarzenia w odpowiednie pola.
Po ich wprowadzeniu Omni kalkulator prawdopodobieństwa natychmiast wyświetli dokładne prawdopodobieństwo następujących 6 scenariuszy:
- Wystąpią oba zdarzenia.
- Wystąpi co najmniej jedno ze zdarzeń.
- Wystąpi dokładnie jedno ze zdarzeń.
- Żadne ze zdarzeń się nie wydarzy.
- Tylko pierwsze zdarzenie się nie wydarzy.
- Tylko drugie zdarzenie się nie wydarzy.
Kalkulator pokaże również prawdopodobieństwo czterech innych scenariuszy, biorąc pod uwagę określoną liczbę prób:
- A zawsze się zdarzy;
- A nigdy się nie zdarzy;
- B zawsze się zdarzy;
- B nigdy się nie zdarzy;
Możesz zmienić liczbę prób i dowolne inne pole w kalkulatorze, a pozostałe pola automatycznie się przeliczą. Ta funkcja oszczędza mnóstwo czasu, np. jeśli chcesz ustalić, jakie musiałoby być prawdopodobieństwo zdarzenia B, aby prawdopodobieństwo wystąpienia obu zdarzeń wynosiło 50%.
Jeśli wszystkich możliwych wyników jest bardzo dużo i tylko kilka z nich to zdarzenia sprzyjające zdarzeniu A, to wartość prawdopodobieństwa jest bardzo mała, np. P(A) = 0,0001. Wygodnie jest używać wtedy notacji naukowej, aby nie pomylić liczby zer.
Prawdopodobieństwo warunkowe
Jedną z najważniejszych kwestii w świecie prawdopodobieństwa jest ustalenie, czy dane zdarzenia są zależne, czy nie. Dwa zdarzenia są niezależne, jeśli wystąpienie pierwszego z nich nie wpływa na prawdopodobieństwo wystąpienia drugiego. Na przykład, jeśli rzucimy idealnie wyważoną standardową sześcienną kostką, prawdopodobieństwo otrzymania dwójki ⚁ jest równe 1/6 (takie samo jak otrzymanie czwórki ⚃ lub jakiejkolwiek innej liczby).
Załóżmy, że rzucasz dwa razy kostką i za pierwszym razem wypadła piątka ⚄. Jeśli zadasz sobie pytanie, jakie jest prawdopodobieństwo uzyskania dwójki ⚁ w drugim rzucie, odpowiedź brzmi ponownie 1/6 z powodu niezależności tych zdarzeń.
Sposób myślenia, a także obliczenia, zmieniają się, jeśli jedno ze zdarzeń wypływa na cały system. Mówimy o prawdopodobieństwie warunkowym.
Powiedzmy, że mamy 10 różnych ponumerowanych kul bilardowych, od ➀ do ➉. Wybierając losową kulę, z prawdopodobieństwem dokładnie 1/10 otrzymamy ➆. Załóżmy, że wybieramy trójkę ➂ i usuwamy ją z gry. Ponownie zadajemy sobie pytanie, jaka jest szansa na uzyskanie siódemki ➆. Sytuacja zmieniła się, ponieważ jest jedna kulka z ➆ na dziewięć możliwości, co oznacza, że prawdopodobieństwo wybrania ➆ wynosi teraz 1/9. Innymi słowy, można zadać pytanie: „Jakie jest prawdopodobieństwo wybrania ➆, JEŚLI pierwszą wybraną kulą było ➂?”
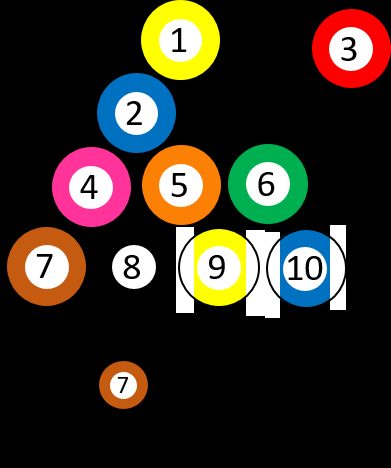
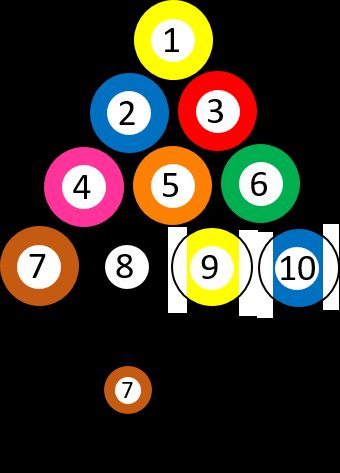
Spójrzmy na inny przykład: wyobraź sobie, że zamierzasz przystąpić do egzaminu ze statystyki. Wiesz od swoich starszych kolegów, że jest on dość wymagający, a prawdopodobieństwo, że zdasz w pierwszym terminie wynosi 0,5 (18 z 36 studentów zdało w zeszłym roku). W takim razie zadajmy sobie pytanie: „Jakie jest prawdopodobieństwo, że zdasz, JEŚLI choć trochę znasz temat?” W zeszłym roku 20 osób przyznało się do przejrzenia notatek przynajmniej raz przed egzaminem, a 16 z nich zdało, co oznacza, że odpowiedź na ostatnie pytanie wynosi 0,8. Wynik ten wskazuje, że ten dodatkowy warunek (uczenie się) naprawdę ma znaczenie jeśli chodzi o szanse powodzenia na egzaminie.
Jeśli nadal nie czujesz koncepcji prawdopodobieństwa warunkowego, spróbujmy na innym przykładzie: musisz przejechać samochodem z miasta X do miasta Y. Odległość między nimi wynosi około 150 km. Na pełnym baku można zwykle przejechać do 400 km. Jeśli nie znasz poziomu paliwa, możesz oszacować prawdopodobieństwo pomyślnego dotarcia do celu bez tankowania. A co jeśli dowiesz się, że ktoś właśnie zatankował twój samochód? Teraz masz niemal pewność, że uda ci się dotrzeć do celu... Chyba że inne czynniki ci to uniemożliwią!
Wzór na prawdopodobieństwo warunkowe
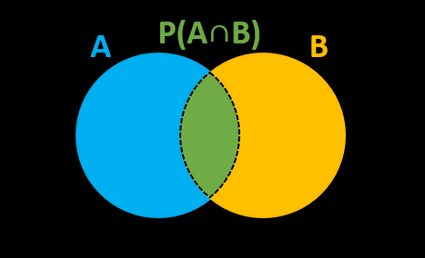
Formalnie, prawdopodobieństwo warunkowe, które oznaczamy jako P(A|B) lub PB(A), można obliczyć jako:
P(A|B) = P(A∩B) / P(B),
gdzie P(B) jest prawdopodobieństwem zdarzenia B, a P(A∩B) jest prawdopodobieństwem wystąpienia obu zdarzeń.
Z drugiej strony, możemy obliczyć prawdopodobieństwo wystąpienia obu zdarzeń, jeśli znamy jedno z prawdopodobieństw warunkowych:
P(A∩B) = P(A|B) × P(B)lubP(A∩B) = P(B|A) × P(A).
Koncepcję prawdopodobieństwa warunkowego można wygodnie przedstawić za pomocą drzewek. Pytamy uczniów w klasie, czy lubią matematykę i fizykę. Zdarzenie M oznacza procent uczniów, którzy lubią matematykę, a P procent uczniów, którzy lubią fizykę:

Istnieje słynne twierdzenie, które łączy warunkowe prawdopodobieństwa dwóch zdarzeń. Nazywa się ono twierdzeniem Bayesa, a jego formuła jest następująca:
P(A|B) = P(B|A) × P(A) / P(B)
Odpowiada ono na pytanie: „Jakie jest prawdopodobieństwo A pod warunkiem B, jeśli znam prawdopodobieństwo B pod warunkiem A oraz prawdopodobieństwa (niewarunkowe) poszczególnych zdarzeń?”.
Twierdzenie to czasami daje zaskakujące i nieintuicyjne wyniki. Najczęściej opisywanymi przykładami są testy narkotykowe i wykrywanie chorób, które mają wiele wspólnego ze względnym ryzykiem zachorowania w populacji. Skupmy się na tym drugim. W grupie 1000 osób mamy 10 chorych na rzadką chorobę. Wszyscy przeszli test, który wykazał prawdziwy wynik w 95% przypadków. Teraz chcemy znaleźć prawdopodobieństwo, że dana osoba choruje, jeśli wynik testu był pozytywny.
Odpowiadając intuicyjnie i bez głębszego zastanowienia, wiele osób powie, że wynik powinien wynosić około 90%. Brzmi rozsądnie, prawda? Wykonajmy kilka obliczeń i oszacujmy prawidłową odpowiedź.
- Będziemy używać notacji:
H- zdrowy,I- chory,+- test pozytywny,-- test negatywny. - Przepisujemy informacje z powyższego tekstu w postaci prawdopodobieństwa:
P(H) = 0,99,P(I) = 0,01,P(+|I) = 0,95,P(-|I) = 0,05,P(+|H) = 0,05,P(-|H) = 0,95. - Obliczamy całkowite prawdopodobieństwo pozytywnego wyniku testu:
P(+) = P(+|I) × P(I) + P(+|H) × P(H) = 0,95 × 0,01 + 0,05 × 0,99 = 0,059. - Użyjemy teraz twierdzenia Bayesa, aby znaleźć prawdopodobieństwo warunkowe
P(I|+) = P(+|I) × P(I) / P(+) = 0,95 × 0,01 / 0,059 = 0,161.
Hmm... wynik nie jest aż tak wysoki, jak nam się wydawało, prawda? Okazuje się, że ten rodzaj paradoksu pojawia się, gdy istnieje znacząca nierównowaga między liczbą osób zdrowych i chorych lub ogólnie między dwiema różnymi grupami. Jeśli wynik testu jest pozytywny, zamiast wpadać w panikę lepiej powtórzyć test, aby móc postawić właściwą diagnozę.
Rozkład prawdopodobieństwa i dystrybuanta
Wyróżniamy dwa rodzaje rozkładów prawdopodobieństwa, w zależności od tego, czy zmienne losowe są dyskretne, czy ciągłe.
- Dyskretny rozkład prawdopodobieństwa opisuje prawdopodobieństwo wystąpienia przeliczalne wielu odrębnych wyników. Jednym z przykładów jest rozkład dwumianowy, który uwzględnia prawdopodobieństwo sukcesu w wielu próbach, np. podczas rzucania monetą. Inny przykład to rozkład Pascala (znany również jako rozkład ujemny dwumianowy), gdzie ustalona jest liczba sukcesów, a chcemy oszacować całkowitą liczbę prób. Kolejnym przykładem dyskretnego rozkładu prawdopodobieństwa jest rozkład Poissona. Jest on w rzeczywistości szczególnym przypadkiem rozkładu dwumianowego, możesz dowiedzieć się o nim więcej za pomocą naszego kalkulatora rozkładu Poissona 🇺🇸.
Funkcja masy prawdopodobieństwa może być interpretowana jako definicja rozkładu dyskretnego — przypisuje ona prawdopodobieństwo każdemu z możliwych wyników. Rozkład geometryczny 🇺🇸 jest doskonałym przykładem zastosowania funkcji masy prawdopodobieństwa.
- Ciągły rozkład prawdopodobieństwa przechowuje informacje o niepoliczalnych zdarzeniach. Nie można wówczas przewidzieć prawdopodobieństwa pojedynczego wyniku (jak w przypadku rozkładu dyskretnego), ale możemy znaleźć prawdopodobieństwo tego, że wynik znajdzie się w pewnym przedziale wartości. Odpowiednikiem funkcji masy prawdopodobieństwa jest funkcja gęstości rozkładu.
Rozkład normalny jest najbardziej znanym rozkładem ciągłym. Opisuje on szereg właściwości w dowolnej wystarczająco licznej populacji, np. wzrost dorosłych ludzi lub rozpowszechnienie IQ. Jego funkcją gęstości jest słynna krzywa dzwonowa Gaussa.
Jeśli masz bardziej zaawansowaną wiedzę w zakresie rachunku prawdopodobieństwa, z pewnością znasz też rozkład SMp(x) 🇺🇸, który uwzględnia kombinację kilku dyskretnych i ciągłych rozkładów.
Dla każdego rozkładu prawdopodobieństwa możemy skonstruować dystrybuantę (CDF, ang. cummulative distribution function). Mówi ona, jakie jest prawdopodobieństwo, że jakaś zmienna przyjmie wartość mniejszą lub równą danej liczbie. Koduje ona wszystkie informacje o rozważanym rozkładzie.
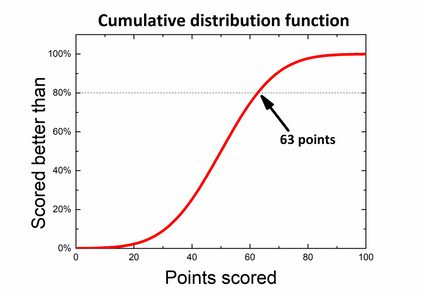
Załóżmy, że bierzesz udział w quizie z wiedzy ogólnej. Konkurs składa się ze 100 pytań, a za poprawną odpowiedź otrzymuje się 1 punkt, podczas gdy za błędną nie przyznaje się punktów. Wiele osób ukończyło już quiz, a z wyników możemy uzyskać rozkład prawdopodobieństwa. Zasady mówią, że tylko 20% najlepszych uczestników otrzymuje nagrody, więc zastanawiasz się, jak dobry wynik musisz uzyskać, aby być wśród zwycięzców. Jeśli spojrzysz na wykres, możesz spróbować podzielić go tak, aby 80% pola pod krzywą gęstości znajdowało się po lewej stronie wartości zadającej podział, a 20% po prawej stronie.
Łatwiejsze jest znalezienie tego podziału przy użyciu dystrybuanty — wystarczy znaleźć wartość 80% na osi pionowej i odpowiadającą jej liczbę punktów na osi poziomej bez obliczania czegokolwiek!
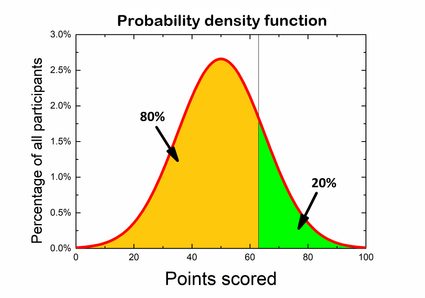
Prawdopodobieństwo teoretyczne a eksperymentalne
Prawie każdy opisany powyżej przykład opisuje prawdopodobieństwo teoretyczne. Pojawia się więc pytanie: jaka jest różnica między prawdopodobieństwem teoretycznym a eksperymentalnym (znanym również jako empiryczne)? Formalna definicja prawdopodobieństwa teoretycznego to stosunek liczby korzystnych wyników do liczby wszystkich możliwych wyników. Opiera się na danych, logicznym rozumowaniu i mówi nam, czego powinniśmy oczekiwać od eksperymentu.
Spójrzmy jeszcze raz na woreczki z kolorowymi kulkami. W sumie są tam 42 kulki, a 18 z nich jest pomarańczowych. Gra polega na wybraniu losowej kulki z woreczka i odłożeniu jej z powrotem, więc w środku zawsze znajdują się 42 kulki. Stosując definicję prawdopodobieństwa, możemy szybko oszacować je jako 18/42, lub, upraszczając ułamek, 3/7. Oznacza to, że jeśli wybierzemy losowo 14 kulek, powinno się nam trafić 6 pomarańczowych.
Z drugiej strony, prawdopodobieństwo eksperymentalne mówi nam co się stało, gdy faktycznie przeprowadzono eksperyment zamiast tego, co powinno się było wydarzyć. Jest ono oparte na stosunku liczby prób zakończonych sukcesem do liczby wszystkich prób. Pozostańmy przy naszym przykładzie — wybierz losową kulkę z woreczka i powtórz procedurę jeszcze 13 razy. Załóżmy, że otrzymasz 8 pomarańczowych kulek w 14 próbach. Wynik ten oznacza, że empiryczne prawdopodobieństwo wynosi 8/14 lub 4/7.
Jak widać, wynik różni się od teoretycznego. Nie ma w tym nic dziwnego, powtarzając tę grę wiele razy, czasami wybierzemy więcej, czasami mniej, a czasami dokładnie 6 pomarańczowych kulek, czyli liczbę przewidywaną teoretycznie. Ważne jest to, że jeśli będziemy brać pod uwagę wyniki wielu gier, prawdopodobieństwo empiryczne będzie stawało się coraz bliższe prawdopodobieństwa teoretycznego. Jeśli tak nie jest, możemy podejrzewać, że wybieranie piłek z worka nie jest całkowicie losowe, np. piłki w różnych kolorach mają nierówne rozmiary, co wpływa na to, które kulki wyciągamy.
Prawdopodobieństwo i statystyka
Zarówno statystyka, jak i prawdopodobieństwo są gałęziami matematyki i zajmują się występowaniem zdarzeń. Jednak każdy powinien być świadomy różnic, które sprawiają, że są to dwa odrębne obszary nauki.
-
Prawdopodobieństwo jest teoretyczną dziedziną matematyki i bada konsekwencje matematycznych definicji i twierdzeń. Statystyka zaś jest zazwyczaj praktycznym zastosowaniem matematyki w codziennych sytuacjach i próbuje przypisać sens i zrozumienie obserwacji w prawdziwym świecie.
-
Prawdopodobieństwo przewiduje możliwość wystąpienia zdarzeń, podczas gdy statystyka jest zasadniczo analizą częstotliwości występowania zdarzeń w przeszłości i tworzy model oparty na zdobytej wiedzy.
-
Wyobraźmy sobie probabilistę grającego w grę karcianą, która polega na wyborze losowej karty z całej talii i tylko piki mają pewną szansę na zwycięstwo. Zakładając, że talia jest kompletna, a wybór jest całkowicie losowy i sprawiedliwy, nasz probabilista wnioskuje, że prawdopodobieństwo wyciągnięcia pika jest równe
¼i może obstawić zakład. -
Statystyk będzie najpierw przez chwilę obserwował grę, aby sprawdzić, czy faktycznie jest ona uczciwa. Po zweryfikowaniu (z akceptowalnym przybliżeniem), że gra jest warta grania, zapyta probabilistę, co powinien zrobić, aby wygrać jak najwięcej.
Statystyka w obrębie dużej grupy osób: próbkowanie probabilistyczne
Czy nie dziwiło cię nigdy, że niektóre sondaże preferencji wyborczych są tak precyzyjne w porównaniu z ostatecznymi wynikami wyborów, nawet jeśli liczba zapytanych osób jest znacznie niższa niż całkowita liczba wyborców? Stoi za tym tzn. próbkowanie probabilistyczne.
Podstawowym założeniem tego próbkowania jest to, że ochotnicy są wybierani losowo z wcześniej określonym prawdopodobieństwem. Możemy rozróżnić wiele różnych metod próbkowania:
- Prosty losowy dobór próby
- Losowy dobór klastrowy
- Systematyczny dobór próby
- Dobór, w którym prawdopodobieństwo jest proporcjonalne do wielkości próby
- Stratyfikowany losowy dobór próby
- Minimaksowy dobór próby
- Dobór przypadkowy
- Dobór kwotowy
- Dobór dobrowolny
- Dobór panelowy
- Dobór metodą śnieżnej kuli
- Dobór metodą przecięcia linii
- Dobór teoretyczny
Każda z tych metod ma swoje zalety i wady, ale większość z nich działa na zadowalającym poziomie. Istotnymi zaletami próbkowania probabilistycznego są oszczędność czasu i efektywność kosztowa, ponieważ badana jest ograniczona liczba osób. Prostota tej procedury nie wymaga żadnej wiedzy specjalistycznej i może być przeprowadzona bez większych przygotowań.
Praktyczne zastosowanie teorii prawdopodobieństwa
Jak pewnie udało ci się już zorientować, istnieje wiele obszarów, w których teoria prawdopodobieństwa ma zastosowanie. Większość z nich to gry z wysokim czynnikiem losowym, takie jak rzucanie kośćmi lub wybieranie jednej kolorowej kuli spośród kul o 10 różnych kolorach, lub też wiele gier karcianych. Loterie i gry hazardowe to rodzaje gier, które w dużym stopniu wykorzystują koncepcję prawdopodobieństwa i powszechny brak wiedzy na jego temat. Oczywiście od czasu do czasu ktoś wygrywa, ale prawdopodobieństwo, że tą osobą będziesz ty, jest niezwykle małe.
Teoria prawdopodobieństwa jest również wykorzystywana do rozwiązywania wielu innych rodzajów problemów. Zwłaszcza gdy mówimy o inwestycjach, warto wziąć pod uwagę ryzyko, aby wybrać najbardziej odpowiednią opcję.
Nasz kalkulator białych Świąt 🇺🇸 wykorzystuje dane historyczne i wiedzę o prawdopodobieństwie, aby przewidzieć wystąpienie pokrywy śnieżnej w różnych miastach w okresie Świąt Bożego Narodzenia.
FAQs
Jak obliczyć prawdopodobieństwo wystąpienia A i B?
Jeśli A i B są zdarzeniami niezależnymi, to wystarczy pomnożyć ich prawdopodobieństwa, aby uzyskać prawdopodobieństwo wystąpienia zarówno A, jak i B. Na przykład, jeśli prawdopodobieństwo wystąpienia A wynosi 20% (0,2), a prawdopodobieństwo wystąpienia B wynosi 30% (0,3), to prawdopodobieństwo wystąpienia obu zdarzeń wynosi 0,2 ∙ 0,3 = 0,06 = 6%.
Jak obliczyć prawdopodobieństwo warunkowe?
Aby obliczyć warunkowe prawdopodobieństwo A pod warunkiem B:
- Wyznacz prawdopodobieństwo B, tj. P(B).
- Wyznacz prawdopodobieństwo A i B, tj. P(A∩B).
- Podziel wynik z kroku 2 przez wynik z kroku 1.
- To wszystko! Wzór wygląda następująco: P(A|B) = P(A∩B) / P(B).
Jakie jest prawdopodobieństwo wyrzucenia 2 szóstek?
Jeśli używasz uczciwych kości, to prawdopodobieństwo wyrzucenia dwóch szóstek wyniesie 1/6 ∙ 1/6 = 1/36 = 0,027 = 2,7%. Oznacza to, że potrzeba 36 rzutów kośćmi, aby oczekiwać wyrzucenia dwóch szóstek przynajmniej raz, choć oczywiście nie ma gwarancji, że to się uda.
Jak przeliczyć szansę na procenty?
Przelicz szansę na liczbę dziesiętną, a następnie pomnóż przez 100. Na przykład, jeśli szansa wynosi 1 do 9, to przeliczamy 1/9 = 0,1111 w postaci dziesiętnej. Następnie mnożymy przez 100, aby otrzymać 11,11%.