Gleitkommazahl Rechner

Der Gleitkommazahl-Rechner soll dir helfen, den IEEE754-Standard für das floating-point-Format zu verstehen. Er funktioniert als Umrechner für Gleitkommazahlen — er wandelt 32-Bit-Gleitkommazahlen und 64-Bit-Gleitkommazahlen von binären Darstellungen in reale Dezimalzahlen um und umgekehrt.

Bevor wir uns mit den Bits und Bytes der Zahlenformate float32 und float64 beschäftigen, wollen wir lernen, wie der Gleitkommazahl-Rechner funktioniert. Befolge einfach diese einfachen Schritte:

1. Wenn du die Binärkodierung einer Gleitkommazahl in die von ihr repräsentierte Dezimalzahl umwandeln möchtest, wähle oben im Rechner die Option Gleitkomma in Zahl. Dann:

   • Wähle die verwendete Genauigkeit. Damit legst du fest, wie deine binäre Darstellung interpretiert wird.

   • Gib die binären Ziffern der Gleitkommazahl ein. Du kannst das Vorzeichen, die Potenz und den Dezimalteil getrennt eingeben oder die gesamte Bitfolge auf einmal — wähle dies im Dropdown-Menü Biteingabemethode.

   • Der Wert, der in deinem Float gespeichert ist, wird unten im Rechner angezeigt.

2. Wenn du einen Wert in seine Gleitkommadarstellung umwandeln möchtest, wähle oben im Rechner Zahl in Gleitkomma. Dann:

   • Gib deine Zahl in das Feld darunter ein.

   • Die IEEE754-Gleitkommadarstellung in Binär- und Hexadezimaldarstellung von einfach- und doppeltgenauen Gleitkommazahlen wird unten angezeigt.

   • Der Gleitkommazahl-Rechner zeigt dir auch den wirklich gespeicherten Wert an, da das Gleitkomma-Format einen Präzisionsverlust aufweist. Der Fehler, der durch den Verlust der Genauigkeit entsteht, wird ebenfalls angezeigt.

In der Informatik ist eine Gleitkommazahl (Englisch: floating-point) ein Datenformat, das verwendet wird, um Dezimalzahlen in einer digitalen Maschine zu speichern. Eine Gleitkommazahl oder Fließkommazahl wird durch eine Reihe von Bits (1 und 0) dargestellt. Computer führen mathematische Operationen direkt mit diesen Bits durch, anstatt die Berechnungen wie ein Mensch durchzuführen. Wenn ein Mensch die Gleitkommazahl lesen möchte, müssen die Bits zuerst durch eine komplexe Formel in das Dezimalsystem umgewandelt werden.

Der IEEE754-Standard (1985 vom Institute of Electrical and Electronics Engineers eingeführt) standardisiert das Floating-Point-Format und legt fest, wie das Format für mathematische und andere Aufgaben verwendet werden kann. Es wurde von vielen Hardware- und Softwareentwicklern übernommen und ist der de facto Standard für die Darstellung von Gleitkommazahlen in Computern. Wenn jemand im Zusammenhang mit Computern von „Gleitkommazahlen“ spricht, meint er in der Regel das Datenformat IEEE754.

Das bekannteste IEEE754-Gleitkommaformat (Einzelpräzision oder „32-Bit“) wird in fast allen modernen Computeranwendungen verwendet. Das Format ist sehr flexibel: mit float32 können Zahlen von 1,4∙10^-45 bis zu 3,4∙10³⁸ (sowohl positive als auch negative) kodiert werden.

Neben der einfachen Genauigkeit kodiert der IEEE754-Standard auch doppelte Genauigkeit („64-Bit“ oder float64), die Zahlen von 5∙10^-324 bis 1,7∙10³⁰⁸ speichern kann. Zu den weniger gebräuchlichen IEEE754-Formaten gehören:

• Halbpräzision („16-Bit“);
• Vierfache Genauigkeit („128-Bit“); und
• Achtfache-Genauigkeit („256-Bit“).

Eine Gleitkommazahl ist jedoch nicht nur eine Zahl, die in das binäre Zahlensystem umgewandelt wird — sie ist viel komplizierter als das! Hier erfährst du, wie der IEEE754 Floating-Point-Standard funktioniert.

Jede binäre Gleitkommadarstellung besteht aus drei Bitsegmenten: Vorzeichen, Potenz und Dezimalteil.

• Das Vorzeichen (S) steht für positiv oder negativ;
• Der Exponent (E) erhöht 2 mit einer Potenz, um die Zahl zu skalieren; und
• Der Dezimalteil (F) bestimmt die genauen Ziffern der Zahl.

Die Länge der Segmente und die genaue Formel, die auf S, E und F angewendet wird, um die Zahl zu erzeugen, hängen von der Genauigkeit des Formats ab.

Bei der Speicherung im Speicher werden $S$, $E$ und $F$ aneinandergereiht, um die vollständige binäre Darstellung der Gleitkommazahl zu erhalten. Im Computerspeicher könnte das folgendermaßen aussehen:

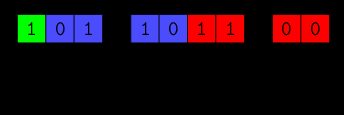
Mit diesen Bits arbeitet der Computer, wenn er arithmetische und andere Operationen durchführt. Der Computer sieht eine Zahl nie als Dezimalziffer — er sieht und arbeitet nur mit diesen Bits.

Schauen wir uns die beiden am häufigsten verwendeten Gleitkommaformate an: float32 und float64.

float32 ist das gebräuchlichste der IEEE754-Formate. Wie der Begriff „32-Bit-Gleitkommazahl“ schon sagt, ist die zugrunde liegende Binärdarstellung 32 Bits lang. Diese sind wie folgt unterteilt:

• 1 Bit für das Vorzeichen ($S$);
• 8 Bits für den Exponenten ($E$); und
• 23 Bits für den Dezimalteil ($F$).

Im Speicher sehen die Bits wie folgt aus:

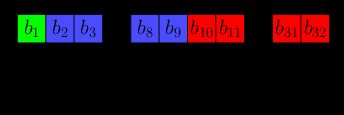
Wir können sie als binäre Zeichenfolge umschreiben:

Der reale Wert, den dieser 32-Bit-Gleitkommazahl speichert, kann wie folgt berechnet werden:

wobei:

• $127$ — wird als Exponentenverzerrung bezeichnet und ist für das einstellige Format typisch;
• $x_2$ — das $x$ muss so interpretiert werden, als ob es zur Basis 2 oder binär wäre; und
• $(1,\!b_{10}...b_{32})_2$ — die binären Bits $b_{10}$ bis $b_{32}$ werden als Dezimalteil von $1$ verwendet, um eine binäre Dezimalzahl zu bilden. In unserem Binär in Dezimal Umrechner 🇺🇸 findest du Hilfe dazu.

Wir können die Formel besser umschreiben, indem wir $S$, $E$ und $F$ verwenden:

wobei

• $S = b_1$;
• $E = (b_2\ ...\ b_9)_2$; und
• $F = (b_{10}\ ...\ b_{32})_2$.

Damit Gleitkommaformate wirklich kleine Zahlen mit hoher Genauigkeit speichern können, aktivieren $E=0$ und $F>0$ eine eigene Formel. Für float32 lautet diese Formel:

Zahlen, die mit dieser Formel erzeugt werden, nennt man „subnormale Zahlen“, während „normale Zahlen“** mit der vorherigen Formel erzeugt werden.

Es gibt andere Sonderfälle, die durch spezifische Werte für $E$ und $F$ verschlüsselt werden:

$\text{NaN}$ bedeutet „keine Zahl“ (not a number), was zurückgegeben wird, wenn du durch null teilst oder unmögliche Mathematik mit Unendlichkeit durchführst. Für die Fälle $\pm 0$ und $\pm \infty$ bestimmt das Vorzeichenbit, ob die Zahl positiv oder negativ ist. Und ja, die negative Null gibt es wirklich!

Ein Beispiel

Wir wandeln die binäre Gleitkommadarstellung 01000001110111100000000000000000 in die reale Zahl, die sie darstellt, um.

1. Zuerst unterteilen wir sie in $S$, $E$ und $F$:

   • $S = 0_2 = 0$

   • $E = 10000011_2 = 131$

   • $F = 10111100000000000000000_2$

2. Da $0<E<255$, verwenden wir die normale Zahlenformel:

   $(-1)^S \cdot 2^{E-127} \cdot (1,\!F)_2$

   • $(-1)^S = 1$ (also ist die Zahl positiv!)

   • $2^{E-127} = 2^{4} = 16$

   • $(1,\!F)_2 = 1,\!101111_2 = 1,\!734375$

3. Kombiniere die drei Multiplikatoren:

   $1 \cdot 16 \cdot 1,\!734375 = \textbf{27,\!75}$

Möchtest du es selbst sehen? Probiere diesen Wert in unserem Gleitkomma-Rechner aus, um ihn in Aktion zu sehen!

Beachte, dass $01000001110111100000000000000000_2$ bei der direkten Umwandlung von Binär- in Dezimalzahlen nicht $27,\!75$, sondern $1\hspace{0.5mm}105\hspace{0.5mm}068\hspace{0.5mm}032$ ist. Ein ziemlicher Unterschied, findest du nicht auch?

Die innere Funktionsweise des Datentyps float64 ist weitgehend identisch mit der von float32. Die einzigen Unterschiede sind:

• Die Längen der Exponenten- und Dezimalsegmente der Binärdarstellung — bei 64-Bit-Gleitkommazahlen nimmt $E$ 11 Bits und $F$ 52 Bits in Anspruch.
• Die Verzerrung des Exponenten — in 64-Bit-Gleitkommazahlen beträgt sie 1023 (in 32-Bit-Gleitkommazahlen 127).

Die Formeln für die Rekonstruktion von 64-Bit-Normal- und Subnormal-Gleitkommazahlen lauten daher wie folgt:

und

Durch die zusätzlichen Bits für den Exponenten und die Nachkommastellen im Vergleich zu float32 kann float64 viel größere Zahlen und mit viel höherer Genauigkeit speichern.

Um eine Dezimalzahl in eine Gleitkommadarstellung umzuwandeln, befolge diese Schritte:

1. Wandle die gesamte Zahl in die binäre Schreibweise um und normiere sie dann, d. h. schreibe sie in wissenschaftlicher Notation zur Basis 2 auf.
2. Kürze die Dezimalzahl nach dem Komma auf die erlaubte Dezimallänge.
3. Extrahiere das Vorzeichen, den Exponenten und die Dezimalteile.

Genauere Anweisungen findest du im IEEE754-Standard.

Ein Beispiel

Wir wandeln $27,\!75$ zurück in seine Gleitkommadarstellung um.

1. Unser ganzzahliger Teil ist $27$, der im Binärformat $11011_2$ ist. Unser Dezimalteil ist $0,\!75$. Wandeln wir ihn in eine binäre Dezimalzahl um:

   • $0,\!75 \cdot 2 = 1,\!50 = \textbf{1} + 0,\!5$

   • $0,\!5 \cdot 2 = 1,\!00 = \textbf{1} + 0$

   Also $0,\!75 = 0,\!11_2$, und dann $27,\!75 = 11011,\!11_2$. Um sie zu normalisieren, schreiben wir sie um als:

2. Die Ziffern nach dem Komma haben bereits eine geeignete Länge — für float32 wären wir auf 23 Bits beschränkt, aber wir haben nur fünf.

Aus der normalisierten Umwandlung können wir erschließen, dass:

• $S = 0$, da die Zahl positiv ist;
• $E = \textcolor{blue}{4}+127 = 10000011_2$ (wir fügen $127$ hinzu, weil $E-127$ $\textcolor{blue}{4}$ sein muss); und
• $F = \textcolor{red}{101111}00000000000000000$ (Nullen werden auf der rechten Seite aufgefüllt, weil es sich um Nachkommastellen und nicht um eine ganze Zahl handelt).

Unsere Gleitkomma-Darstellung ist also $0\textcolor{blue}{10000011}\textcolor{red}{101111}00000000000000000$.

Du kannst dieses Ergebnis mit unserem Gleitkommazahl-Rechner überprüfen!

Gleitkommazahlen können nicht alle möglichen Zahlen mit vollständiger Genauigkeit darstellen. Das macht intuitiv Sinn für ausreichend große Zahlen und für Zahlen mit einer unendlichen Anzahl von Dezimalstellen, wie Pi ($\pi$) und die Eulersche Zahl ($e$). Aber wusstest du, dass Computer einen so einfachen Wert wie $0,\!1$ nicht mit 100%-iger Genauigkeit speichern können? Gehen wir dieser Behauptung auf den Grund!

Wenn du einen Computer bittest, $0,\!1$ als float32 zu speichern, wird er diesen binären String speichern:

00111101110011001100110011001101.

Wenn wir das mit den oben gelernten Gleitkomma-Formeln zurück in Dezimalzahlen umrechnen, erhalten wir folgendes Ergebnis:

• $S = 0$
• $E = 01111011_2 = 123$
• $F = 10011001100110011001101_2$

Das ist ein kleines bisschen mehr als $0,\!1$! Der Fehler (wie weit der gespeicherte Gleitkommawert von dem „richtigen” Wert von $0,\!1$ entfernt ist) beträgt $1,\!49 \cdot 10^{-9}$.

Lass uns versuchen, diesen Fehler zu korrigieren und die kleinstmögliche Änderung vorzunehmen. Unsere gespeicherte Zahl ist ein bisschen zu groß, also ändern wir das letzte Bit von $1$ zu $0$, um unseren Float ein bisschen kleiner zu machen. Wir konvertieren jetzt:

00111101110011001100110011001100

• $S = 0$
• $E = 01111011_2 = 123$
• $F = 10011001100110011001100_2$

Und wir haben unser Ziel von $0,\!1$ wieder verfehlt! Diesmal ist der Fehler ein bisschen größer ($5,\!96\cdot 10^{-9}$). Die erste binäre Zeichenkette, die auf 1 endete, war sogar noch korrekter als diese!

Du denkst vielleicht: „Was wäre, wenn wir mehr Bits verwenden würden?“ Wenn wir das Gleiche mit dem Format float64 machen würden, hätten wir das gleiche Problem, wenn auch weniger gravierend. $0,\!1$, umgerechnet in eine 64-Bit-Gleitkommazahl und zurück in Dezimalzahlen, ist $0,\!100000000000000006$ und der Fehler hier ist $5,\!55 \cdot 10^{-18}$. Das ist die höhere Genauigkeit von float64 in Aktion, aber der Fehler ist immer noch nicht $0$ — die Umwandlung ist immer noch nicht verlustfrei.

Das ist leider der Nachteil des Gleitkommaformats — es ist nicht zu 100% genau. Kleine Informationen gehen verloren, und wenn sie nicht berücksichtigt werden, können sie verheerende Folgen haben. Die einzigen Zahlen, die perfekt und ohne Verluste als Gleitkommazahl gespeichert werden können, sind Potenzen von 2, die durch ganze Zahlen skaliert werden, weil das Format Zahlen so speichert. Alle anderen Zahlen werden einfach nur angenähert, wenn sie als Gleitkommazahl gespeichert werden. Aber es ist immer noch das Beste, was wir haben!

Der IEEE754-Standard für Gleitkommaformate ermöglicht eine effiziente Speicherung und Verarbeitung von Zahlen in Computern.

• Aus der Hardware-Perspektive können dank der Spezifikationen des IEEE754-Standards viele Vereinfachungen von Floating-Point-Operationen vorgenommen werden, um die Arithmetik deutlich zu beschleunigen.

• Für Software sind Gleitkommazahlen sehr präzise und verlieren in der Regel ein paar Millionstel (wenn nicht weniger) pro Operation, was hochpräzise wissenschaftliche und technische Anwendungen ermöglicht.

Die Gleitkommadarstellung von 12,25 ist 01000001010001000000000000000000. Das Vorzeichen ist 0, der Exponent ist 10000010₂ = 130, und der Dezimalteil ist 100010...0. Umgerechnet in Dezimalzahlen erhalten wir:

(-1)⁰ ∙ 2^(130-127) ∙ (1,10001)₂
= 1 ∙ 2³ ∙ 1,53125
= 12,25