Gewinderechner

Dieser Gewinderechner hilft dir, die verschiedenen Gewindegrößen von Schrauben und Muttern nach metrischen ISO-Normen zu ermitteln. In diesem Gewinderechner lernst du:

• Wie du metrische Gewindegrößen bestimmst;
• Wie du metrische Gewindebeschriftungen lesen und verstehen kannst;
• Die Formeln für metrische Außengewinde;
• Die Formeln für metrische Innengewindeabmessungen; und
• Was metrische Gewindeklassen bedeuten.

Beginnen wir damit, zu lernen, was Gewinde sind. 🔩

Gewinde können viele Dinge bedeuten. In diesem Gewinderechner geht es um das Schraubengewinde, das aus Rillen und Stegen besteht, die spiralförmig um einen zylindrischen oder konischen Metallschaft gewickelt sind. Das Spiralmuster des Gewindes wirkt wie eine schräge Ebene, die eine Drehbewegung in eine axiale Bewegung umwandelt und dabei einen mechanischen Vorteil erzielt.

Daher bietet ein Gewinde eine Verriegelungsfunktion, die nur durch eine hohe Scherbeanspruchung zu brechen ist. Diese Art von Gewinde kann ein Außengewinde (wie bei einer Schraube oder einem Bolzen) oder ein Innengewinde (wie in einer Mutter) sein. Wir nennen diese Gewindematerialien Gewindebefestigungsmittel.

Obwohl wir Gewinde auch in anderen Anwendungen wie Flaschenverschlüssen, Glühbirnen, Rohren und Verbindungsstücken und sogar Schneckenrädern sehen können, konzentriert sich dieser Gewinderechner speziell auf metrische Gewinde. Metrische Gewinde haben symmetrische V-förmige Gewinde, die 60º-Winkelrillen bilden, und die unten angegebenen Grundmaße haben:

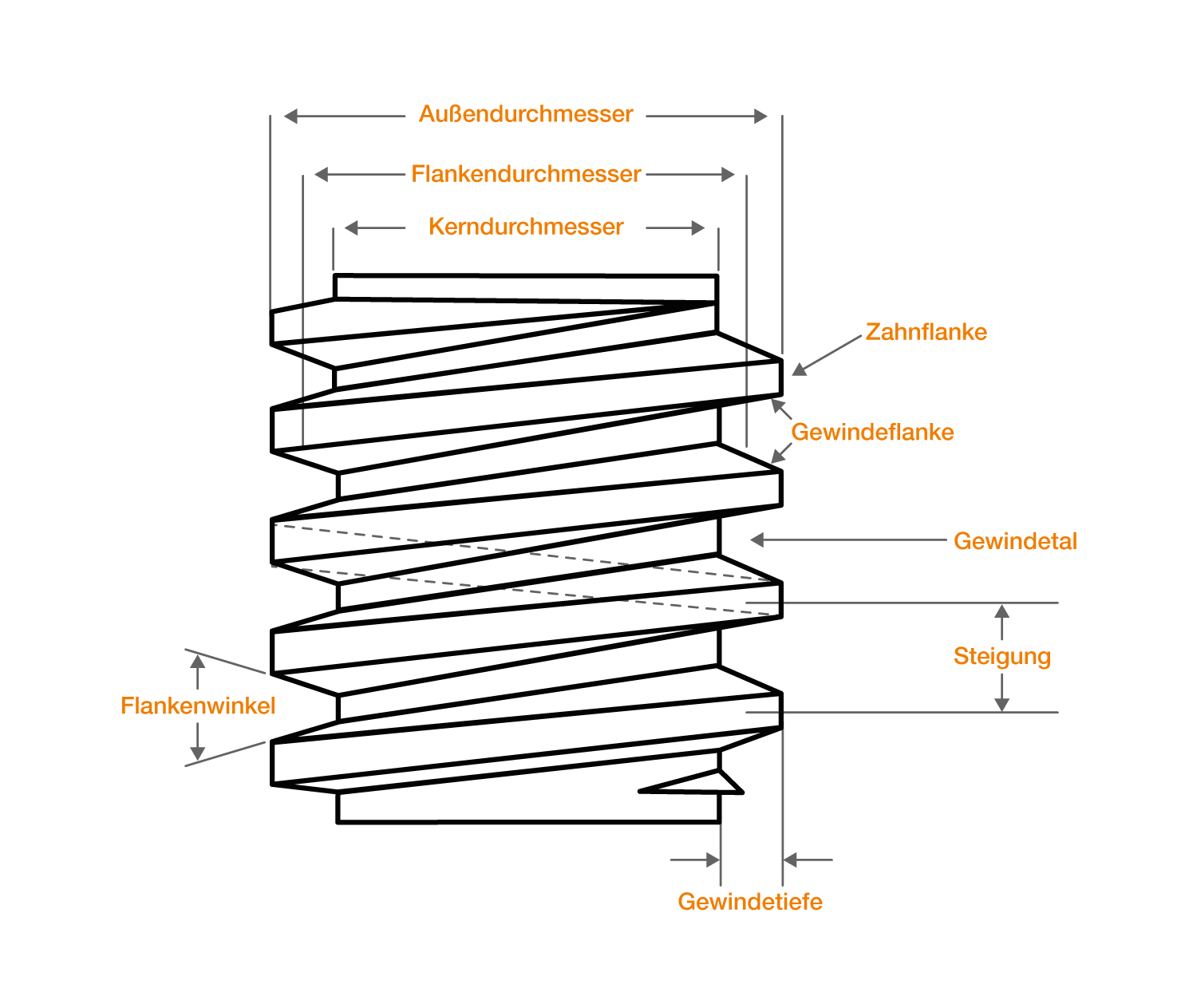
Der Hauptdurchmesser ist der größte Durchmesser eines Außen- oder Innengewindes. Wir nennen diesen Durchmesser auch den Außendurchmesser oder Nenndurchmesser des Gewindes. Der kleine Durchmesser ist dagegen der kleinste Durchmesser eines Außen- oder Innengewindes. Wir nennen ihn auch den Grund- oder Kerndurchmesser des Gewindes.
Zwischen diesen beiden Durchmessern liegt der Flankendurchmesser. Der Flankendurchmesser ist der Durchmesser des Gewindes, bei dem die Dicke des Gewindes und der Abstand zwischen zwei Gewinden gleich groß sind. Wir können den Wert des Flankendurchmessers näherungsweise bestimmen, indem wir den Durchschnitt der Kern- und Nenndurchmesser des Gewindes nehmen. Besuche unseren Teilkreisdurchmesser Rechner 🇺🇸, um mehr darüber zu erfahren.

Die Gewindesteigung ist der Abstand zwischen einem Punkt auf einem Gewinde und dem entsprechenden Punkt auf dem benachbarten Gewinde (z. B. das Maß von Kamm zu Kamm oder von Fuß zu Fuß). Mehr über die Gewindesteigung erfährst du in unserem Gewindesteigung Rechner 🇺🇸.

Um deine metrischen Gewinde zu verstehen, musst du wissen, wie man metrische Gewindebeschriftungen liest. Eine Gewindekennzeichnung ist dasselbe wie das Etikett eines Befestigungselements mit Gewinde, das du in einem Baumarkt siehst. Jede Gewindenorm hat ihre eigene Kennzeichnung, und hier ist ein Beispiel für eine metrische Gewindekennzeichnung:

$\text{M10 × 1 × 25}$

wobei:

• $\text{M}$ für „metrisch” steht und bedeutet, dass das Verbindungselement mit Gewinde dem ISO Metrischer Standard entspricht;
• $10$ in diesem Fall die Zahl, die an den Buchstaben M angehängt ist, für den grundlegenden Nenndurchmesser des Gewindes steht;
• $1$ steht für die Gewindesteigung und
• $25$ ist die Länge des Schafts.

Alle Maße in einem metrischen Gewinde sind in Millimetern angegeben.

Jetzt, wo wir die metrischen Gewindebeschriftungen lesen können, können wir damit beginnen, die verschiedenen Abmessungen unserer Gewinde zu berechnen. Wenn wir wissen, wie wir metrische Gewindegrößen bestimmen können, haben wir eine weitere Möglichkeit, ein Befestigungselement mit Gewinde von einem anderen zu unterscheiden. Als Anhaltspunkt dient uns diese Abbildung:

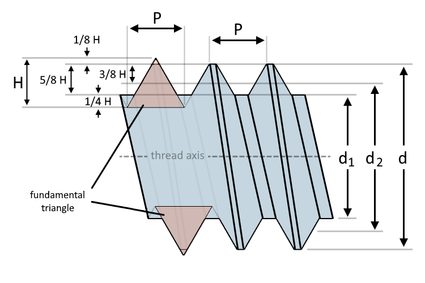
Aus der obigen Abbildung geht hervor, dass wir Bruchteile von H verwenden können, um die verschiedenen metrischen Gewindemaße zu bestimmen, wenn wir den Hauptdurchmesser ($\small{d}$) kennen. Aber was ist H? $\small{H}$ ist die Höhe des Grunddreiecks des Gewindes. Das Grunddreieck ist das projizierte gleichseitige Dreieck, das wir aus dem Querschnitt des Gewindes bilden können. Wir können seine Höhe mit dieser Formel bestimmen:

wobei:

• $P$ – Gewindesteigung.

Wenn wir das obige Diagramm analysieren, können wir die folgenden Gleichungen aufstellen, um die anderen Grunddurchmesser eines Außengewindes zu bestimmen:

• $d_1 = d - 2 \cdot \frac{5}{8} \cdot H$; und

• $d_2 = d - 2 \cdot \frac{3}{8} \cdot H$;

wobei:

• $d$ – Haupt-Nenndurchmesser;
• $H$ – Höhe des Grunddreiecks;
• $d_1$ – Grund-Kerndurchmesser; und
• $d_2$ – Steigungsdurchmesser.

Als Faustregel gilt, dass ein Innengewinde einer bestimmten Größe die gleichen Grunddurchmesser haben sollte wie ein Außengewinde der gleichen Größe. Das bedeutet, dass $d_1 = D_1$, und $d_2 = D_2$, wobei $D_1$ und $D_2$ der Kerndurchmesser des Innengewindes bzw. der Basisdurchmesser der Steigung sind.

Wie wir bereits besprochen haben, stimmen die Grunddurchmesser eines Paares von Außen- und Innengewinden genau überein. In den meisten Fällen jedoch geben wir unseren Gewinden etwas Spielraum für das Zusammenfügen. An dieser Stelle kommen die metrischen Gewindeklassen ins Spiel.

Metrische Gewindeklassen geben den Toleranzgrad und die Toleranzposition eines metrischen Gewindes an. Für jede Toleranzklasse und -position gibt es entsprechende Gleichungen, die uns sagen, wie viel tiefer wir die Gewinde schneiden oder kaltwalzen müssen, um die gewünschten Toleranzen zu erreichen.

Es gibt jedoch Grenzen, wie weit wir von den Grundmaßen der Gewinde abweichen können. Deshalb ist es gut, wenn du die zulässigen Höchst- und Mindestdurchmesser deines Gewindes kennst.

Hier sind die Formeln, die wir verwenden, um diese maximalen und minimalen Durchmesser zu ermitteln:

Für den Nenndurchmesser des Außengewindes (d):

• $d_\text{max} = d + es$
• $d_\text{min} = d + es - T_\text{d}$

Für den Kerndurchmesser des Außengewindes (d₁):

• $d_\text{1max} = d_1 - es - 2 \cdot y$
• $d_\text{1min} = d_1 - es - 2 \cdot z$

Für den Steigungsdurchmesser des Außengewindes (d₂):

• $d_\text{2max} = d_2 + es$
• $d_\text{2min} = d_2 + es - T_\text{d2}$

Für den Nenndurchmesser des Innengewindes (D):

• $D_\text{min} = D + EI$

Für den Kerndurchmesser des Innengewindes (D₁):

• $D_\text{1min} = D_1 + EI$
• $D_\text{1max} = D_1 + EI + T_\text{D1}$

Für den Steigungsdurchmesser des Innengewindes (D₂):

• $D_\text{2min} = D_2 + EI$
• $D_\text{2max} = D_2 + EI + T_\text{D2}$

wobei:

• $es$ und $EI$ – Grundabweichungen, obere bzw. untere Abweichung;
• $T$ – Toleranzen für die entsprechenden Durchmesser (d.h. $T_\text{d2}$ ist die Toleranz für den äußeren Gewindesteigungsdurchmesser ($d_2$)); und
• $y$ und $z$ – Anpassungswerte für den maximalen bzw. minimalen Kerndurchmesser.

Hier sind die Gleichungen, die wir verwenden, um die Grundabweichungen zu ermitteln, je nachdem, welche Toleranzposition die Gewinde haben müssen:

Grundabweichungen für das Außengewinde

• Für die e Position: $\small{es = -(50 + 11 \cdot P) / 1000}$;
• Für die f Position: $\small{es = -(30 + 11 \cdot P) / 1000}$;
• Für die g Position: $\small{es = -(15 + 11 \cdot P) / 1000}$; und
• Für die h Position: $\small{es = 0}$.

Grundlegende Abweichungen für das Innengewinde

• Für die G Position: $\small{EI = (15 + 11 \cdot P) / 1000}$; und
• Für die H Position: $\small{EI = 0}$.

Auf der anderen Seite sind hier die verschiedenen allgemeinen Gleichungen, die wir verwenden, um die Toleranzen basierend auf dem Toleranzgrad des Gewindes zu bestimmen:

Für das Außengewinde

• $\small{T_\text{d}(n) = k \cdot (180 \cdot P^{2/3} - 3,\!15 \times P^{-1/2}) / 1000}$; und
• $\small{T_\text{d2}(n) = k \cdot (90 \cdot P^{0,\!4} \cdot d^{0,\!1}) / 1000}$

Für das Innengewinde

• $\small{T_\text{D1}(n) = k \cdot (433 \cdot P - 190 \cdot P^{1,\!22}) / 1000}$ (für 0,2 mm ≤ P ≤ 0,8 mm);
• $\small{T_\text{D1}(n) = k \cdot (230 \cdot P^{0,\!7}) / 1000}$ (für P ≥ 1,0 mm);
• $\small{T_\text{D2}(n) = k \cdot (90 \cdot P^{0,\!4} \cdot d^{0,\!1}) / 1000}$

In diesen Gleichungen hängt der Wert für $k$ von der Toleranzklasse des Gewindes ab, die durch $n$ angegeben wird. Bei einer Schraube mit einer Toleranzklasse von $n = 6$ für den Hauptdurchmesser sollte $k = 1,\!0$ verwendet werden, um die Gleichung für $T_\text{D1}$ zu lösen. Hier sind die anderen Werte von k in der Tabelle unten:

Du kannst auch sehen, dass wir für den Kerndurchmesser zwei weitere Anpassungsvariablen, $y$ und $z$, in die Gleichung aufgenommen haben. Im Folgenden findest du die Gleichungen, die wir dafür verwenden:

Wir berechnen, dass $R_\text{min}$ gleich $\frac{P}{8}$ ist.

Bei Gewinden mit bestimmten Gewindeklassenangaben können wir deren Codes am Ende der Gewindekennzeichnung hinzufügen. Ein Außengewinde mit der Bezeichnung $\text{M30 × 2 × 40 - 5g6g}$ bedeutet zum Beispiel, dass es eine Toleranzklasse für den Steigungsdurchmesser von $5$ und eine Toleranzklasse für den Nenndurchmesser von $6$ hat, die beide auf eine $\text{g}$ Toleranzposition folgen.

Normalerweise führen wir nur manuelle Berechnungen durch, um die Basisdurchmesser eines Gewindes zu ermitteln. Wie du vielleicht schon festgestellt hast, würde es viele zusätzliche Schritte erfordern, um die Durchmessergrenzen zu bestimmen. Und da kommt unser Rechner für metrische Gewindemaße gerade recht! Hier sind die Schritte, die du bei der Verwendung unseres Tools befolgen kannst:

1. Wähle aus, welche Maße du berechnen möchtest – metrische Außengewindeabmessungen, Innengewindeabmessungen oder beides.
2. Wähle die Gewindesteigung deines Gewindes aus dem Dropdown-Menü.
3. Gib den Nenndurchmesser deines Gewindes ein. Du kannst diesen Wert aus der Gewindeskizze ablesen oder mit einem Messschieber messen.
4. Schließlich wählst du im Abschnitt Toleranzklassen unseres metrischen Gewinderechners die verschiedenen Toleranzklassen und Toleranzpositionen deines Verbindungselements aus, je nachdem, welche dir bekannt sind. Du kannst diese Angaben auch auf deinem Gewindeplan sehen.

Wenn du die oben genannten Schritte ausgeführt hast, siehst du nicht nur die Basisdurchmesser, sondern auch den maximalen und minimalen Durchmesser deines Gewindes.

Du kannst auch auf die Schaltfläche Erweiterter Modus unter dem Rechner klicken, wenn du die verschiedenen Vorabmessungen, die in die Berechnungen einfließen, wie z. B. die Höhe des Grunddreiecks, Abweichungen, Toleranzwerte und Anpassungen wissen möchtest.

Nehmen wir an, wir haben eine Schraube mit einem Grunddurchmesser (d) von 10 mm und einer Gewindesteigung (P) von 1,5 mm. So findest du den Steigungsdurchmesser:

1. Berechne zunächst die Höhe des Grunddreiecks (H) mit H = P ∙ (√3) / 2. H = 1,5 mm ∙ (√3) / 2 = 1,299 mm.
2. Dann ermittle den Steigungsdurchmesser (d₂) mit d₂ = d - 2 ∙ (3 / 8) ∙ H, d₂ = 10 mm - 2 ∙ (3 / 8) ∙ 1,299 mm = 9,026 mm.

Nehmen wir an, wir haben eine Schraube mit einem Nenndurchmesser (d) von 20 mm und einer Gewindesteigung (P) von 2 mm. Um den Kerndurchmesser zu ermitteln:

1. Berechne die Höhe des Grunddreiecks (H) mit H = P ∙ (√3) / 2. H = 2 mm ∙ (√3) / 2 = 1,732 mm.
2. Ermittle den Kerndurchmesser (d₁) mit d₂ = d - 2 ∙ (5 / 8) ∙ H, d₂ = 20 mm - 2 ∙ (5 / 8) ∙ 1,732 mm = 17,835 mm.

Ein M6-Gewinde hat einen grundlegenden Nenndurchmesser von 6 mm. In der Regel wird bei metrischen Gewinden auch die Gewindesteigung angegeben, sodass ein M6 × 1 Gewindebolzen einen Grunddurchmesser von 6 mm und eine Gewindesteigung von 1 mm hat. Wenn du ein Verbindungselement mit Gewinde kaufst, solltest du sowohl den Durchmesser als auch die Gewindesteigung kennen. Ohne eine der beiden Angaben könntest du die falsche Größe kaufen.

Der Nenndurchmesser eines Gewindes ist der Durchmesser, für den ein Gewinde bekannt ist. Wir verwenden den Nenndurchmesser zur allgemeinen Identifizierung von Gewinden. Zum Beispiel hat ein Gewinde mit der Bezeichnung M10 × 1,5 einen Nenndurchmesser von 10 mm. Im Allgemeinen ist der Nenndurchmesser eines Gewindes gleich dem Hauptdurchmesser des Gewindes.