Dreieck Höhe Rechner
Wenn du ein einfaches Werkzeug zur Berechnung der Höhe eines Dreiecks suchst, bist du hier genau richtig. Ganz gleich, ob du nach den Formeln für rechtwinklige, gleichseitige oder gleichschenklige Dreiecke suchst, oder sogar für unregelmäßige Dreiecke – mit diesem Dreieck-Höhe-Rechner bist du auf der sicheren Seite. Er ermöglicht nicht nur die Berechnung der Höhe eines Dreiecks, sondern auch ihrer Seitenlängen, Winkel, Umfänge und Flächeninhalte. Warte nicht länger und probiere ihn aus!
Wenn du dich fragst, wie die Höhe eines Dreiecks berechnet wird (auch ohne bekannten Flächeninhalt), dann scrolle weiter und du wirst eine Antwort darauf finden.
Was ist die Höhe eines Dreiecks?
Jede Seite des Dreiecks kann eine Basis sein, und von jedem Eckpunkt aus kannst du Geraden zeichnen, die senkrecht auf der Geraden der Basis stehen – das sind die Höhen des Dreiecks. Jedes Dreieck hat drei Höhen (rote Geraden in der Abbildung unten).
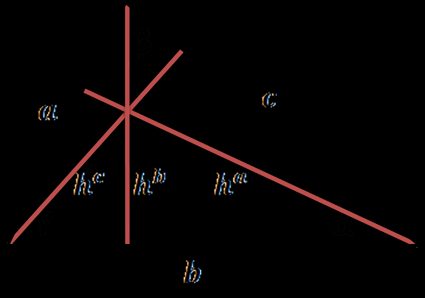
Formeln für die Höhe eines Dreiecks
Was die Berechnung der Höhe eines Dreiecks betrifft, so gibt es durchaus viele Möglichkeiten, die Höhe eines Dreiecks zu berechnen. Am einfachsten ist es, den Flächeninhalt des Dreiecks zu verwenden, aber es gibt noch viele andere Formeln:
-
Gegebene Dreiecksfläche:
Die Gleichung für den Flächeninhalt eines Dreiecks kann nach der Höhe des Dreiecks umgestellt werden:
- ,
wobei:
- – die Grundfläche, und
- – die Höhe ist.
Nach der Höhe umgestellt erhalten wir also:
- .
Aber wie kann man die Höhe eines Dreiecks berechnen, ohne jegliche Angaben zum Flächeninhalt? Zu den bekanntesten Formeln gehören:
-
Gegeben sind die Dreiecksseiten:
Mit dem Satz des Heron kannst du den Flächeninhalt aus den Seitenlängen des Dreiecks berechnen. Wenn du den Flächeninhalt kennst, kannst du die Grundgleichung verwenden, um herauszufinden, wie hoch ein Dreieck ist:
Satz des Heron:
also:
Mehr über diese Gleichung erfährst du in unserem Satz des Heron Rechner 🇺🇸.
-
Gegeben sind zwei Seiten und ein Winkel (SWS)
Verwende die Kongruenzsätze für den Flächeninhalt eines Dreiecks:
(oder oder , abhängig davon, welche Seitenlängen du gegeben hast). Die Höhe berechnet sich also als:
Wenn es sich bei deiner Form um einen speziellen Dreieckstyp handelt, scrolle nach unten, um die Formeln für die Dreieckshöhe zu finden. Vereinfachte Versionen der allgemeinen Gleichungen sind leichter zu merken und zu berechnen.
Höhe eines gleichseitigen Dreiecks
Ein gleichseitiges Dreieck hat drei gleichlange Seiten und alle drei Winkel betragen . Dementsprechend haben auch alle drei Höhen die gleiche Länge:
- , wobei eine Seite des Dreiecks ist.
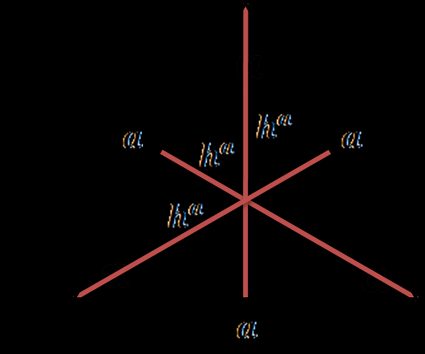
In einem gleichseitigen Dreieck sind die Höhen, die Winkelhalbierenden, die Mittelsenkrechten und die Mediane jeweils gleich groß.
Wenn du dich für die Formeln für den Flächeninhalt und den Umfang interessierst, schaue dir unseren Gleichseitiges Dreieck Rechner an.
Höhe eines gleichschenkligen Dreiecks
Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten. Es gibt zwei verschiedene Höhen eines gleichschenkligen Dreiecks; die Formel für die Höhe vom Schwerpunkt aus lautet:
-
wobei ein Schenkel des Dreiecks und die Basis ist. Die Formel leitet sich aus dem Satz des Pythagoras ab.
-
Die Höhen von den Eckpunkten ausgehend können folgendermaßen berechnet werden:
Flächeninhalt:
Trigonometrie:
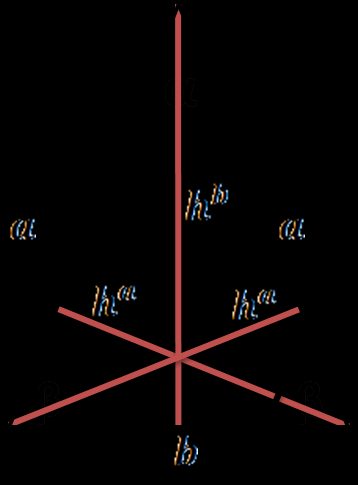
Die Formeln für den Flächeninhalt und den Umfang dieses Dreiecks findest du in unserem Gleichschenkliges Dreieck Rechner.
Höhe eines rechtwinkligen Dreiecks
Ein rechtwinkliges Dreieck ist ein Dreieck, bei dem eines der Winkel beträgt. Zwei Höhen sind leicht zu finden, da die Schenkel senkrecht aufeinander liegen: Wenn der kürzere Schenkel eine Basis ist, dann ist der längere Schenkel die Höhe (und umgekehrt). Die dritte Höhe dieses Dreiecks kann mit der folgenden Formel berechnet werden:

Wenn du dich für die Gleichungen der Fläche und des Umfangs dieses Dreiecks interessierst, schau dir unseren Rechtwinkliges Dreieck Rechner an.
Anwendung des Dreieck-Höhe-Rechners
Jetzt, wo du weißt, wie die Höhe eines Dreiecks mit und ohne den gegebenen Flächeninhalt ermittelt wird, schauen wir uns ein einfaches Beispiel an:
- Wähle den Dreieckstyp. Angenommen, wir möchten die Höhen eines gleichschenkligen Dreiecks berechnen; in diesem Fall bleiben wir bei der Standardoption.
- Gib deine bekannten Werte ein. Das können drei Seiten oder zwei Seiten und ein Winkel sein. Bleiben wir bei der ersten Option: , , .
- Der Dreieck-Höhe-Rechners zeigt alle drei Höhen an: , und . Außerdem zeigte uns der Rechner alle Winkel des Dreiecks, den Flächeninhalt und den Umfang an.
Ist das nicht praktisch?
Wie berechnet man die Höhe eines Dreiecks, wenn alle Seiten gleich lang sind?
Bestimme die Höhe eines gleichseitigen Dreiecks:
- Schreibe die Seitenlänge deines Dreiecks auf.
- Multipliziere sie mit
√3 ≈ 1,73. - Dividiere das Ergebnis durch
2. - Das war's! Das Ergebnis ist die Höhe deines Dreiecks!
Sind alle Höhen eines Dreiecks gleich hoch?
Im Allgemeinen nein, jede Höhe eines Dreiecks kann eine andere Länge haben. Alle drei Höhen sind nur dann gleich lang, wenn es sich um ein gleichseitiges Dreieck handelt, d. h. alle Seiten sind gleich lang (aber nicht gleich den Höhen!).
Wie berechnet man die Höhe eines Dreiecks bei gegebenen Winkeln?
Du kannst die Höhe eines Dreiecks nicht bestimmen, wenn du nur die Winkel des Dreiecks kennst. Das liegt daran, dass es unendlich viele Dreiecke mit diesen Winkeln gibt, und die Längen der Höhen in jedem dieser Dreiecke unterschiedlich sein können!
Wie berechnet man die Höhe eines rechtwinkligen Dreiecks?
Jede der rechtwinkligen Seiten (Schenkel) in einem rechtwinkligen Dreieck ist seine Höhe. Um die dritte Höhe h3 zu berechnen, verwende die Formel für den Flächeninhalt:
½ × Schenkel1 × Schenkel2 = Flächeninhalt = ½ × Hypotenuse × h3.
Daraus folgt:
h3 = Schenkel1 × Schenkel2 / Hypotenuse.
Was ist die kürzeste Höhe eines 3 4 5 Dreiecks?
Die Antwort lautet 2,4. Um zu diesem Ergebnis zu kommen, beachte, dass die Formel für die Fläche Fläche = ½ × 3 × 4 = 6 ist.
Auf der anderen Seite ist Fläche = ½ × Hypotenuse × kürzeste Höhe.
Da Hypotenuse = 5 und Fläche = 6 ist, erhalten wir Kürzeste Höhe = 2 × Fläche / Hypotenuse = 2 × 6 / 5 = 2,4.