Last updated: Apr 19, 2024

Mittlere Änderungsrate Rechner

Q: Ist die mittlere Änderungsrate dasselbe wie die Steigung?

Nicht genau . Die mittlere Änderungsrate gibt an, wie sich eine Funktion im Durchschnitt zwischen zwei Punkten verändert . Andererseits definieren wir die Steigung einer Funktion als die Steigung der Geraden, die die Kurve in einem bestimmten Punkt tangiert . Bei einer linearen Funktion ändert sich jeder Punkt identisch, sodass die mittlere Änderungsrate und die Steigung gleich sind. Read more

Q: Wie hoch ist die mittlere Änderungsrate von y = 2x?

Die mittlere Änderungsrate von y = 2x ist 2 . Da es sich um eine lineare Funktion handelt, ist die mittlere Änderungsrate nur die Steigung der Funktion. In diesem Fall verdoppelt sich bei jeder Änderung der x-Koordinate die y-Koordinate. Read more

Q: Ist die Geschwindigkeit ein Beispiel für eine mittlere Änderungsrate?

Wenn die Geschwindigkeit konstant ist, ja . Die Geschwindigkeit gibt an, wie sich die Position im Verhältnis zur Zeit konstant verändert. Wenn sich ein Objekt also mit konstanter Geschwindigkeit bewegt, gibt die mittlere Änderungsrate der Position Aufschluss darüber, mit welcher Geschwindigkeit es sich fortbewegt. Read more

Table of contents

Was ist die mittlere Änderungsrate? – Definition Formel für die mittlere Änderungsrate Wie berechne ich die mittlere Änderungsrate? – erstes Beispiel Wie berechne ich die mittlere Änderungsrate? – zweites Beispiel FAQs

Der Rechner für die mittlere Änderungsrate soll dir helfen, das einfache Konzept zu verstehen, das sich hinter einem langen, etwas verwirrenden Namen verbirgt. Was ist die Änderungsrate? Allgemein gesagt, zeigt sie das Verhältnis zwischen zwei Faktoren an. Weiter unten findest du eine genauere Definition der mittleren Änderungsrate. Außerdem zeigen und erklären wir dir die Formel für die mittlere Änderungsrate an einigen Anwendungsbeispielen.

Du siehst lieber zu lesen? Mit diesem Video, das wir für dich gemacht haben, lernst du in 90 Sekunden alles, was du brauchst:

Watch this on YouTube

Was ist die mittlere Änderungsrate? – Definition

Alles ist in Bewegung. Veränderung ist unvermeidlich. Angefangen bei der Beschleunigung deines Fahrrads oder Autos bis hin zum Bevölkerungswachstum, vom Blutfluss in deinen Adern bis zur Symbiose deiner Zellen – die Änderungsrate ermöglicht es uns, den mit diesen Veränderungen verbundenen Wert zu ermitteln.

Die mittlere Änderungsrate ist eine Rate, die beschreibt, wie sich eine Zahl im Durchschnitt im Verhältnis zu einer anderen ändert. Bei einer Funktion ist das die Steigung der Gerade zwischen zwei Punkten. Aber verwechsle sie nicht mit der Steigung. Du kannst die mittlere Änderungsrate für jede beliebige Funktion verwenden, nicht nur für lineare Funktionen.

🙋 Wenn du mehr über Steigung erfahren möchtest, besuche den Steigung Rechner.

Formel für die mittlere Änderungsrate

In der folgenden Abbildung haben wir zwei Punkte markiert, damit du besser verstehst, wie man die mittlere Änderungsrate ermittelt.

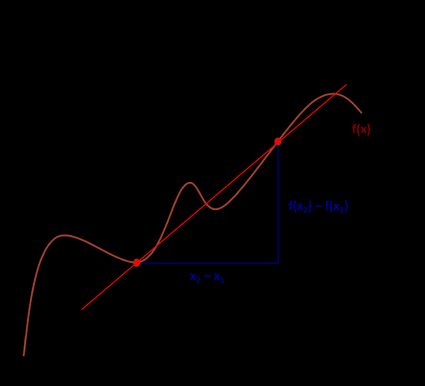
Mittlere Änderungsrate zwischen zwei Punkten einer nichtlinearen Funktion

Die Formel für die mittlere Änderungsrate lautet:

A = [f(x₂) - f(x₁)] / [x₂ - x₁],

wobei:

(x₁, f(x₁)) – die Koordinaten des ersten Punktes sind; und
(x₂, f(x₂)) – die Koordinaten des zweiten Punktes sind.

Ein positiver Wert bedeutet, dass eine Koordinate zunimmt, wenn auch die andere zunimmt. Je mehr du zum Beispiel Fahrrad fährst, desto mehr Kalorien verbrennst du.

Der Wert ist gleich null, wenn sich eine Koordinate ändert, die andere aber nicht. Ein gutes Beispiel dafür wäre, wenn du nicht für deine Prüfungen lernst. Wenn die Zeit abläuft, ändert sich die Menge der zu lernenden Dinge nicht.

Die durchschnittliche Änderungsrate ist negativ, wenn eine Koordinate zunimmt, während die andere abnimmt. Nehmen wir an, du fährst in den Urlaub. Je länger du reist, desto näher kommst du deinem Ziel.

💡 Weitere Möglichkeiten, den Unterschied zwischen zwei Punkten zu beschreiben, findest du im Anstieg Rechner 🇺🇸.

Wie berechne ich die mittlere Änderungsrate? – erstes Beispiel

Berechnen wir die mittlere Änderungsrate der Entfernung (Durchschnittsgeschwindigkeit) eines Zuges, der von Paris nach Rom fährt (1420,6 km). In der folgenden Tabelle siehst du, wie sich die Entfernung im Laufe der Zeit verändert:

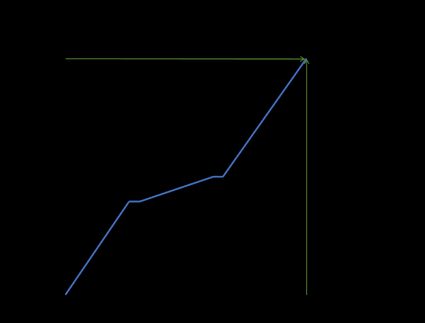
Grafik, die die Veränderung der Entfernung im Laufe der Zeit zeigt

Wie du siehst, war die Geschwindigkeit nicht konstant. Der Zug hat zweimal angehalten und ist zwischen den Stopps deutlich langsamer gefahren. Für die Berechnung der Durchschnittsgeschwindigkeit sind jedoch nur die Veränderung der Entfernung und die Veränderung der Zeit wichtig. Wenn also die Koordinaten des ersten Punktes (0, 0) und die Koordinaten des zweiten Punktes die Entfernung zwischen zwei Städten sind und die Reisezeit (1420,6 h und 12,5 h) beträgt, dann:

A = (1420,6 - 0) / (12,5 - 0) = 113,648 [km/h].

Im Durchschnitt fuhr der Zug also 113,648 Kilometer pro Stunde. Schauen wir uns nun ein etwas mehr auf Mathe-bezogenes Beispiel an.

Wie berechne ich die mittlere Änderungsrate? – zweites Beispiel

Du hast eine Funktion gegeben:

f(x) = x² + 5x - 7

Bestimme die mittlere Änderungsrate über das Intervall [-4, 6].

Finde die Werte deiner Funktion für beide Punkte:

f(x₁) = f(-4) = (-4)² + 5 ∙ (-4) - 7 = -11

f(x₂) = f(6) = 6² + 5 ∙ 6 - 7 = 59
Verwende die Gleichung für die mittlere Änderungsrate:

A = [f(x₂) - f(x₁)] / [x₂ - x₁] = [f(6) - f(-4)] / [6 - (-4)] = [59 - (-11)] / [6 - (-4)] = 70 / 10 = 7

Wenn dir der Rechner für die mittlere Änderungsrate gefallen hat, schau dir auch unsere anderen Tools an, wie zum Beispiel diesen Entfernungsrechner, mit dem du die Entfernung zwischen Punkten oder Geraden ermitteln kannst.

FAQs

Ist die mittlere Änderungsrate dasselbe wie die Steigung?

Nicht genau. Die mittlere Änderungsrate gibt an, wie sich eine Funktion im Durchschnitt zwischen zwei Punkten verändert. Andererseits definieren wir die Steigung einer Funktion als die Steigung der Geraden, die die Kurve in einem bestimmten Punkt tangiert. Bei einer linearen Funktion ändert sich jeder Punkt identisch, sodass die mittlere Änderungsrate und die Steigung gleich sind.

Wie berechnet man die mittlere Änderungsrate einer Funktion?

Um die mittlere Änderungsrate einer Funktion zu ermitteln, gehst du folgendermaßen vor:

Bestimme die Koordinaten (x, y) des Startpunkts. Wir nennen sie (x₀, y₀).
Bestimme die (x, y)-Koordinaten des Endpunkts. Diese lauten (x₁, y₁).
Setze beide in die Formel für die durchschnittliche Änderungsrate (A) ein:

A = (y₁ - y₀)/(x₁ - x₀).

Wie hoch ist die mittlere Änderungsrate von y = 2x?

Die mittlere Änderungsrate von y = 2x ist 2. Da es sich um eine lineare Funktion handelt, ist die mittlere Änderungsrate nur die Steigung der Funktion. In diesem Fall verdoppelt sich bei jeder Änderung der x-Koordinate die y-Koordinate.

Ist die Geschwindigkeit ein Beispiel für eine mittlere Änderungsrate?

Wenn die Geschwindigkeit konstant ist, ja. Die Geschwindigkeit gibt an, wie sich die Position im Verhältnis zur Zeit konstant verändert. Wenn sich ein Objekt also mit konstanter Geschwindigkeit bewegt, gibt die mittlere Änderungsrate der Position Aufschluss darüber, mit welcher Geschwindigkeit es sich fortbewegt.