Raute Flächeninhalt Rechner

Der Raute-Flächeninhalt-Rechner ist ein hervorragendes Hilfsmittel, um den Flächeninhalt einer Raute sowie seinen Umfang und andere Eigenschaften zu bestimmen: Diagonalen, Winkel, Seitenlänge und Höhe.

Schau dir an, auf welche Weise du den Flächeninhalt einer Raute ermitteln kannst: anhand der Diagonalen einer Raute, der Grundseite und der Höhe, der Seiten und eines beliebigen Winkels... Fragst du dich immer noch, wie man den Flächeninhalt einer Raute oder den Umfang einer Raute ermittelt? Schau dir die Formeln für den Flächeninhalt der Raute an oder experimentiere einfach mit dem Tool.

Eine Raute (wie die von den Spielkarten ♢) ist ein einfaches, gleichseitiges Viereck, bei dem alle Seiten gleich sind (siehe Viereck Rechner 🇺🇸).

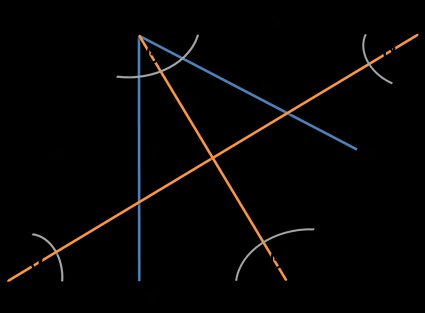
Die grundlegenden Eigenschaften einer Raute sind:

• die beiden Diagonalen einer Raute stehen senkrecht aufeinander und schneiden sich;
• die Diagonalen halbieren gegenüberliegende Winkel; und
• gegenüberliegende Winkel sind gleich groß.

Jede Raute ist ein Parallelogramm und ein Drache. Das könnte dich auch an unserem Parallelogramm Flächeninhalt Rechner und dem Drachen Flächeninhalt Rechner 🇺🇸 interessieren.

Es gibt drei nützliche Formeln für die Berechnung des Flächeninhalts einer Raute:

1. Grundseite und Höhe sind gegeben:

   Flächeninhalt = Grundseite ∙ Höhe

2. Diagonalen der Raute sind gegeben:

   Flächeninhalt = (e ∙ f)/2

3. Seite s und ein beliebiger (!) Winkel sind gegeben:

   Flächeninhalt = s² ∙ sin(Winkel)

Warum können wir in der letzten Formel für den Flächeninhalt der Raute einen beliebigen Winkel verwenden? Weil wir wissen, dass sich zwei benachbarte Winkel ergänzen, und sin(Winkel) = sin(180° - Winkel).

Es gibt noch weitere Varianten dieser Gleichungen (z. B. die Berechnung des Flächeninhalts bei gegebener Höhe und gegebenem Winkel), aber sie sind nur einfache trigonometrische Umformungen dieser drei bekanntesten Formeln für den Flächeninhalt einer Raute.

Den Umfang der Raute zu bestimmen ist trivial, wenn wir die Seitenlänge kennen — er beträgt 4 ∙ a. Aber was ist, wenn wir nur die Diagonalen einer Raute kennen? Schauen wir nach:

1. Wir wissen, dass die Diagonalen senkrecht aufeinander stehen und sich kreuzen. Die Raute ist also nichts anderes als vier kongruente Dreiecke, deren Schenkel e/2 und f/2 sind.

2. Wir müssen nur noch die Hypotenuse des Dreiecks finden. Du kannst dazu den rechtwinkliges Dreieck Rechner oder den Satz des Pythagoras Rechner verwenden.

3. Multipliziere den erhaltenen Wert der Hypotenuse mit 4. Das ist der Umfang deiner Raute!

Du kannst auch diese Formel verwenden:

• Umfang = 4 ∙ √(e/2)² - (f/2)²)

Oder gib einfach die Längen der Diagonalen in den Raute-Flächeninhalt-Rechner ein!

Bist du immer noch unsicher, wie du dieses Tool benutzen sollst? Lass uns sein Potenzial anhand eines einfachen Beispiels demonstrieren:

1. Tippe den ersten vorgegebenen Wert ein, den du hast. Nehmen wir an, dass die Seite = 10 cm ist.

2. Schreibe den zweiten gegebenen Wert. Zum Beispiel, einen Winkel von 30°.

3. Wow! Der Raute-Flächeninhalt-Rechner zeigt alle anderen Werte an — Fläche, Höhe, Umfang, Winkel und Diagonalen. Beeindruckend, nicht wahr?

Unser Tool ist wirklich flexibel — wenn es möglich ist, etwas zu berechnen, wird es das auch tun. Normalerweise reichen zwei vorgegebene Werte aus. Probiere es aus!

Die Antwort ist Ja auf beide Fragen. Jedes Quadrat ist eine Raute, denn für eine Raute ist die einzige notwendige Bedingung, dass alle Seiten gleich lang sein müssen. Wie du weißt, sind bei einem Quadrat alle Seiten gleich lang und alle vier Winkel gleich groß. Somit erfüllt es die Bedingungen für eine Raute.

Genauso ist eine Raute ein Parallelogramm, da jede Form zwei Paare paralleler Seiten haben muss, um ein Parallelogramm zu sein — und die Raute hat sie. Die Raute ist also immer ein Parallelogramm, aber ein Parallelogramm ist nur in einem besonderen Fall eine Raute — nämlich bei einem Parallelogramm mit vier gleich langen Seiten.