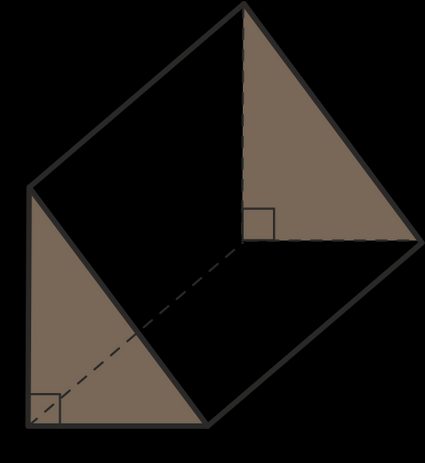
Volumen Dreiecksprisma Rechner

Unser Rechner für das Volumen eines Dreiecksprismas ist ein einfaches Werkzeug, das alle deine Fragen zu dem Thema beantwortet – mit einer der 6 verfügbaren Methoden mit 6 verschiedenen Datensätzen. 📐

Sieh dir den folgenden Artikel an – dort erfährst du nicht nur, wie die Formel für das Volumen eines Dreiecksprismas lautet, sondern wir erklären dir auch die mathematischen Gesetze, die dies ermöglichen.

Bist du bereit? – wir helfen dir, endlich zu verstehen, wie du das Volumen eines Dreiecksprismas bestimmen kannst. 🤓

Ein Dreiecksprisma ist ein Körper, der durch die Umhüllung von zwei parallelen Dreiecken als Ober- und Unterseite gebildet wird. Ein Dreiecksprisma ist ein Polyeder mit Dreiecken als Grundflächen und Rechtecken als Seitenflächen.

Wie berechnet man also das Volumen eines Dreiecksprismas mithilfe unseres Tools? Es ist so einfach, wie es scheint – du bist nur Sekunden von deinem Ergebnis entfernt!

1. Wähle die Art der Dreiecksflächen-Berechnung:

   Überlege dir, was du bereits über das Dreieck im Prisma weißt, und finde heraus, welche Werte gegeben sind:

   • ▲ Basis und Höhe – du kennst bereits die Länge der Basis und die Höhe des Dreiecks;
   • ◣ Rechtwinkliges Dreieck – dein Dreieck hat einen rechten Winkel (90°) zwischen zwei seiner Schenkel. Du kennst die Längen dieser Seiten (diese Option dient als Volumen eines rechtwinkligen Prismas-Rechner);
   • ▲ 3 Seiten – du kennst die Längen aller drei Seiten des Dreiecks;
   • ▲ 2 Seiten + Winkel dazwischen – du kennst die Längen von zwei Seiten und den Wert des Winkels zwischen ihnen;
   • ▲ 2 Winkel + Seite dazwischen – du kennst den Wert von zwei Winkeln des Dreiecks und die Länge der Seite, die zwischen ihnen liegt; oder
   • ▲ Fläche der Dreiecksfläche – die perfekte Option, wenn du schon einen Schritt weiter bist und den Flächeninhalt einer dreieckigen Fläche deines Prismas bereits berechnet hast.

2. Gib alle Daten ein, die du gegeben hast:

   Du kannst aus 11 verschiedenen Einheiten wählen – zögere nicht, sie zu mischen!

3. Deine Ergebnisse sind hier 🎉

Das war doch ganz einfach! Probiere auch unsere weiteren Prismenrechner aus:

🔺 Dreieckig:

• Dreiecksprisma Rechner 🇺🇸; und
• Dreiecksprisma Flächeninhalt Rechner.

♦️ Rechteckig:

• Quader Rechner;
• Rechteckiges Prisma Volumen Rechner; und
• Flächeninhalt eines Quaders Rechner.

Wie wir bereits erwähnt haben, gibt es 6 Möglichkeiten, das Volumen eines Dreiecksprismas mit unserem Rechner zu ermitteln. Lass sie uns alle durchgehen.

1. ▲ Grundfläche und Höhe

   Dies ist die Grundgleichung für das Volumen eines Dreiecksprismas:

   Volumen = 0,5 × Grundfläche × Höhe × Länge,

   wobei:

   • Grundfläche und Höhe die Werte der dreieckigen Fläche des Prismas sind; und
   • Länge die Länge des gesamten Prismas ist, d.h. die Entfernung zwischen zwei Flächen.

2. ◣ Rechtwinkliges Dreieck

   Wahrscheinlich die beliebteste Art des Prismas!

   Die Formel für das rechtwinklige Dreiecksprisma sieht wie folgt aus:

   Volumen = Länge × ((a × b) / 2),

   wobei:

   • a und b die Seiten des Dreiecks sind, die den rechten Winkel berühren; und
   • Länge die Länge des gesamten Prismas ist, d. h. die Entfernung zwischen zwei Flächen.

   Wende den Satz des Pythagoras an, um die Seite c zu berechnen.

3. ▲ 3 Seiten (SSS)

   Volumen = 0,25 × √( (a+b+c) × (-a+b+c) × (a-b+c) × (a+b-c) ) × Länge,

   wobei:

   • √ – ist die Quadratwurzel aller multiplizierten Summen der Dreiecksseiten (x² = y, √y = x);
   • a, b und c – sind die Seiten der Dreiecksfläche; und
   • Länge – die Länge des gesamten Prismas ist, d. h. die Entfernung zwischen zwei Flächen.

4. ▲ 2 Seiten + Winkel dazwischen (SWS)

   Volumen = 0,5 × a × b × sin(γ) × Länge,

   wobei:

   • sin – der Sinus des Winkels γ ist (benutze die Sinustabellen und unseren Sinusgesetz Rechner, um die Grundlage dieser Gleichung zu verstehen);
   • a und b – die Seiten des Dreiecks sind, die den Winkel γ berühren;
   • Winkel γ – dieser Wert muss zwischen 0 und 180 Grad liegen; und
   • Länge – die Länge des gesamten Prismas ist, d. h. die Entfernung zwischen zwei Flächen.

5. ▲ 2 Winkel + Seite zwischen (WSW)

   Volumen = 0,5 × a ×((a × sin(β))/ sin(β + γ))) × sin(γ) × Länge,

   wobei:

   • sin – der Sinus eines bestimmten Winkels ist. Anhand der Sinustabellen, die auf dem Sinusgesetz basieren (wie oben erwähnt) ermittelt;
   • a – die Seite eines Dreiecks ist, die sowohl den γ als auch den β berührt;
   • γ – sein Wert muss zwischen 0 und 180 Grad liegen;
   • β – sein Wert muss zwischen 0 und 180 Grad liegen; und
   • Länge – die Länge des gesamten Prismas ist, d. h. die Entfernung zwischen zwei Flächen.

6. ▲ Flächeninhalt der Dreiecksfläche

   Die beste Lösung ist, wenn du die dreieckige Fläche bereits kennst:

   Volumen = Flächeninhalt der Dreiecksfläche × Länge,

   wobei:

   • Dreiecksgrundfläche – in der Flächeneinheit angegeben wird, z. B. Quadratzentimeter (cm²), Quadratmeter (m²) oder Quadratmeilen (mi²); und
   • Länge – die Länge des gesamten Prismas ist, d. h. die Entfernung zwischen zwei Flächen.