Standardabweichung des Stichprobenmittels Rechner

Die Berechnung der Standardabweichung des Mittelwerts der Stichproben ist eine hervorragende Methode, um zu erkennen, wie der Stichprobenumfang den Fehler unserer Schätzungen beeinflusst.

Wenn die Standardabweichung des Mittelwerts mit einem kritischen Wert wie dem z-Wert oder der t-Statistik multipliziert wird, erhalten wir eine Fehlerspanne, die es uns ermöglicht, ein Konfidenzintervall unserer Vorhersage anzugeben. Die Berechnung der Standardabweichung des Stichprobenmittels zeigt also, wo der Mittelwert der Grundgesamtheit liegen könnte.

Zunächst einmal ist es wichtig, einige Definitionen und Konzepte zu kennen:

• Statistik: eine Punktschätzung oder ein numerisches Merkmal einer Stichprobe (z. B. der Stichprobenmittelwert). Sie unterscheidet sich von einem Parameter, wie dem Mittelwert der Grundgesamtheit.
• Stichprobenverteilung: die Wahrscheinlichkeitsverteilung einer Statistik, die nach dem Zufallsprinzip ermittelt wurde. Mit anderen Worten: Sie ist die Verteilung aller möglichen Werte, die eine Statistik bei gleichem Stichprobenumfang annehmen kann.
• Stichprobenverteilung des Mittelwerts: Dies ist eine Erweiterung des vorherigen Konzepts. Wenn du eine Grundgesamtheit hast, unendlich viele Stichproben der Größe n ziehst und deren Mittelwerte in einem Histogramm aufträgst, erhältst du eine Wahrscheinlichkeitsverteilung. Diese Wahrscheinlichkeitsverteilung nennen wir die Stichprobenverteilung des Mittelwerts, und wie jede andere Verteilung hat sie ihren eigenen Mittelwert und ihre eigene Standardabweichung.

Das folgende Diagramm zeigt, wie man eine Stichprobenverteilung des Mittelwerts erstellt. In Wirklichkeit verwenden wir nicht nur sechs Stichproben, sondern eine fast unendliche Anzahl (z. B. 100 000).

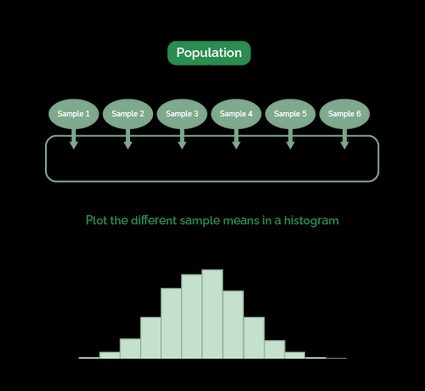
Das heißt, wir können die Standardabweichung des Mittelwerts als Standardabweichung einer Verteilung von Mittelwerten definieren (wie die im letzten Diagramm gezeigte). Außerdem ist der Mittelwert dieser Stichprobenverteilung gleich dem Mittelwert der Grundgesamtheit.

Jetzt, wo du das Konzept kennst, lass uns ansehen, wie du die Standardabweichung des Stichprobenmittelwerts berechnen kannst.

Der Unterschied zwischen einer Stichprobe und einer Stichprobenverteilung ist:

• Stichprobenverteilung: Das ist der Begriff, den wir normalerweise hören. Er bezieht sich auf die Wahrscheinlichkeitsverteilung einer zufällig gezogenen Statistik. Die Stichprobenverteilung des Mittelwerts ist ein Beispiel dafür.
• Probenverteilung: bezeichnet die Verteilung der Beobachtungen innerhalb einer einzigen Stichprobe. Jede Probenverteilung besitzt einen Mittelwert, der zur Bildung der Stichprobenverteilung beiträgt.

Die Formel zur Ermittlung der Standardabweichung des Stichprobenmittelwerts lautet:

σ_X̄ = σ/√n,

wobei:

• σ_X̄ – Standardabweichung des Stichprobenmittelwerts;
• σ – Standardabweichung der Grundgesamtheit; und
• n – Stichprobenumfang.

Wir haben bereits gesagt, dass wir, wenn wir den Mittelwert der Stichprobenverteilung (μ_X̄) kennen, auch den Mittelwert der Grundgesamtheit (μ) kennen, da beide gleich sind (μ_X̄ = μ). In der Praxis kennen wir μ_X̄ nie, aber wir können ihn anhand des Stichprobenmittelwerts (X̄) schätzen.

σ_X̄ gibt an, wie X̄ sich μ annähert. Je kleiner σ_X̄ ist, desto näher kann μ an unserer Schätzung liegen. Da σ konstant ist, ist eine Erhöhung des Stichprobenumfangs die einzige Möglichkeit, σ_X̄ zu verkleinern. Daher ist die Erhöhung von n eine Möglichkeit, den Stichprobenfehler 🇺🇸 unserer Schätzungen zu verringern.

Wir wissen, dass der Mittelwert und die Standardabweichung der Körpergröße der erwachsenen amerikanischen weiblichen Bevölkerung etwa μ = 161,3 cm und σ = 7,1 cm betragen. Nehmen wir nun an, du nimmst Zufallsstichproben von 100 Frauen und ermittelst jedes Mal ihre durchschnittliche Körpergröße. Wie groß ist die Standardabweichung des Stichprobenmittelwerts?

Um die Antwort zu erfahren, befolge diese Schritte:

1. Gib 7,1 in das Feld für die Standardabweichung der Grundgesamtheit ein.
2. Gib 100 in das Feld für den Stichprobenumfang ein.
3. Das war's. Die Antwort ist 0,71. Die Standardabweichung der Stichprobenverteilungen der Mittelwerte n = 100 ist also 0,71.

Du kannst die Ergebnisse mithilfe der Formel überprüfen: $σ_{\bar X} = \frac{σ}{\sqrt{n}} = \frac{7,\!1}{\sqrt{100}} = 0,\!71$.