Última actualización: 30 de Oct. de 2024

Calculadora del volumen de un tanque

Q: ¿Cómo calcular el volumen de un depósito de agua?

Puedes probar con la calculadora de volumen de depósitos de la herramienta Omni Calculator o hacer lo siguiente: Obtén el radio interior y la altura del depósito . Eleva al cuadrado el radio y luego multiplica por pi (3.14159...). Enhorabuena, ya tienes el área del depósito de agua. Multiplica el resultado por la altura, y obtendrás el volumen del depósito .

Q: ¿Cómo calcular la cilindrada de mi motor?

Los expertos en automóviles lo llaman cilindrada del motor, y puedes calcularla del siguiente modo: Obtén el volumen de uno de los cilindros de tu motor. Puedes probar con la calculadora de volumen del depósito de la herramienta Omni Calculator u obtener el radio y la altura del cilindro (carrera del pistón del motor). Eleva al cuadrado el radio, multiplica por pi (3.14159...), y luego por la carrera del pistón. Multiplica el volumen de un cilindro por el número de cilindros de tu motor, y obtendrás la cilindrada.

Q: ¿Cuánto tiempo puede durar el agua almacenada en un depósito?

Dependerá de la cantidad de agua que tengas almacenada y del caudal de salida. Calcula el volumen de tu depósito de agua con la calculadora de volumen de depósitos de la herramienta Omni Calculator. Obtén el valor en litros. Determina cuántos litros consumes al día . Divide la cantidad de agua que tienes entre tu consumo diario. El resultado es cuántos días de agua tienes.

Q: ¿Por qué preferimos los depósitos de agua cilíndricos a los cuadrados?

Hay dos razones principales por las que preferimos los depósitos cilíndricos a los rectangulares: Los depósitos cilíndricos resisten mejor las tensiones que los rectangulares. Así, los fabricantes necesitan menos material para construirlo. Los depósitos rectangulares son más difíciles de limpiar , sobre todo en las esquinas.

Q: ¿Cuál es el volumen de un barril de petróleo?

218.7 litros. Un barril de petróleo tiene un diámetro de 0.572 m y una altura de 0.851 m. Introduce estas cifras en la fórmula siguiente: Volumen = π × (d/2)² × h = 3.141 × (0.572/2)² × 0.851 = 0.2187 m² = 218.7 litros

¡Nuevo!

Índice general

Cómo utilizar la calculadora del volumen de un tanque Fórmula del volumen del depósito cilíndrico Calculadora de volumen de depósito rectangular (prisma rectangular)Fórmula para el volumen de una cápsula Volumen del depósito elíptico (depósito ovalado)Volumen de un tronco; depósito en forma de cono truncado Volumen del depósito de fondo cónico (depósito cónico) y depósitos de parte superior cónica Preguntas frecuentes

Con esta calculadora de volumen de depósitos, puedes estimar fácilmente el volumen de tu contenedor. Elige entre diez formas de depósito diferentes: desde depósitos rectangulares y cilíndricos estándar hasta depósitos en forma de cápsula y elípticos. Incluso puedes hallar el volumen de un depósito tipo tronco cónico. Sólo tienes que introducir las dimensiones de tu depósito, y esta herramienta calculará el volumen total del depósito por ti. También puedes indicar la altura de llenado, que se utilizará para hallar el volumen lleno.

¿Te preguntas cómo lo hace? Desplázate hacia abajo y encontrarás todas las fórmulas que necesitas: el volumen de un depósito cápsula, de un depósito elíptico o de los tan utilizados depósitos de fondo cónico (a veces llamados depósitos de tronco cónico), ¡así como muchas más!

¿Buscas otros tipos de depósitos con formas diferentes y para otras aplicaciones? Consulta nuestra calculadora de volumen para averiguar el volumen de los sólidos tridimensionales más comunes. Para algo más especializado, también puedes echar un vistazo a la calculadora de acuarios y a la calculadora de volumen de piscinas para encontrar soluciones a los problemas cotidianos de volumen.

Cómo utilizar la calculadora del volumen de un tanque

Esta calculadora de volumen de depósitos es una sencilla herramienta que te ayuda a encontrar el volumen del depósito, así como el volumen de la parte llena. Puedes elegir entre diez formas de depósito

Cilindro vertical;
Cilindro horizontal;
Prisma rectangular (caja);
Cápsula vertical;
Cápsula horizontal;
Óvalo vertical (elíptico);
Óvalo horizontal (elíptico);
Parte inferior del cono;
Parte superior del cono;
Tronco (por ejemplo, cónico)

"Pero, ¿cómo utilizo esta calculadora de volumen de depósitos?", te estarás preguntando. Veamos un ejemplo sencillo:

Decide la forma. Supongamos que queremos hallar el volumen de un depósito cilíndrico vertical: elige esa opción en la lista desplegable. A continuación aparecerá la imagen esquemática del depósito; ¡asegúrate de que es la que quieres!
Introduce las dimensiones del depósito. En nuestro caso, tenemos que escribir la longitud y el diámetro. En nuestro ejemplo, son iguales a $32\ \mathrm{cm}$ y $24\ \mathrm{cm}$ , respectivamente. Además, podemos introducir la altura de llenado $28\ \mathrm{cm}$ .
**El volumen total del depósito es $14.48\ \mathrm{litros}$ , y el volumen del líquido en su interior es $12.67\ \mathrm{l}$ . Como siempre, puedes cambiar las unidades haciendo clic en las propias unidades de volumen. ¡Muy fácil!

Fórmula del volumen del depósito cilíndrico

Para calcular el volumen total de un depósito cilíndrico, sólo necesitamos conocer el diámetro (o radio) del cilindro y la altura del cilindro (que puede llamarse longitud si está en posición horizontal).

Depósito cilíndrico vertical

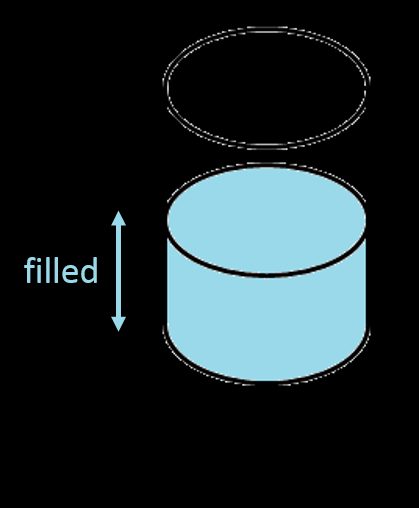
Podemos hallar el volumen total de un depósito cilíndrico con la fórmula estándar para el volumen: el área de la base multiplicada por la altura. Un círculo es la forma de la base, por lo que su área, según la conocida ecuación, es igual a $\pi \times \mathrm{radio}^2$ . Por tanto, la fórmula para el volumen de un depósito cilíndrico vertical es la siguiente:

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro\ vertical}}} &= \pi \times r^2 \times h\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times h, \end{split}

donde

$r$ - Radio de la base;
$h$ - Altura del cilindro.

Si queremos calcular el volumen lleno, tenemos que encontrar el volumen de un cilindro "más corto", ¡así de fácil!

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro\ vertical}}} &= \pi \times r^2 \times f\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times f, \end{split}

donde $f$ es la altura de la parte llena del cilindro.

Depósito cilíndrico horizontal

El volumen total de un depósito cilíndrico horizontal puede hallarse de forma análoga: es el área del extremo circular multiplicada por la longitud del cilindro:

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro\ horizontal}}} &= \pi \times r^2 \times l\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times l, \end{split}

Sección transversal de un depósito cilíndrico parcialmente lleno.

Las cosas se complican cuando queremos hallar el volumen del cilindro horizontal parcialmente lleno. En primer lugar, necesitamos hallar el área de la base: el área del segmento circular cubierto por el líquido:

A_{\mathrm{\tiny segmento}} = \frac{1}{2}\times r^2 \times (\theta-\text{sen}(\theta)),

donde $r$ es el radio de la base, y $\theta$ es el ángulo central del segmento. El ángulo $\theta$ puede hallarse a partir de la fórmula del coseno:

\cos\left(\frac{\theta}{2}\right) = \frac{r-f}{f},

donde $f$ es la altura de la sección rellena de la base.

Por tanto:

\theta= 2\times \arccos\left(\frac{r-f}{f}\right)

Y por último, la fórmula del volumen de un cilindro horizontal parcialmente lleno $V_{\scriptsize{\mathrm{cil\ parcial}}}$ es:

\small V_{\scriptsize{\mathrm{cil\ parcial}}} = 0.5\times r^2\times(\theta -\sin(\theta))\times l,

donde:

\theta = 2\times \arccos\left(\frac{r-f}{r}\right)

Si el cilindro está más de medio lleno, entonces es más fácil restar la parte del depósito vacía del volumen total.

Calculadora de volumen de depósito rectangular (prisma rectangular)

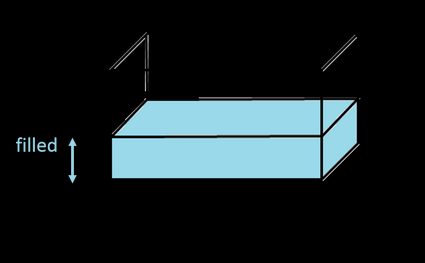
Depósito rectangular de dimensiones marcadas.

Si te preguntas cómo calcular el volumen de un depósito rectangular (también conocido como cuboide, caja o hexaedro rectangular), ¡no busques más! Puede que conozcas este depósito como depósito rectangular, pero ése no es su nombre correcto, ya que un rectángulo es una forma 2D, por lo que no tiene volumen.

Para hallar el volumen del prisma rectangular, multiplica todas las dimensiones del depósito:

V_{{\mathrm{prisma\ rectangular}}} = h\times a\times l,

donde:

$h$ - La altura del depósito;
$a$ - La anchura;
$l$ - La longitud del depósito.

Si quieres saber cuál es el volumen del líquido de un depósito, basta con cambiar la variable altura total por altura de llenado ( $f$ )en la fórmula del volumen del depósito rectangular. El volumen de un prisma rectangular lleno, $V_{\scriptsize{\mathrm{parcial}}}$ , es:

V_{{\mathrm{parcial}}} = f\times a\times l,

donde $f$ es la altura de la parte rellena.

Para esta calculadora del volumen del depósito, no importa si el depósito está en posición horizontal o vertical. Sólo asegúrate de que la altura de llenado y altura total están en el mismo eje.

Fórmula para el volumen de una cápsula

Nuestra herramienta define una cápsula como dos semiesferas separadas por un cilindro. Para calcular el volumen total de una cápsula, basta con sumar el volumen de la esfera a la parte cilíndrica:

V_{\scriptsize{\mathrm{cap}}} = \pi\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\!\times\!\left(\frac{4}{3}\!\times\!\frac{d}{2}\!+\!l\right)

Dependiendo de la posición del depósito, los cálculos del volumen de llenado diferirán un poco:

1. Para depósito de cápsula horizontal

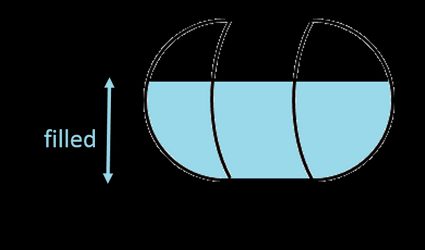
Horizontal capsule tank with marked dimensions.

Como las semiesferas de ambos extremos del depósito son idénticas, forman un casquete esférico: añade esta parte $V_{\scriptsize{\mathrm{esf\ parcial}}}$ a la parte del cilindro horizontal $V_{\scriptsize{\mathrm{cil\ parcial}}}$ (consulta el párrafo anterior) para calcular el volumen del líquido en una cápsula horizontal llena ( $V_{\scriptsize{\mathrm{cap\ parcial}}}$ ):

\begin{split} &V_{\scriptsize{\mathrm{cap\ parcial}}} = V_{\scriptsize{\mathrm{cil\ parcial}}}+V_{\scriptsize{\mathrm{esf\ parcial}}}\\[.6em] &= \frac{1}{2}\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\! \times\! (\theta-\sin(\theta))\times l \\[1em] &\quad+\frac{\pi\times f^2}{3}\!\times\!\left(\frac{3}{2}\times d-f\right), \end{split}

donde:

$d$ - Diámetro del depósito;
$f$ - Altura de llenado;
$\theta$ - Ángulo correspondiente al sector llenado de la cuba cilíndrica.

2. Para depósito de cápsula vertical

La fórmula difiere para distintas alturas de llenado. En todas las fórmulas siguientes, nos encontraremos con estas cantidades

$d$ - Diámetro del depósito;
$f$ - Altura alcanzada por el líquido;
$l$ - Longitud de la sección cilíndrica.

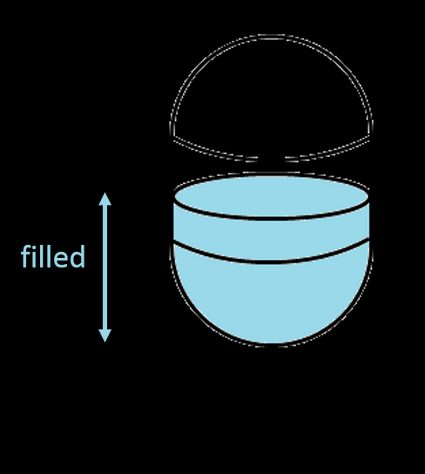
Depósito cápsula vertical de dimensiones marcadas.

Si $f < d/2$ , entonces el líquido sólo está en la parte inferior de la semiesfera, por lo que sólo necesitamos la fórmula del volumen de un casquete esférico:

\\[2em] V_{\scriptsize{\mathrm{cap\ parcial\ vertical}}} = \frac{(\pi\!\times \!f)^2}{3}\!\times\!\left(\frac{3}{2}\!\times \!d - f\right) \\[2em]

Si $d/2 < f < d/2 +l$ , entonces tenemos que añadir el volumen de la semiesfera y el cilindro "más corto":

\quad\ \ \ \begin{split} &V_{\scriptsize{\mathrm{cap\ parcial\ vertical}}} = \frac{2}{3}\times \pi\left(\frac{d}{2}\right)^3\\[1em] &\qquad+\pi\times\left(\frac{d}{2}\right)^2\times\frac{f-d}{2} \end{split}

Si $d/2 + l < f$ , significa que tenemos la semiesfera inferior y el cilindro llenos, por lo que sólo tenemos que restar el casquete esférico (parte vacía) de todo el volumen:

\begin{split} &V_{\scriptsize{\mathrm{cap\ parcial\ vertical}}} = V_{\scriptsize{\mathrm{cap}}}\! -\! \frac{\pi\times(l+d-f)^2}{3}\\ &\qquad\ \ \times\left(\frac{3}{2}\times d - (l+d-f)\right) \end{split}

Volumen del depósito elíptico (depósito ovalado)

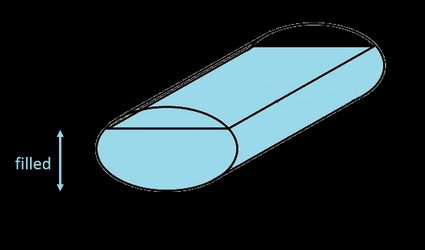
Depósito oval horizontal con dimensiones marcadas.

En nuestra calculadora, definimos un depósito ovalado como un depósito cilíndrico con un extremo elíptico (no en forma de estadio, como se define a veces). Para hallar el volumen total de un depósito elíptico, debes multiplicar el área de la elipse por la longitud del depósito:

V_{\scriptsize{\mathrm{elipse}}} = \pi\!\times\!w\!\times\!l\!\times\!\frac{h}{4},

donde:

$wa$ - La anchura del depósito;
$h$ - La altura del depósito;
$l$ - La longitud del depósito.

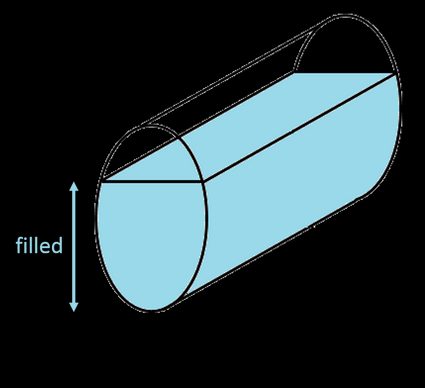
Depósito oval vertical de dimensiones marcadas.

Por fin, ¡otra fórmula fácil! Por desgracia, hallar el volumen de un depósito parcialmente lleno, tanto en posición horizontal como vertical, no es tan sencillo. Tienes que utilizar la fórmula del área del segmento de la elipse y multiplicar el resultado por la longitud del depósito:

\begin{split} &V_{\scriptsize{\mathrm{eli\ parcial}}} = l\!\times\!h\!\times\!\frac{a}{4}\\[1em] &\qquad\times\!\left[\arccos\left(1\!-\!\frac{2\!\times\!f}{h}\right)\right.\\[1.5em] &\!\!\left.-\!\left(\!1\!-\!\frac{2\!\times\!f}{h}\!\right)\!\times\!\sqrt{\frac{4\!\times\!f}{h}\!-\!\frac{4\!\times\!f^2}{h^2}}\right] \end{split}

Volumen de un tronco; depósito en forma de cono truncado

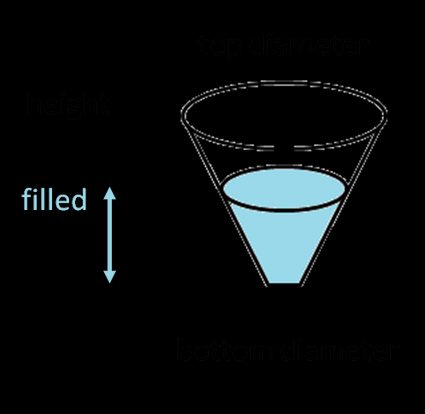
Depósito en tronco con dimensiones marcadas.

Para calcular el volumen del cono truncado (una forma particular que conocimos en nuestra calculadora de conos truncados 🇺🇸), utiliza la fórmula:

\begin{split} &V_{\scriptsize{\mathrm{tronco}}} = \frac{1}{3}\times\pi\times h_{\mathrm{cono}}\\[1em] &\qquad\times\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\!+\! \frac{d_{\mathrm{sup}}}{2}\!\times\!\frac{d_{\mathrm{inf}}}{2}\!\right.\\[1em] &\qquad\qquad \left.+\!\left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right), \end{split}

donde:

$d_{\mathrm{sup}}$ - Diámetro superior del tronco;
$d_{\mathrm{inf}}$ - Diámetro inferior del tronco;
$h_{\mathrm{cono}}$ - Altura del depósito.

Depósito en tronco con dimensiones y nivel de líquido marcados.

Si quieres hallar el volumen del tronco parcialmente rellenado para una altura de relleno dada, calcula primero el radio superior de la parte rellenada:

R = \frac{1}{2} \times d_{\mathrm{sup}}\times \frac{f+z}{h_{\mathrm{cono}}+z},

donde:

z = h_\mathrm{cono} \times \frac{d_{\mathrm{inf}}}{d_{\mathrm{sup}}-d_{\mathrm{inf}}}

(Puedes deducir la fórmula a partir de la semejanza de los triángulos)

Después, sólo tienes que hallar el nuevo volumen del tronco:

\begin{split} &V_{\scriptsize{\mathrm{tronco\ parcial}}}=\frac{1}{3} \times \pi \times f \\ &\ \ \times \!\left(R^2 \!+ \!R\! \times \!\frac{d_{\mathrm{inf}}}{2} + \left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right) \end{split}

Volumen del depósito de fondo cónico (depósito cónico) y depósitos de parte superior cónica

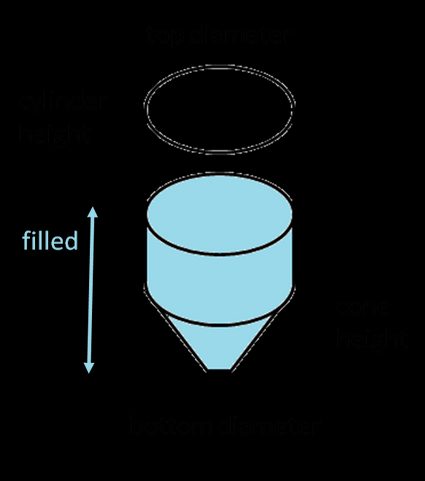
Depósito de fondo cónico con dimensiones marcadas.

Hallar el volumen total de un depósito de fondo cónico no es tan difícil: basta con sumar el volumen de la parte del tronco al volumen de la parte cilíndrica:

\begin{split} &V_{\scriptsize{\mathrm{f\ cono}}} = V_{\scriptsize{\mathrm{tronco}}} + V_{\scriptsize{\mathrm{cil}}}\\[1em] & =\frac{1}{3}\times\pi\times h_{\mathrm{cono}} \times\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\right.\\[1.4em] &\qquad \left.+ \frac{d_{\mathrm{sup}}}{2}\!\times\!\frac{d_{\mathrm{inf}}}{2}\!+\!\left(\frac{d_{\mathrm{in}}}{2}\right)^2\right)\\[1.4em] &\qquad+\pi\times\left(\frac{d_{\mathrm{sup}}}{2}\right)^2\times h_{\mathrm{cil}}, \end{split}

donde:

$d_{\mathrm{top}}$ - Diámetro superior del tronco;
$d_{\mathrm{bot}}$ - Diámetro inferior del tronco;
$h_{\mathrm{cono}}$ y $h_{\mathrm{cil}}$ - Las alturas de los dos sub-depósitos.

Para calcular el depósito parcialmente lleno, basta con sumar la parte del tronco y la parte cilíndrica, según el nivel del líquido lleno, utilizando las ecuaciones anteriores.

El cálculo del volumen total del depósito superior cónico es exactamente el mismo que el del depósito inferior cónico. La única diferencia es cuando quieres hallar la parte llena: obviamente, primero se llena la parte cilíndrica, y sólo después la parte del tronco.

🙋 ¿Has calculado todos tus volúmenes utilizando unidades métricas, pero necesitas unidades imperiales? No te preocupes, porque Omni tiene una práctica solución para todas tus necesidades: ¡utiliza nuestra herramienta conversión de volúmenes 🇺🇸 para convertir rápidamente entre unidades de volumen!

Preguntas frecuentes

¿Cómo calcular el volumen de un depósito de agua?

Puedes probar con la calculadora de volumen de depósitos de la herramienta Omni Calculator o hacer lo siguiente:

Obtén el radio interior y la altura del depósito.
Eleva al cuadrado el radio y luego multiplica por pi (3.14159...). Enhorabuena, ya tienes el área del depósito de agua.
Multiplica el resultado por la altura, y obtendrás el volumen del depósito.

¿Cómo calcular la cilindrada de mi motor?

Los expertos en automóviles lo llaman cilindrada del motor, y puedes calcularla del siguiente modo:

Obtén el volumen de uno de los cilindros de tu motor. Puedes probar con la calculadora de volumen del depósito de la herramienta Omni Calculator u obtener el radio y la altura del cilindro (carrera del pistón del motor).
Eleva al cuadrado el radio, multiplica por pi (3.14159...), y luego por la carrera del pistón.
Multiplica el volumen de un cilindro por el número de cilindros de tu motor, y obtendrás la cilindrada.

¿Cuánto tiempo puede durar el agua almacenada en un depósito?

Dependerá de la cantidad de agua que tengas almacenada y del caudal de salida.

Calcula el volumen de tu depósito de agua con la calculadora de volumen de depósitos de la herramienta Omni Calculator. Obtén el valor en litros.
Determina cuántos litros consumes al día.
Divide la cantidad de agua que tienes entre tu consumo diario. El resultado es cuántos días de agua tienes.

¿Por qué preferimos los depósitos de agua cilíndricos a los cuadrados?

Hay dos razones principales por las que preferimos los depósitos cilíndricos a los rectangulares:

Los depósitos cilíndricos resisten mejor las tensiones que los rectangulares. Así, los fabricantes necesitan menos material para construirlo.
Los depósitos rectangulares son más difíciles de limpiar, sobre todo en las esquinas.

¿Cuál es el volumen de un barril de petróleo?

218.7 litros. Un barril de petróleo tiene un diámetro de 0.572 m y una altura de 0.851 m. Introduce estas cifras en la fórmula siguiente:

Volumen = π × (d/2)² × h = 3.141 × (0.572/2)² × 0.851 = 0.2187 m² = 218.7 litros

Calculadora del volumen de un tanque

Álvaro Díez

Cómo utilizar la calculadora del volumen de un tanque

Fórmula del volumen del depósito cilíndrico

Calculadora de volumen de depósito rectangular (prisma rectangular)

Fórmula para el volumen de una cápsula

Volumen del depósito elíptico (depósito ovalado)

Volumen de un tronco; depósito en forma de cono truncado

Volumen del depósito de fondo cónico (depósito cónico) y depósitos de parte superior cónica

¿Cómo calcular el volumen de un depósito de agua?

¿Cómo calcular la cilindrada de mi motor?

¿Cuánto tiempo puede durar el agua almacenada en un depósito?

¿Por qué preferimos los depósitos de agua cilíndricos a los cuadrados?

¿Cuál es el volumen de un barril de petróleo?

Dimensiones

Volumen