Calculadora de la desviación estándar de la media muestral

Calcular la desviación estándar de la media muestral (también conocida como desviación estándar de la distribución muestral de la media) es una forma excelente de comprender cómo influye el tamaño de muestra en el error de nuestras estimaciones.

Cuando la desviación estándar de la media se multiplica por un valor crítico, como la puntuación z o el estadístico t, obtenemos un margen de error que permite establecer un intervalo de confianza de nuestra predicción. Por tanto, calcular la desviación estándar de la distribución muestral de la media indica dónde podría estar la media poblacional.

En primer lugar, es importante aclarar que este término se conoce con diversos nombres como:

• La desviación estándar de la media;
• La desviación estándar de la media muestral;
• La desviación estándar de la distribución de las medias muestrales;
• La desviación estándar de la distribución muestral de la media muestral.

También es esencial conocer algunas definiciones y conceptos:

• Estadístico: una estimación puntual o característica numérica de una muestra (es decir, la media de la muestra). Es diferente de un parámetro, como la media poblacional.
• Distribución muestral: la distribución de probabilidad de un estadístico muestreado aleatoriamente. En otras palabras, es la distribución de todos los valores posibles que podría tomar un estadístico utilizando el mismo tamaño de muestra.
• Distribución muestral de la media: es una ampliación del concepto anterior. Si tienes una población, tomas infinitas muestras, cada una de tamaño n, y representas sus medias en un histograma, obtienes una distribución de probabilidad. Esa distribución de probabilidad es lo que llamamos distribución muestral de la media, y como cualquier otra distribución, tiene su propia media y desviación estándar.

El siguiente diagrama muestra cómo generar una distribución muestral de la media. En realidad, no utilizamos solo seis muestras, sino un número casi infinito (es decir, 100 000).

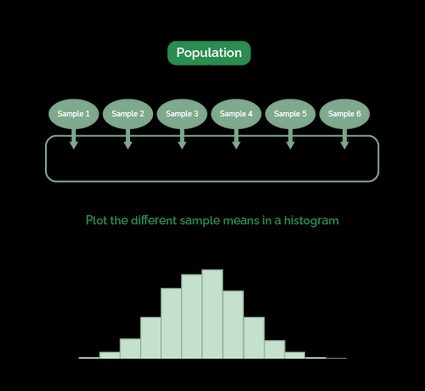
Dicho esto, podemos definir la desviación estándar media como la desviación estándar de una distribución de medias (como la que se muestra en el último diagrama). Además, la media de esta distribución muestral es igual a la media poblacional.

Ahora que ya conoces el concepto, veamos cómo calcular la desviación estándar de la media muestral.

La diferencia entre la distribución de una muestra una distribución muestral es:

• Distribución muestral: es el término que solemos oír. Se refiere a la distribución de probabilidad de un estadístico muestreado aleatoriamente. La distribución muestral de la media es un ejemplo.
• Distribución de una muestra: da cuenta de la distribución de las observaciones dentro de una sola muestra. Cada distribución de una muestra posee una media, que ayuda a formar la distribución muestral.

La fórmula para hallar la desviación estándar de la media muestral es:

σ_X̄ = σ/√n

donde:

• σ_X̄ - Desviación estándar de la media muestral;
• σ - Desviación estándar poblacional;
• n - Tamaño de muestra.

Anteriormente, dijimos que si conocemos la media de la distribución muestral (μ_X̄), también conocemos la media poblacional (μ), ya que son iguales (μ_X̄ = μ). En la práctica, nunca conocemos μ_X̄, pero podemos estimarla utilizando la media muestral (X̄).

σ_X̄ indica cómo se aproxima X̄ a μ. Cuanto menor sea σ_X̄, más se acercará μ a nuestra estimación. Como σ es constante, aumentar el tamaño de muestra es la única forma de disminuir σ_X̄. Por lo tanto, aumentar n es una forma de reducir el error de muestreo 🇺🇸 de nuestras estimaciones.

Sabemos que la media y la desviación estándar de la estatura de la población femenina estadounidense adulta son aproximadamente μ = 161.3 cm y σ = 7.1 cm. Ahora, supongamos que tomas muestras aleatorias de 100 mujeres y les tomas la altura media cada vez. ¿Cuál es la desviación estándar de la media muestral?

Para conocer la respuesta, sigue estos pasos:

1. Introduce 7.1 en la casilla de desviación estándar poblacional.
2. Introduce 100 en la casilla de tamaño de muestra.
3. Y ya está. La respuesta debe ser 0.71. Por tanto, la desviación estándar de las distribuciones muestrales de medias n = 100 es 0.71.

Puedes comprobar los resultados utilizando la fórmula: $σ_{\bar X} = \frac{σ}{\sqrt{n}} = \frac{7.1}{\sqrt{100}} = 0.71$