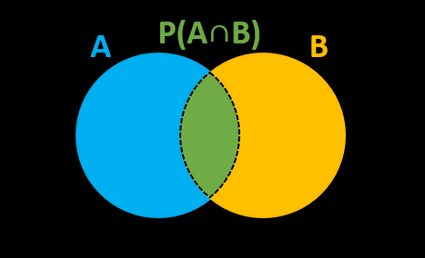
Calculadora de probabilidad

Con la calculadora de probabilidad, puedes averiguar las relaciones de probabilidad entre dos sucesos distintos. Por ejemplo, si la probabilidad de que ocurra A es del 50%, y lo mismo para B, ¿cuál es la probabilidad de que ocurran ambos, de que ocurra solo uno, de que ocurra al menos uno, o de que no ocurra ninguno?

Nuestra calculadora de probabilidades te brinda seis escenarios, más otros seis si introduces cuántas veces está “echada la suerte”, por así decirlo. Siempre que sepas cómo hallar la probabilidad de sucesos individuales, te ahorrará mucho tiempo.

Leyendo a continuación, podrás:

• Descubrir cómo utilizar correctamente la calculadora de probabilidades.
• Comprobar cómo hallar la probabilidad de sucesos individuales.
• Leer múltiples ejemplos sobre el uso de la probabilidad, incluidas las fórmulas de probabilidad condicional.
• Estudiar la diferencia entre probabilidad teórica y empírica.
• Incrementar tus conocimientos sobre la relación entre probabilidad y estadística.

¿Has venido aquí específicamente para conocer tus probabilidades de ganar una apuesta o de ganar la lotería? ¡Nuestra calculadora de probabilidades de ganar y la calculadora de lotería 🇺🇸 te ayudarán!

La definición básica de probabilidad es la proporción entre todos los resultados favorables y el número de todos los resultados posibles.

Los valores permitidos de una probabilidad única varían de 0 a 1, por lo que también se suele escribir las probabilidades como porcentajes. La probabilidad de un único evento puede expresarse así:

• La probabilidad de A: P(A),
• La probabilidad de B: P(B),
• La probabilidad de +: P(+),
• La probabilidad de ♥: P(♥), etc.

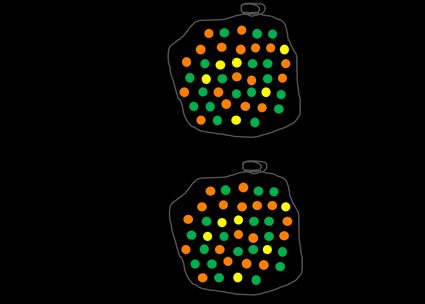
Veamos un ejemplo con bolas de distintos colores. Tenemos una bolsa llena de bolas naranjas, verdes y amarillas. Nuestro suceso A es sacar una bola al azar de la bolsa. Podemos definir Ω como el conjunto completo de bolas. La probabilidad del suceso Ω, que significa elegir cualquier bola, es, naturalmente, 1. De hecho, la suma de todos los sucesos posibles en un conjunto dado es siempre igual a 1.

Veamos ahora algo más desafiante: ¿cuál es la probabilidad de tomar una bola naranja? Para responder a esta pregunta, tienes que hallar el número de todas las bolas naranjas y dividirlo por el número total de bolas en la bolsa. Puedes hacerlo para cualquier color, como el amarillo, y te darás cuenta de que cuantas más bolas haya de un color determinado, mayor será la probabilidad de elegirla de la bolsa si el proceso es totalmente aleatorio.

Consulta nuestra calculadora de probabilidad de 3 sucesos 🇺🇸 y calculadora de probabilidad condicional 🇺🇸 para determinar las probabilidades de sucesos múltiples.

Podemos definir un evento o suceso complementario (escrito como Ā o A'), que significa no A. En nuestro ejemplo, la probabilidad de sacar una bola que NO sea naranja se evalúa como el número de todas las bolas de color distinto al naranja dividido por el total de bolas. La suma P(A) + P(Ā) es siempre 1, porque no hay ninguna otra opción (como mitad de una bola o una bola seminaranja).

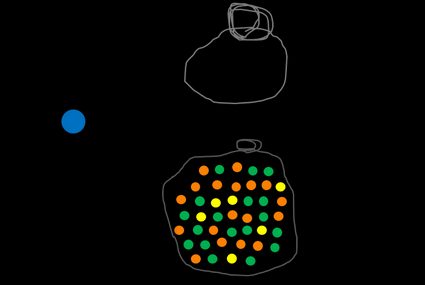
Ahora, intenta hallar la probabilidad de obtener una bola azul. No lo conseguirás, por mucho que lo intentes, ya que no hay ni una en la bolsa, por lo que el resultado es igual a 0.

Utilizamos la probabilidad intuitivamente todo el tiempo. Saber cuantificar la probabilidad es esencial para el análisis estadístico. Además, dado un conjunto de datos discretos, la frecuencia relativa de cada valor es sinónimo de la probabilidad de su ocurrencia.

¿Buscas algo ligeramente diferente? Echa un vistazo a nuestra calculadora de probabilidad postprueba 🇺🇸. 🎲

Para aprovechar al máximo nuestra calculadora, tendrás que seguir los siguientes pasos:

1. Define el problema que quieres resolver.

Tu problema debe consolidarse en dos eventos independientes.

2. Halla la probabilidad de cada suceso.

Ahora, cuando sepas cómo estimar la probabilidad de un único suceso, solo tendrás que calcularla para todos los casos.

3. Escribe el porcentaje de probabilidad de cada suceso en los campos correspondientes.

Una vez introducidos, la calculadora de probabilidades se rellenará inmediatamente con la probabilidad exacta para 6 escenarios diferentes:

• que ocurran ambos sucesos,
• que ocurra al menos uno de los sucesos,
• que ocurra exactamente uno de los eventos,
• que no ocurra ninguno de los dos sucesos,
• que no ocurra únicamente el primer evento, y
• que no ocurra únicamente el segundo evento.

También puedes escoger ver todas las seis opciones de arriba. Adicionalmente, nuestra calculadora también mostrará la probabilidad de seis escenarios más, dado un número determinado de ensayos:

• que A siempre ocurra,
• que A no ocurra nunca,
• que A ocurra al menos una vez
• que B siempre ocurra,
• que B nunca ocurra, y
• que B ocurra al menos una vez.

Puedes cambiar el número de ensayos y cualquier otro campo de la calculadora, y los demás campos se ajustarán automáticamente. Esta función te ahorrará mucho tiempo si quieres averiguar, por ejemplo, cuál debería ser la probabilidad del suceso B para que la probabilidad de que ocurran ambos sea del 50%.

Si el conjunto de eventos posibles es extremadamente grande y solo unos pocos resultados son favorables, la probabilidad resultante es minúscula, por ejemplo, P(A) = 0.0001. Es conveniente utilizar la notación científica para no confundir el número de ceros.

Una de las consideraciones más cruciales en el mundo de las probabilidades es acerca de si los sucesos son independientes o no. Dos sucesos son independientes si la ocurrencia del primero no afecta a la probabilidad de que ocurra el segundo. Por ejemplo, si lanzamos un dado de seis caras perfectamente equilibrado, la posibilidad de obtener un dos ⚁ es igual a 1/6 (al igual que la probabilidad de obtener un cuatro ⚃ o cualquier otro número).

Supongamos que tiras un dado dos veces, y obtienes un cinco ⚄ en la primera. Si te preguntas cuál es la probabilidad de obtener un dos ⚁ en la segunda tirada, la respuesta es 1/6, una vez más debido a la independencia de los sucesos.

La forma de pensar, y los cálculos, cambian si uno de los evento afecta a todo el sistema. En este caso, hablamos de probabilidad condicional.

Supongamos que tenemos 10 bolas de billar con números diferentes, del ➀ al ➉. Eliges una bola al azar, por lo que la probabilidad de obtener la ➆ es, precisamente, 1/10. Ahora supón que eliges el tres ➂ y lo borras del juego. Entonces te preguntas, una vez más, cuál es la probabilidad de obtener el siete ➆. La situación ha cambiado, porque la probabilidad de tomar un número particular de 9 bolas posibles es 1/9. En otras palabras, podemos plantear la pregunta “¿Cuál es la probabilidad de elegir ➆, SI la primera bola era ➂?”

Veamos otro ejemplo: imagina que vas a presentarte a un examen de estadística. Sabes por tus compañeros mayores que es difícil, y que la probabilidad de que apruebes en el primer trimestre es de 0.5 (18 de 36 alumnos aprobaron el año pasado). Entonces hagámonos una pregunta: “¿Cuál es la probabilidad de aprobar SI ya has estudiado el tema?” 20 personas admitieron haber repasado sus apuntes al menos una vez antes del examen, y 16 de ellas lo consiguieron, lo que significa que la respuesta a la última pregunta es 0.8. Este resultado indica que esta condición adicional importa significativamente si queremos averiguar si estudiar cambia algo o no.

Si todavía no comprendes del todo el concepto de probabilidad condicional, probemos con otro ejemplo: tienes que conducir desde la ciudad X hasta la ciudad Y en automóvil. La distancia entre ambas es de unos 150 km. Con un tanque lleno, puedes recorrer hasta 400 kilómetros. Si no conoces el nivel de combustible del automóvil, puedes estimar la probabilidad de llegar con éxito al destino sin recargar. ¿Y que si alguien ya ha llenado el depósito? Ahora estás casi seguro de que podrás llegar, a menos que otros problemas te lo impidan.

La expresión formal para la probabilidad condicional, denotada como P(A|B), P(A/B) o P_B(A), puede calcularse como:

P(A|B) = P(A∩B) / P(B),

donde P(B) es la probabilidad de un suceso B, y P(A∩B) es la intersección de ambos sucesos. Por otra parte, podemos estimar la intersección de dos sucesos sabiendo una de las probabilidades condicionales:

• P(A∩B) = P(A|B) × P(B) o
• P(A∩B) = P(B|A) × P(A).

Resulta más fácil entender el concepto de fórmula de probabilidad condicional con diagramas de árbol. Preguntamos a alumnos de una clase si les gustan las Matemáticas y la Física. Un suceso M denota el porcentaje de alumnos que les gustan las Matemáticas, y F para Física:

Existe un famoso teorema que relaciona las probabilidades condicionales de dos sucesos. Se llama teorema de Bayes, y la fórmula es la siguiente:

P(A|B) = P(B|A) × P(A) / P(B)

Puedes preguntar: “¿Cuál es la probabilidad de A dado B si conozco la probabilidad de B dado A?”. Este teorema proporciona a veces resultados sorprendentes y poco intuitivos. Los ejemplos más comúnmente utilizados son análisis de medicamentos y detección de enfermedades, que tiene mucho en común con el riesgo relativo de enfermedad en una población. Trabajemos con el segundo. En un grupo de 1000 personas, 10 de ellas padecen una rara enfermedad. A todos se les hizo una prueba, que da un resultado correcto en el 95% de los casos. Así que ahora queremos hallar la probabilidad de que una persona esté enferma si el resultado de su prueba es positivo.

Sin hacer cuentas, puedes predecir, por intuición, que el resultado debe estar en torno al 90%, ¿verdad? Hagamos algunos cálculos y estimemos la respuesta correcta.

1. Emplearemos la siguiente notación: S = sano, E = enfermo, + = prueba positiva, - = prueba negativa.
2. Reescribe la información del texto anterior en forma de probabilidades: P(S) = 0.99, P(E) = 0.01, P(+|E) = 0.95, P(-|E) = 0.05, P(+|S) = 0.05, P(-|E) = 0.95.
3. Calcula la probabilidad total de que una prueba sea positiva: P(+) = P(+|E) × P(E) + P(+|S) × P(S) = 0.95 × 0.01 + 0.05 × 0.99 = 0.059.
4. Utiliza el teorema de Bayes para hallar la probabilidad condicional P(E|+) = P(+|E) × P(E) / P(+) = 0.95 × 0.01 / 0.059 = 0.161.

Mmm… no es tan alto, ¿verdad? Resulta que este tipo de paradoja aparece cuando existe una desproporción importante entre el número de personas sanas y el número de personas enfermas, o en general, entre dos grupos distintos. Si el resultado es positivo, vale la pena repetir la prueba para hacer un diagnóstico adecuado.

Podemos distinguir dos tipos de distribuciones de probabilidad, dependiendo de si las variables aleatorias son discretas o continuas.

• Una distribución de probabilidad discreta describe la probabilidad de ocurrencia para eventos contables y distintos. Uno de los ejemplos es la probabilidad binomial, que tiene en cuenta la probabilidad de algún tipo de éxito en varios ensayos, por ejemplo, al lanzar una moneda. En cambio, en la distribución de Pascal (también conocida como binomial negativa) se da el número fijo de aciertos, y se busca estimar el número total de ensayos.

  La distribución de Poisson es otra distribución de probabilidad discreta y, en realidad, es un caso particular de la binomial, que puedes calcular con nuestra calculadora de la distribución de Poisson 🇺🇸. Una función de probabilidad (o función de masa de probabilidad) puede interpretarse como otra definición de distribución de probabilidad discreta: asigna un valor determinado a cada número. La distribución geométrica es un ejemplo excelente de utilización de la función de masa de probabilidad. Lee más sobre esto en nuestra calculadora de distribución geométrica 🇺🇸.

• Una distribución de probabilidad continua contiene información sobre eventos incontables. Es imposible predecir la probabilidad de un único suceso (como en una distribución discreta), en cambio, podemos encontrar el suceso dentro de un rango de variables. La distribución normal es una de las distribuciones continuas más conocidas. Describe un montón de propiedades dentro de una población, por ejemplo, la altura de las personas adultas o el cociente intelectual. La función que describe la probabilidad de ver un resultado a partir de un rango determinado de valores se denomina función de densidad de probabilidad.

Si estás más avanzado en teoría de la probabilidad y cálculos, seguro has trabajado con la distribución SMp(x) 🇺🇸 que tiene en cuenta la combinación de varias funciones de probabilidad (tanto discretas como continuas).

Para cada distribución de probabilidad, podemos construir la función de distribución acumulativa (FDA). Esta función te dice cuál es la probabilidad de que alguna variable tome un valor menor o igual a un número dado.

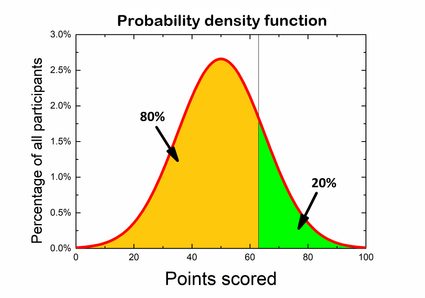
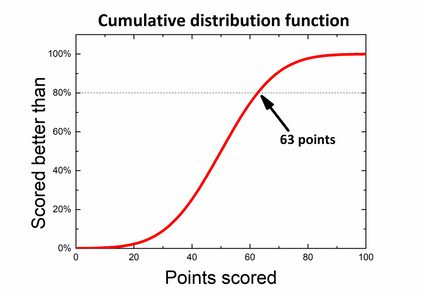
Supongamos que participas en un concurso de conocimientos generales. El concurso consta de 100 preguntas, y ganas 1 punto por una respuesta correcta. Si tu respuesta es incorrecta, no sumas puntos. Muchas personas ya han terminado, y podemos obtener una distribución de probabilidad a partir de los resultados. Las reglas establecen que solo el 20% de los participantes con mejor desempeño reciben premios, así que te preguntas qué puntuación deberías obtener para ser uno de los ganadores. Si te fijas en el gráfico, puedes dividirlo de modo que el 80% del área de abajo quede a la izquierda y el 20% de los resultados queden a la derecha de la puntuación deseada. Lo que en realidad buscas es un valor p de cola izquierda.

Sin embargo, también hay otra forma de hallarlo si utilizamos una función de distribución acumulativa: ¡solo tienes que hallar el valor 80% en el eje de abscisas y el número de puntos correspondiente sin calcular nada!

Casi todos los ejemplos descritos anteriormente tienen en cuenta la probabilidad teórica. Así que podemos preguntarnos: ¿cuál es la diferencia entre probabilidad teórica y experimental (también llamada empírica)? La definición formal de probabilidad teórica es el cociente entre el número de resultados favorables y el número de todos los resultados posibles. Se basa en los datos recolectados y en el razonamiento lógico, y nos dice lo que deberíamos esperar de un experimento.

Vuelve a mirar las bolsas con bolas de colores. Hay 42 bolas en total, y 18 de ellas son naranjas. El juego consiste en coger una bola al azar de la bolsa y volverla a meter, de modo que siempre haya 42 bolas dentro. Aplicando la definición de probabilidad teórica, podemos estimar rápidamente que es 18/42, o simplificando la fracción, 3/7. Esto significa que si sacamos 14 bolas, debería haber 6 naranjas.

Por otro lado, la probabilidad experimental nos dice con precisión lo que ocurrió cuando realizamos un experimento en lugar de lo que debería ocurrir. Se basa en la razón entre el número de sucesos favorables y el número total de ensayos. Sigamos con el mismo ejemplo: tomas una bola al azar de la bolsa y repites el procedimiento 13 veces más. Supongamos que obtienes 8 bolas naranjas en 14 ensayos. Este resultado implica que la probabilidad empírica es 8/14 o 4/7.

Como puedes ver, este resultado difiere del teórico. No es de extrañar, porque cuando intentas repetir este juego una y otra vez, a veces, sacarás más, y a veces sacarás menos, y a veces sacarás justo el número predicho teóricamente. Si sumas todos los resultados, deberías notar que la probabilidad global se acerca cada vez más a la probabilidad teórica. De no ser así, podemos sospechar que elegir una bola de la bolsa no es totalmente aleatorio y que, por ejemplo, si las bolas de distintos colores tuvieran tamaños diferentes, podrías distinguirlas sin tener que mirar.

Tanto la estadística como la probabilidad son ramas de las matemáticas y se ocupan de la relación de la ocurrencia de sucesos. Sin embargo, todos deberían conocer las diferencias que las convierten en dos áreas distintas.

• La probabilidad suele ser un campo teórico de las matemáticas, e investiga las consecuencias de las definiciones y teoremas matemáticos. En cambio, la estadística en general es una aplicación práctica de las matemáticas en situaciones cotidianas e intenta atribuir sentido a las observaciones del mundo real.

• La probabilidad prevé la posibilidad de que ocurran eventos, mientras que la estadística consiste básicamente en analizar la frecuencia de ocurrencia de sucesos pasados y proporciona un modelo basado en información previa.

• Imagina a un probabilista jugando a un juego de cartas, que consiste en elegir una carta al azar de todo un mazo, sabiendo que solo ganan las picas con una proporción de probabilidades predefinida. Suponiendo que la baraja está completa y que la elección es totalmente aleatoria y equitativa, deduce que la probabilidad es igual a ¼ y puede hacer una apuesta.

• Un estadístico, primero observará el juego durante un rato para comprobar si, de hecho, el juego es equitativo. Tras verificar (con una aproximación aceptable) que el juego merece la pena, entonces preguntará al probabilista qué debe hacer para ganar más.

Seguramente hayas visto encuestas sobre candidatos electorales, y te habrás preguntado cómo pueden ser tan precisas al comparar con los resultados finales, siendo que el número de personas encuestadas es muy inferior al de la población total: aquí es cuando importa el muestreo probabilístico.

La suposición subyacente, la idea básica del muestreo, es que los voluntarios se eligen al azar con una probabilidad previamente definida. Podemos distinguir varios tipos de métodos de muestreo:

• muestreo aleatorio simple
• muestreo aleatorio por conglomerados
• muestreo sistemático
• muestreo probabilístico proporcional al tamaño
• muestreo aleatorio estratificado
• muestreo minimax
• muestreo accidental
• muestreo por cuotas
• muestreo voluntario
• muestreo panel
• muestreo de bola de nieve
• muestreo por transecto lineal
• muestreo teórico

Cada uno de estos métodos tiene sus pros y contras, pero la mayoría son beneficiosos. Las ventajas significativas del muestreo probabilístico son el ahorro de tiempo y la rentabilidad, ya que hay que encuestar a un número limitado de personas. La sencillez de este procedimiento no requiere conocimientos avanzados y puede realizarse sin mucha preparación.

Como ya te habrás dado cuenta, hay muchas áreas en las que es aplicable la teoría de la probabilidad. La mayoría son juegos con una alta influencia del azar, como tirar los dados o elegir una bola de un color específico entre 10 colores diferentes, o juegos de cartas. La lotería y los juegos de azar son los tipos de juegos que utilizan ampliamente el concepto de probabilidad y su falta de entendimiento por parte de quienes participan en los mismos. Claro, alguien gana de vez en cuando, pero la probabilidad de que esa persona seas tú es extremadamente pequeña.

La teoría de la probabilidad también se utiliza en muchos tipos diferentes de problemas. Especialmente cuando hablamos de inversiones, también conviene tener en cuenta el riesgo para elegir la opción más adecuada.

Nuestra calculadora para una blanca Navidad 🇺🇸 recoge datos históricos y emplea conocimientos de probabilidad para predecir la aparición de nieve en distintas ciudades durante la Navidad.