Calculadora de prueba t de Student

¡Te damos la bienvenida a nuestra calculadora de pruebas t!
Aquí no solo podrás realizar fácilmente pruebas t de muestra única, sino también pruebas t de dos muestras dependientes o independientes.
¿Quieres hallar el valor p de la prueba t, o quizás hallar los valores críticos de la prueba t? ¡Pues esta calculadora de pruebas t puede hacer ambas cosas! 😊

¿Qué te dice una prueba t? Echa un vistazo al texto debajo, donde explicamos qué se comprueba realmente cuando se efectúan los distintos tipos de pruebas t. También explicamos cuándo utilizar las pruebas t (en particular, si deberíamos utilizar la prueba z frente a la prueba t), y qué suposiciones deben cumplirse en los datos para que los resultados de una prueba t sean válidos. Si alguna vez has querido saber cómo hacer una prueba t a mano, te proporcionamos la fórmula necesaria para la prueba t, además de indicarte cómo determinar el número de grados de libertad en una prueba t.

Una prueba t es una de las pruebas estadísticas más populares y se ocupa del valor o valores medios de la población o poblaciones.
Hay distintos tipos de pruebas t que puedes realizar:

• una prueba t para una muestra;
• una prueba t para dos muestras; y
• una prueba t pareada.

En el siguiente apartado explicamos cuándo utilizar cuál.
Recuerda que una prueba t solo puede emplearse para uno o dos grupos. Si necesitas comparar tres (o más) medias, usa el método de análisis de la varianza (ANOVA).

La prueba t es una prueba paramétrica, lo que significa que tus datos tienen que cumplir algunas suposiciones:

• los datos son independientes; y
• los datos, al menos aproximadamente, siguen una distribución normal 🇺🇸.

Si tu muestra no se ajusta a estas suposiciones, puedes recurrir a alternativas no paramétricas. Visita nuestra calculadora de prueba U de Mann-Whitney 🇺🇸 o la calculadora de prueba de suma de rangos de Wilcoxon 🇺🇸 para obtener más información. Otras posibilidades son la prueba de los rangos con signos de Wilcoxon o la prueba de signos.

La elección de la prueba t depende de si estudias un grupo o dos grupos:

• Prueba t para una muestra única

  Elige la prueba t para una muestra para ver si la media de una población es igual a algún valor hipotético preestablecido.

  Ejemplos:

  • El volumen medio de una bebida que se vende en latas de 0.33 l: ¿es realmente igual a 330 ml?

  • El peso medio de las personas de una ciudad concreta: ¿es diferente de la media nacional?

• Prueba t para dos muestras

  Elige la prueba t para dos muestras para comprobar si la diferencia entre las medias de dos poblaciones es igual a algún valor predeterminado, cuando las dos muestras se han elegido independientemente la una de la otra.

  En concreto, puedes utilizar esta prueba para verificar si los dos grupos son diferentes entre sí.

  Ejemplos:

  • La diferencia promedio en el aumento de peso de dos grupos de personas: un grupo seguía una dieta rica en carbohidratos y el otro una dieta rica en grasas.
  • La diferencia promedio en los resultados de un examen de matemáticas de alumnos de dos universidades distintas.

  Esta prueba se denomina a veces prueba t de muestras independientes, o prueba t de muestras no pareadas.

• Prueba t pareada

  Una prueba t pareada se emplea para investigar el cambio en la media de una población antes y después de alguna intervención experimental, basándose en una muestra dependiente, es decir, cuando cada sujeto ha sido medido dos veces: antes y después del tratamiento.

  En concreto, puedes usar esta prueba para comprobar si, en promedio, el tratamiento ha tenido algún efecto sobre la población.

  Ejemplos:

  • El cambio en el rendimiento de un alumno en un examen antes y después de hacer un curso.

  • El cambio en la tensión arterial de los pacientes antes y después de administrarles algún fármaco.

Ya has decidido qué prueba t realizar. Los siguientes pasos te dirán cómo calcular el valor p de la prueba t o sus valores críticos, y luego qué decisión tomar sobre la hipótesis nula.

1. Decide la hipótesis alternativa:

   • Utiliza una prueba t de dos colas si solo te importa si la media de la población (o, en el caso de dos poblaciones, la diferencia entre las medias de las poblaciones) coincide o no con un valor preestablecido.

   • Utiliza una prueba t de una cola si quieres comprobar si esta media (o diferencia de medias) es mayor/menor que un valor preestablecido.

2. Calcula el valor de la puntuación t:

   Las fórmulas para el estadístico de contraste en las pruebas t incluyen el tamaño de la muestra, así como su media y desviación estándar. La fórmula exacta depende del tipo de prueba t; dirígete a las secciones específicas para cada prueba para más detalles.

3. Determina los grados de libertad de la prueba t:

   Los grados de libertad son el número de datos de una muestra que son libres de variar a medida que estimamos los parámetros estadísticos. En el caso más sencillo, el número de grados de libertad es igual a tu tamaño de muestra menos el número de parámetros que necesitas estimar. De nuevo, la fórmula exacta depende de la prueba t que quieras realizar; consulta las secciones siguientes para más detalles.

Los grados de libertad son de vital importancia, ya que determinan la distribución que sigue tu puntuación t (bajo la hipótesis nula). Si hay d grados de libertad, la distribución muestral del estadístico de contraste es la distribución t de Student con d grados de libertad. Esta distribución tiene una forma similar a N(0,1) (curva en forma de campana y simétrica), pero tiene colas más gruesas. Si el número de grados de libertad es grande (>30), que generalmente ocurre en muestras grandes, la distribución t de Student es prácticamente indistinguible de N(0,1).

Recuerda que el valor p es la probabilidad (calculada bajo la suposición de que la hipótesis nula es cierta) de que el estadístico de contraste produzca valores al menos tan extremos como la puntuación t producida para la muestra. Como las probabilidades corresponden a áreas bajo la función de densidad, el valor p de la prueba t puede ilustrarse muy bien con la ayuda de las siguientes imágenes:

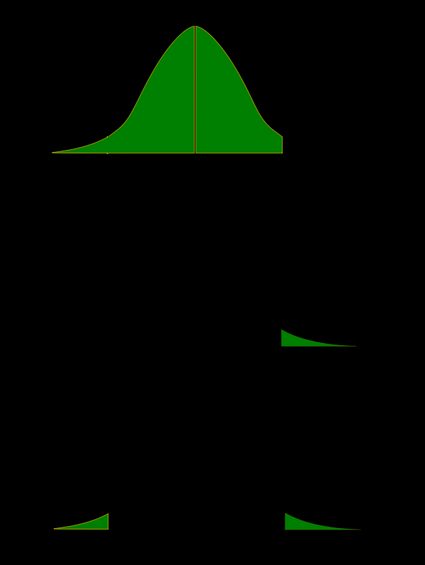
Las fórmulas siguientes indican cómo calcular el valor p de la prueba t. Por FDA_t,d denotamos la función de distribución acumulada de la distribución t de Student con d grados de libertad:

1. Valor p de una prueba t de cola izquierda:

   valor p = FDA_t,d(puntuación t)

2. Valor p de prueba t de cola derecha:

   valor p = 1 − FDA_t,d(puntuación t)

3. Valor p de prueba t de dos colas:

   valor p = 2 × FDA_t,d(-|puntuación t|)

   o, lo que es lo mismo: valor p = 2 − 2 × FDA_t,d(|puntuación t|)

Sin embargo, la FDA de la distribución t viene dada por una fórmula un poco complicada. Para hallar el valor p a mano, tendrías que recurrir a tablas estadísticas, donde se recogen valores aproximados de la FDA, o a software estadístico especializado. Afortunadamente, ¡nuestra calculadora de la prueba t calcula por ti el valor p de la prueba t en un abrir y cerrar de ojos!

Recuerda que al utilizar los valores críticos para probar la hipótesis, tienes que establecer un nivel de significancia, α, antes de calcular los valores críticos, que a su vez dan lugar a regiones críticas (también llamadas regiones de rechazo).

Las fórmulas de los valores críticos emplean la función cuantil de la distribución t, es decir, la inversa de la FDA:

1. Valor crítico para la prueba t de cola izquierda:
   FDA_t,d^-1(α)

   región crítica:

   (-∞, FDA_t,d^-1(α)]

2. Valor crítico para la prueba t de cola derecha:
   FDA_t,d^-1(1-α)

   región crítica:

   [FDA_t,d^-1(1-α), ∞)

3. Valores críticos para la prueba t de dos colas:
   ±FDA_t,d^-1(1-α/2)

   región crítica:

   (-∞, -FDA_t,d^-1(1-α/2)] ∪ [FDA_t,d^-1(1-α/2), ∞)

Para decidir como actuar frente a la hipótesis nula, basta con comprobar si la puntuación t se encuentra dentro de la región crítica:

• Si tu puntuación t pertenece a la región crítica, rechaza la hipótesis nula y acepta la hipótesis alternativa.

• Si tu puntuación t está fuera de la región crítica, entonces no tienes pruebas suficientes para rechazar la hipótesis nula.

1. Elige el tipo de prueba t que deseas realizar:

   • una prueba t de una muestra (para contrastar la media de un único grupo con una media hipotetizada);

   • una prueba t de dos muestras (para comparar las medias de dos grupos); o

   • una prueba t pareada (para comprobar cómo cambia la media de un mismo grupo tras alguna intervención).

2. Decide la hipótesis alternativa:

   • de dos colas;

   • de cola izquierda; o

   • de cola derecha.

3. Esta calculadora de pruebas t te permite utilizar el valor p o las regiones críticas para verificar si se cumple la hipótesis.

4. Introduce la puntuación t y el número de grados de libertad. Si no tienes esos valores, introduce, en cambio, algunos datos sobre la(s) muestra(s): tamaño de la muestra, media y desviación estándar, y nuestra calculadora de pruebas t calculará la puntuación t y los grados de libertad por ti.

5. Una vez que tengas todos los parámetros, el valor p, o región crítica, aparecerá inmediatamente debajo de la calculadora de la prueba t, ¡junto con una interpretación de los resultados!

1. La hipótesis nula es que la media de la población es igual a algún valor $\mu_0$.

2. La hipótesis alternativa es que la media poblacional es

   • diferente de $\mu_0$;
   • menor que $\mu_0$; o
   • mayor que $\mu_0$.

Fórmula de la prueba t de una muestra:

donde:

• $\mu_0$ — la media propuesta en la hipótesis nula;
• $n$ — el tamaño de la muestra;
• $\bar{x}$ — la media muestral; y
• $s$ — la desviación estándar de la muestra.

Número de grados de libertad en la prueba t (una muestra) = $n-1$.

1. La hipótesis nula es que la diferencia entre las medias de estos grupos, $\mu_1$ y $\mu_2$, es igual a algún valor, $\Delta$.

2. La hipótesis alternativa es que la diferencia $\mu_1 - \mu_2$ es:

   • diferente de $\Delta$;
   • menor que $\Delta$; o
   • mayor que $\Delta$.

En particular, si fijamos $\Delta = 0$:

1. La hipótesis nula es que las medias poblacionales son iguales.

2. La hipótesis alternativa es que las medias:

   • $\mu_1$ y $\mu_2$ son diferentes entre sí;
   • $\mu_1$ es menor que $\mu_2$; y
   • $\mu_1$ es mayor que $\mu_2$.

Formalmente, para realizar una prueba t, debemos suponer además que las varianzas de las dos poblaciones son iguales (este supuesto se denomina homogeneidad de varianzas).

Existe una versión de la prueba t que puede aplicarse sin el supuesto de homogeneidad de varianzas: se denomina prueba t de Welch. Para facilitarte las cosas describimos ambas versiones.

Prueba t de dos muestras si las varianzas son iguales

Utiliza esta prueba si sabes que las varianzas de las dos poblaciones son iguales (o muy parecidas).

Fórmula de la prueba t de dos muestras (con varianzas iguales):

donde $s_p$ es la llamada desviación estándar combinada, que calculamos como:

y

• $\Delta$ — la diferencia de medias propuesta en la hipótesis nula;
• $n_1$ — el tamaño de la primera muestra;
• $\bar{x}_1$ — la media de la primera muestra;
• $s_1$ — la desviación estándar de la primera muestra;
• $n_2$ — el tamaño de la segunda muestra;
• $\bar{x}_2$ — la media de la segunda muestra; y
• $s_2$ — la desviación estándar de la segunda muestra.

Número de grados de libertad en la prueba t (dos muestras, varianzas iguales) = $n_1 + n_2 - 2$.

Prueba t de dos muestras si las varianzas son distintas (prueba t de Welch)

Utiliza esta prueba si las varianzas de las poblaciones son diferentes.

Fórmula de la prueba t de Welch de dos muestras si las varianzas son desiguales:

donde

• $\Delta$ es la diferencia de medias propuesta en la hipótesis nula;
• $n_1$ es el tamaño de la primera muestra;
• $\bar{x}_1$ es la media de la primera muestra;
• $s_1$ es la desviación estándar de la primera muestra;
• $n_2$ es el tamaño de la segunda muestra;
• $\bar{x}_2$ es la media de la segunda muestra; y
• $s_2$ es la desviación estándar de la segunda muestra.

El número de grados de libertad en una prueba t de Welch (prueba t de dos muestras con varianzas diferentes) es muy difícil de contar. Podemos aproximarlo con ayuda de la siguiente fórmula de Satterthwaite:

Alternativamente, puedes tomar el menor de $n_1 - 1$ y $n_2 - 1$ como una estimación conservadora del número de grados de libertad.

Como habitualmente realizamos una prueba t pareada cuando tenemos datos sobre unos mismos sujetos medidos dos veces (antes y después de algún tratamiento), nos referiremos a las muestras como pre-grupo y pos-grupo.

1. La hipótesis nula es que la diferencia entre las medias de las poblaciones de ambos grupos es igual a algún valor preestablecido, $\Delta$.

2. La hipótesis alternativa es que la diferencia real entre estas medias es:

   • diferente de $\Delta$;
   • menor que $\Delta$; o
   • mayor que $\Delta$.

Normalmente, establecemos esta diferencia como cero. Entonces podemos reformular las hipótesis de la siguiente manera:

1. La hipótesis nula es que las medias del pre-grupo y el pos-grupo son iguales, es decir, el tratamiento no tiene ningún impacto en la población.

2. Hipótesis alternativa:

   • Las medias del pre-grupo y el pos-grupo son diferentes entre sí (el tratamiento tiene algún efecto);
   • La media del pre-grupo es menor que la media del pos-grupo (el tratamiento aumenta el resultado); o
   • La media del pre-grupo es mayor que la media del pos-grupo (el tratamiento disminuye el resultado).

Fórmula de la prueba t pareada

De hecho, ¡una prueba t pareada es técnicamente lo mismo que una prueba t de una muestra! Veamos por qué. Sean $x_1, ... , x_n$ las observaciones previas y $y_1, ... , y_n$ las observaciones posteriores. Es decir, $x_i, y_i$ son las mediciones antes y después para el i-ésimo sujeto.

Para cada sujeto, calcula la diferencia, $d_i := x_i - y_i$. Todo lo que ocurre a continuación es simplemente una prueba t de una muestra realizada sobre la muestra de las diferencias $d_1, ... , d_n$. Echa un vistazo a la fórmula de la puntuación t:

donde:

• $\Delta$ — la diferencia de medias propuesta en la hipótesis nula;

• $n$ — el tamaño de la muestra de diferencias, es decir, el número de pares;

• $\bar{x}$ — la media de la muestra de diferencias; y

• $s$ — la desviación estándar de la muestra de diferencias.

Número de grados de libertad en la prueba t (pareada): $n - 1$

Utilizamos una prueba Z cuando queremos poner a prueba la media poblacional de un conjunto de datos con distribución normal, que posee una varianza poblacional conocida. Si el número de grados de libertad es grande, la distribución t de Student se aproxima mucho a N(0,1).

Por lo tanto, si hay muchos puntos de datos (al menos 30), puedes reemplazar una prueba t por una prueba Z, y los resultados serán casi idénticos. Sin embargo, para muestras pequeñas que tienen una varianza desconocida, debes optar por la prueba t porque, en tales caso, ¡la distribución t de Student difiere significativamente de la N(0,1)!