Calculadora de prueba Z

Esta calculadora de prueba Z es una herramienta que te ayuda a realizar una prueba Z de una muestra sobre la media de la población. Existen dos formas en las que puedes realizar esta prueba en función de tus necesidades: la prueba Z de dos colas y la prueba Z de una cola. También puedes elegir si la calculadora debe determinar el valor p de la prueba Z o si prefieres utilizar el método del valor crítico.

Sigue leyendo para saber más sobre la prueba Z en estadística y, en particular, cuándo utilizar la prueba Z, cuál es la fórmula de la prueba Z y si debes utilizar la prueba Z o la prueba t. Además, te ofrecemos algunos ejemplos paso a paso de cómo se realiza una prueba Z.

O también puedes consultar nuestra calculadora del estadístico t, donde podrás aprender el concepto de otro estadístico esencial. Si también te interesa la prueba F, consulta nuestra calculadora del estadístico F 🇺🇸.

La prueba Z de una muestra es una de las pruebas paramétricas más populares. La hipótesis nula es que el valor medio de la población es igual a un número dado, $\mu_0$:

Realizamos una prueba Z de dos colas si queremos comprobar si la media de la población no es $\mu_0$:

y una prueba Z de una cola si queremos comprobar si la media de la población es menor/mayor que $\mu_0$:

Analicemos ahora las suposiciones de una prueba Z de una muestra.

Puedes utilizar una prueba Z si tu muestra consta de puntos de datos independientes y:

• los datos están distribuidos normalmente, y conoces la varianza de la población;

  o

• la muestra es grande, y los datos siguen una distribución que tiene una media y una varianza finitas. No necesitas conocer la varianza poblacional.

La razón de que existan estas dos posibilidades es que queremos que el estadístico de contraste siga la distribución normal estándar $\mathrm N(0, 1)$. En el primer caso, se trata de una distribución normal estándar exacta, mientras que en el segundo, lo es aproximadamente, gracias al teorema del límite central.

La pregunta sigue siendo: "¿Cuándo se considera que mi muestra es grande? Pues bien, no existe un criterio universal. En general, cuantos más puntos de datos tengas, mejor funcionará la aproximación. Los libros de estadística recomiendan no tener menos de 50 puntos de datos, mientras que 30 se considera el mínimo indispensable.

Sea $x_1, ..., x_n$ una muestra independiente que sigue la distribución normal $\mathrm N(\mu, \sigma^2)$, es decir, con una media igual a $\mu$, y una varianza igual a $\sigma ^2$.

Planteamos la hipótesis nula, $\mathrm H_0 \!\!:\!\! \mu = \mu_0$.

Definimos el estadístico de contraste, Z, como:

donde:

• $\bar x$ es la media de la muestra, es decir, $\bar x = (x_1 + ... + x_n) / n$;

• $\mu_0$ es la media propuesta en $\mathrm H_0$;

• $n$ es el tamaño de muestra;

• $\sigma$ es la desviación estándar de la población.

En lo que sigue, la mayúscula $Z$ significa el estadístico de contraste (tratado como una variable aleatoria), mientras que la minúscula $z$ denotará un valor real de $Z$, calculado para una muestra dada extraída de N(μ,σ²).

Si se cumple $\mathrm H_0$, entonces la suma $S_n = x_1 + ... + x_n$ sigue la distribución normal, con media $n \mu_0$ y varianza $n^2 \sigma$. Como $Z$ es la normalización (puntuación Z) de $S_n/n$, podemos concluir que el estadístico de contraste $Z$ sigue la distribución normal estándar $\mathrm N(0, 1)$, siempre que $\mathrm H_0$ sea cierta. Por cierto, tenemos la calculadora de puntuación Z por si quieres centrarte solo en este valor.

Si nuestros datos no siguen una distribución normal, o si se desconoce la desviación estándar de la población (y, por tanto, en la fórmula para $Z$ sustituimos la desviación estándar de la población $\sigma$ por la desviación estándar de la muestra), entonces el estadístico de contraste $Z$ no es necesariamente normal. Sin embargo, si la muestra es suficientemente grande, entonces el teorema del límite central garantiza que $Z$ es aproximadamente $\mathrm N(0, 1)$.

En los apartados siguientes, te explicaremos cómo utilizar el valor del estadístico de contraste, $z$, para saber si debes o no rechazar la hipótesis nula. Se pueden utilizar dos métodos para ello: el método del valor p y el método del valor crítico, ¡y cubrimos ambos! ¿Cuál debes utilizar? En el pasado, el enfoque del valor crítico era más popular porque resultaba difícil calcular el valor p a partir de la prueba Z. Sin embargo, con la ayuda de las computadoras modernas, podemos hacerlo con bastante facilidad y con una precisión decente. En general, ¡te recomendamos encarecidamente que indiques el valor p de tus pruebas!

Formalmente, el valor p es el nivel de significación más pequeño con el que podría rechazarse la hipótesis nula. De forma más intuitiva, el valor p responde a las preguntas:
Suponiendo que vivo en un mundo en el que se cumple la hipótesis nula, ¿cuán probable es que el valor del estadístico de contraste sea al menos tan extremo como el valor $z$ que tengo para mi muestra?

Por lo tanto, un valor p pequeño significa que tu resultado es muy improbable según la hipótesis nula, y que hay pruebas sólidas contra la hipótesis nula: cuanto más pequeño es el valor p, más sólidas son las pruebas.

Para hallar el valor p, tienes que calcular la probabilidad de que el estadístico de contraste, $Z$, sea al menos tan extremo como el valor que hemos observado realmente, $z$, siempre que la hipótesis nula sea cierta. (La probabilidad de un suceso calculada bajo la hipótesis de que $\mathrm H_0$ es cierta se denotará como $\small \mathrm{Pr}(\text{evento} | \mathrm{H_0})$) Es la hipótesis alternativa la que determina qué significa más extremo:

1. Prueba z de dos colas: los valores extremos son aquellos cuyo valor absoluto es superior a $|z|$, es decir, los menores que $-|z|$ o mayores que $|z|$. Por tanto, tenemos:

La simetría de la distribución normal da:

2. Prueba z de cola izquierda: los valores extremos son los menores que $z$, entonces

3. Prueba z de cola derecha: los valores extremos son los mayores que $z$, por lo que

Para calcular estas probabilidades, podemos utilizar la función de distribución acumulada, (FDA) de $\mathrm N(0, 1)$, que para un número real, $x$, se define como:

Además, los valores p pueden representarse como el área bajo la función de densidad de probabilidad (FDP) de $\mathrm N(0, 1)$, debido a:

Con todos los conocimientos que has adquirido en la sección anterior, estás preparado para aprender sobre las pruebas z.

1. Prueba Z de dos colas:

Del hecho de que $\Phi(-z) = 1 - \Phi(z)$, deducimos que

El valor p es el área bajo la función de distribución de probabilidad (FDP) tanto a la izquierda de $-|z|$, como a la derecha de $|z|$:

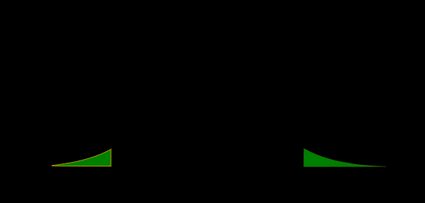
2. Prueba Z de cola izquierda:

El valor p es el área bajo la FDP a la izquierda de nuestro $z$:

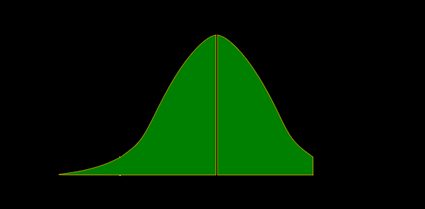
3. Prueba z de cola derecha:

El valor p es el área bajo la FDP a la derecha de $z$:

¡La decisión de rechazar o no la hipótesis nula puede tomarse ahora a cualquier nivel de significación, $\alpha$, que desees!

• si el valor p es menor o igual que $\alpha$, se rechaza la hipótesis nula a este nivel de significación;

• si el valor p es mayor que $\alpha$, entonces no hay pruebas suficientes para rechazar la hipótesis nula en este nivel de significación.

El método del valor crítico consiste en comparar el valor del estadístico de contraste obtenido para nuestra muestra, $z$, con los llamados valores críticos. Estos valores constituyen los límites de las regiones en las que es muy improbable que se encuentre el estadístico de contraste. Esas regiones suelen denominarse regiones críticas, o regiones de rechazo. La decisión de rechazar o no la hipótesis nula se basa entonces en si nuestro $z$ pertenece o no a la región crítica.

Las regiones críticas dependen de un nivel de significación, $\alpha$, de la prueba, y de la hipótesis alternativa. La elección de $\alpha$ es arbitraria; en la práctica, los valores 0.1, 0.05 o 0.01 son los más utilizados como $\alpha$.

Una vez acordado el valor de $\alpha$, podemos determinar fácilmente las regiones críticas de la prueba Z:

1. Prueba Z de dos colas:

Para decidir que pasa con $\mathrm H_0$, comprueba si tu $z$ cae o no en la región crítica:

• en caso afirmativo, rechaza $\mathrm H_0$ y acepta $\mathrm H_1$;

• si la respuesta es negativa, entonces no hay pruebas suficientes para rechazar $\mathrm H_0$.

Como ves, las fórmulas para los valores críticos de las pruebas Z implican la inversa, $\Phi^{-1}$, de la función de distribución acumulada (FDA) de $\mathrm N(0, 1)$.

Nuestra calculadora simplifica los pasos:

1. Elige la hipótesis alternativa: de dos colas o de cola izquierda/derecha.

2. En nuestra calculadora de prueba Z, puedes decidir si utilizas el método del valor p o el de las regiones críticas. En este último caso, establece el nivel de significación, $\alpha$.

3. Introduce el valor del estadístico de contraste, $z$. Si no lo sabes, puedes introducir algunos datos que nos permitan calcular tu $z$ por ti:

   • media muestral $\bar x$ (Si tienes los datos sin procesar, ve a la calculadora de medias para determinar la media);
   • media propuesta $\mu_0$;
   • tamaño de muestra $n$;
   • desviación estándar poblacional $\sigma$ (o desviación estándar muestral si tu muestra es grande).

4. Los resultados aparecen inmediatamente debajo de la calculadora.

Si quieres encontrar $z$ basándote en el valor p, recuerda que en el caso de las pruebas de dos colas hay dos valores posibles de $z$: uno positivo y otro negativo, y son números opuestos. Esta calculadora de prueba Z devuelve el valor positivo en tal caso. Para encontrar el otro valor posible de $z$ para un valor p dado, solo tienes que tomar el número opuesto al valor de $z$ que muestra la calculadora.

Para asegurarnos de que has comprendido bien la esencia de la prueba Z, veamos algunos ejemplos:

1. Una máquina llenadora de botellas sigue una distribución normal. Su desviación típica, declarada por el fabricante, es igual a 30 ml. Un vendedor de zumos afirma que el volumen vertido en cada botella es, en promedio, de un litro, es decir, 1000 ml, pero sospechamos que, en realidad, el promedio es menor que ese...

Formalmente, las hipótesis que establecemos son las siguientes:

• $\mathrm H_0 \! : \mu = 1000 \text{ ml}$

• $\mathrm H_1 \! : \mu \lt 1000 \text{ ml}$

Hemos ido a una tienda y hemos comprado una muestra de 9 botellas. Tras medir cuidadosamente el volumen del contenido de cada botella, hemos obtenido la siguiente muestra (en mililitros):

$\small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980$.

• Tamaño de muestra: $n = 9$;

• Media de la muestra: $\bar x = 980 \ \mathrm{ml}$;

• Desviación estándar de la población: $\sigma = 30 \ \mathrm{ml}$;

• Por lo que

• Y, por tanto, $\text{valor p} = \Phi(-2) \approx 0.0228$.

  Como $0.0228 \lt 0.05$, concluimos que nuestras sospechas no son infundadas; al nivel de significación más común, 0.05, rechazaríamos la afirmación del productor, $\mathrm H_0$, y aceptaríamos la hipótesis alternativa, $\mathrm H_1$.

2. Lanzamos una moneda 50 veces. Obtenemos cruz 20 veces y cara 30. ¿Hay pruebas suficientes para afirmar que la moneda está sesgada?

   Está claro que nuestros datos siguen la distribución de Bernoulli, con una probabilidad de acierto $p$ y una varianza $\sigma^2 = p (1-p)$. Sin embargo, la muestra es grande, por lo que podemos realizar con seguridad una prueba Z. Adoptamos la convención de que obtener cruz es un éxito.

   Formulemos las hipótesis nula y alternativa:

   • $\mathrm H_0 \! : p = 0.5$ (la moneda es justa, la probabilidad de salir cruz es $0.5$)

   • $\mathrm H_1 \! : p \ne 0.5$ (la moneda está sesgada, la probabilidad de cruz difiere de $0.5$)

En nuestra muestra tenemos 20 aciertos (representados por unos) y 30 fallos (representados por ceros), por lo que:

• Tamaño de muestra $n = 50$;

• Media de la muestra $\bar x = 20/50 = 0.4$;

• La desviación estándar de la población viene dada por $\sigma = \sqrt{0.5 \times 0.5}$ (porque $0.5$ es la proporción $p$ hipotetizada en $\mathrm H_0$). Por lo tanto, $\sigma = 0.5$;

• Así que

• Y, por lo tanto,

Desde $0.1573 \gt 0.1$ no tenemos pruebas suficientes para rechazar la afirmación de que la moneda es justa, ni siquiera a un nivel de significación tan grande como $0.1$. En ese caso, puedes utilizar la calculadora de probabilidad de lanzar una moneda para averiguar tus probabilidades de obtener, por ejemplo, 10 caras seguidas (¡que son extremadamente bajas!).