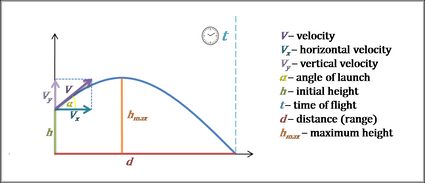
Calculadora de tiro parabólico (movimiento parabólico)

Nuestra calculadora de tiro parabólico es una herramienta que te ayudará a analizar el movimiento parabólico de los proyectiles. Puede hallar el tiempo de vuelo, así como también los componentes de la velocidad, el alcance del proyectil y la altura máxima de la trayectoria. Sigue leyendo si quieres entender qué es un tiro parabólico, familiarizarte con la definición de tiro parabólico y determinar los valores mencionados previamente utilizando las ecuaciones de tiro parabólico.

¿Prefieres ver a leer? Aprende todo lo que necesitas en 90 segundos con este vídeo que hemos hecho para ti:

Imagina que un arquero dispara una flecha al aire. Esta empezará a moverse hacia arriba y hacia adelante, con un cierto ángulo respecto al suelo. Cuanta más distancia cubra, más lento será su ascenso y, eventualmente, descenderá manteniendo su movimiento hacia adelante para finalmente golpear el suelo nuevamente. Si pudieras trazar su trayectoria, sería una curva llamada trayectoria parabólica. Cualquier objeto que se mueva de este modo replica el movimiento parabólico. Por cierto, también tenemos una calculadora de la velocidad de una flecha que analiza el movimiento de las flechas: ¡pruébala!

Sobre un proyectil solo actúa una fuerza: la fuerza de la gravedad. Omitiremos la resistencia del aire. Si dibujaras un diagrama de cuerpo libre de un objeto así, solo tendrías que dibujar un vector que apunte hacia abajo y denotarlo “gravedad”. Si hubiera otras fuerzas actuando sobre el cuerpo, entonces no podríamos llamarlo “un proyectil”.

El movimiento de un proyectil es bastante lógico. Supongamos que conoces la velocidad inicial del objeto $V$, el ángulo en el que sale disparado $\alpha$, y la altura inicial $h$. Nuestra calculadora de tiro parabólico sigue estos pasos para hallar todos los parámetros restantes:

1. Calcula los componentes de la velocidad.

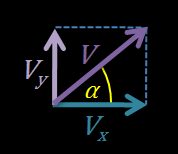
• La componente horizontal de la velocidad $V_\mathrm x$ es igual a $V \cos\alpha$.
• La componente vertical de la velocidad $V_\mathrm y$ es igual a $V \mathrm{sen}\alpha$.
• Los tres vectores —$V$, $V_\mathrm x$ y $V_\mathrm y$— forman un triángulo rectángulo.

Si la componente vertical de la velocidad es igual a 0, entonces es el caso de un tiro horizontal. Si, además, α = 90°, entonces es el caso de caída libre. Abordamos ambos problemas en la calculadora de trayectoria de tiro horizontal 🇺🇸 y en la calculadora de caída libre, respectivamente.

2. Escribe las ecuaciones de movimiento.

Distancia

• La distancia horizontal recorrida puede expresarse como $x = V_\mathrm x t$, donde $t$ es el tiempo.
• La distancia vertical desde el suelo se describe mediante la fórmula $y = h + V_\mathrm{y0} t - g t^2 / 2$, donde $g$ es la aceleración de la gravedad y $V_\mathrm{y0}$ es la velocidad vertical inicial.

Velocidad

• La velocidad horizontal es constante $V_\mathrm x$.
• La velocidad vertical, en cambio, puede expresarse como $V_\mathrm y = V_\mathrm{y0} - g t$.

Aceleración

• La aceleración horizontal es igual a 0.
• La aceleración vertical es igual a $-g$ (porque sobre el proyectil solo actúa la gravedad).

3. Calcula el tiempo de vuelo.

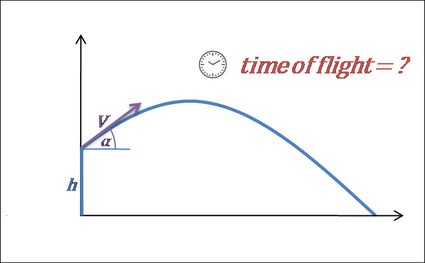
• El vuelo termina cuando el proyectil toca el suelo. Podemos decir que ocurre cuando la distancia vertical al suelo es igual a 0. En el caso de que la altura inicial sea 0, la fórmula puede escribirse como: $V_\mathrm{y0} t - g t^2 / 2 = 0$. Entonces, a partir de esa ecuación, encontramos que el tiempo de vuelo es

• Sin embargo, si estamos lanzando el objeto desde cierta elevación, entonces la fórmula no queda tan compacta como antes, y debemos resolver una ecuación cuadrática: $h + V_\mathrm{y0} t - g t^2 / 2 = 0$. Tras resolver esta ecuación, obtenemos

4. Calcula el alcance del proyectil.

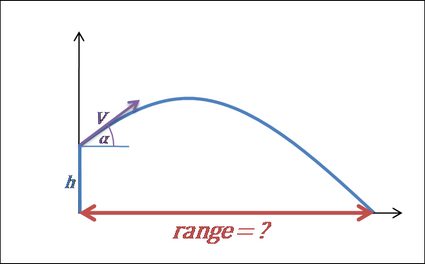
• El alcance del tiro parabólico es la distancia horizontal total recorrida durante el tiempo de vuelo. De nuevo, si lanzamos el objeto desde el suelo (altura inicial = 0), podemos escribir la fórmula como $R = V_\mathrm x t = V_\mathrm x \times 2 \times V_\mathrm{y0} / g$. También podemos transformarlo a $R = V^2_0 \mathrm{sen}(2\alpha) / g$

• Las cosas se complican para una altura inicial distinta de 0. Entonces, tenemos que sustituir la fórmula larga del paso anterior como $t$:

• El alcance es especialmente importante en balística. Hablamos de ello con más detalle en la calculadora de coeficiente balístico 🇺🇸.

5. Calcula la altura máxima.

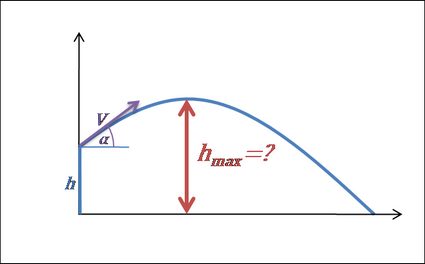
• Cuando el proyectil alcanza la altura máxima, deja de moverse hacia arriba y empieza a caer. Esto significa que su componente de velocidad vertical cambia de positiva a negativa, es decir, es igual a 0 durante un breve instante en el tiempo $t(V_\mathrm y=0)$.
• Si $V_\mathrm {y0} - g t(V_\mathrm y=0) = 0$, entonces podemos reformular esta ecuación a $t(V_\mathrm y=0) = V_\mathrm{y0} / g$.
• Ahora, simplemente hallamos la distancia vertical desde el suelo en ese momento:

• Afortunadamente, en el caso de lanzar un proyectil desde cierta altura inicial $h$, basta con añadir ese valor en la fórmula final:

Uf, ¡han sido muchos cálculos! Resumamos el contenido para tener a mano las ecuaciones del tiro parabólico

1. Lanzando el proyectil desde el suelo (altura inicial h = 0):

• Componente horizontal de la velocidad: $V_\mathrm x = V_0 \cos \alpha$
• Componente vertical de la velocidad: $V_\mathrm y = V_0 \mathrm{sen} \alpha - gt$
• Tiempo de vuelo: $t = 2 V_\mathrm{y0} / g$
• Alcance del proyectil: $R = 2 V_\mathrm x V_\mathrm{y0} / g$
• Altura máxima: $h_\mathrm{máx} = V^2_\mathrm{y0} / (2 g)$

2. Lanzando el objeto desde cierta elevación (altura inicial h > 0):

• Componente horizontal de la velocidad: $V_\mathrm x = V_0 \cos \alpha$
• Componente vertical de la velocidad: $V_\mathrm y = V _0 \mathrm{sen} \alpha - gt$
• Tiempo de vuelo: $t = \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• Alcance del proyectil: $R = V_\mathrm x \left[V_\mathrm{y0} + \sqrt{V^2_\mathrm{y0} + 2 g h}\right] / g$
• Altura máxima: $h_\mathrm{máx} = h + V^2_ \mathrm{y0} / (2 g)$

Utilizar nuestra calculadora de tiro parabólico te ahorrará mucho tiempo. También puede funcionar "a la inversa". Por ejemplo, introduce el tiempo de vuelo, la distancia y la altura inicial, ¡y verás cómo hace todos los cálculos por ti!

No dejes de consultar también la calculadora de parábolas para saber más sobre este tipo de curvas desde un punto de vista matemático.