Calculadora de dirección de un vector

Si quieres calcular la dirección de un vector, estás en el lugar adecuado. Esta calculadora halla el ángulo de la dirección de un vector y calcula un vector unitario 🇺🇸 en esa dirección.

Los vectores son una herramienta poderosa para representar muchas cantidades físicas en nuestro mundo físico. Representan fuerzas, velocidades y muchas otras cantidades derivadas de ellos.

Con esta herramienta, puedes hallar la magnitud y el ángulo de dirección de cualquier vector.

Puedes expresar o calcular la dirección de un vector v de dos formas:

1. Calculando el ángulo de dirección del vector v. El ángulo de dirección es el ángulo que forma v con el eje x positivo, contando en el sentido contrario a las agujas del reloj.
2. Calcula un vector unitario en la dirección del mismo vector. Este vector unitario se llama vector de dirección.

Para calcular el ángulo $\theta$ que forma un vector bidimensional $\vec{v} = (x, y)$ con el eje horizontal, utiliza esta ecuación:

El único problema de esta ecuación es que no nos da el ángulo sobre el eje x positivo, sino sólo sobre el eje horizontal más próximo. Si tu vector se encuentra en el primer cuadrante del plano cartesiano, como el vector que apunta a $P(3, 5)$ en la imagen, no hay problema.

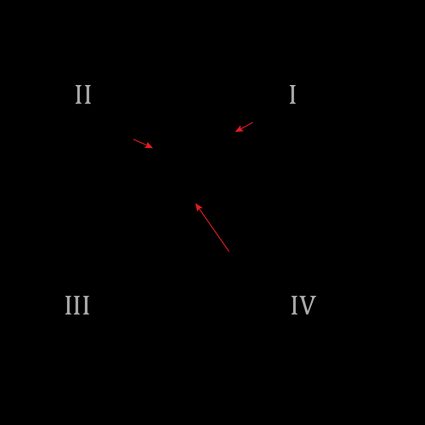
¿Pero qué ocurre si el vector se encuentra en cualquiera de los otros cuadrantes? Supongamos que quieres hallar el ángulo de dirección $\theta$ del vector $Q = (-2, 4)$ de la imagen anterior. Si utilizáramos la fórmula anterior para hallar el ángulo de dirección, no obtendríamos el ángulo correcto, ya que obtendríamos el ángulo $\gamma$ en lugar del ángulo de dirección $\theta$.

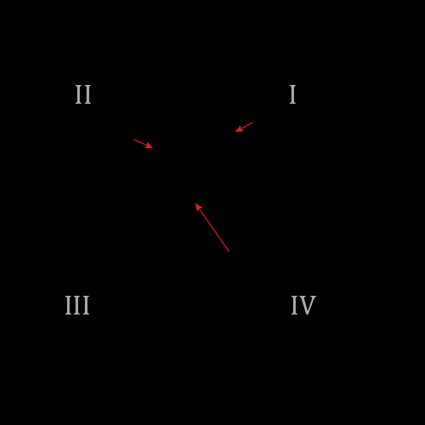
¿Cómo podemos hacer frente a esto? Pues bien, en este caso, podrías haberte dado cuenta de que $\theta = 180^\circ - \gamma$. Podemos extender este razonamiento a los demás casos y llegar a las siguientes ecuaciones para calcular la dirección del vector en cada cuadrante:

• En el primer cuadrante, $\theta_\text{I} = \arctan(\frac{y}{x})$.
• En el segundo cuadrante, $\theta_\text{II} = 180° - \arctan(\frac{y}{x})$.
• En el tercer cuadrante, $\theta_\text{III} = 180° + \arctan(\frac{y}{x})$.
• En el cuarto cuadrante, $\theta_\text{IV} = 360° - \arctan(\frac{y}{x})$.

Para hallar un vector unitario û en la dirección de otro vector v = (x, y, z), sigue estos pasos:

1. Halla la magnitud del vector v:

   |v| = √(x² + y² + z²)

2. Divide cada coeficiente del vector v por la magnitud de v:

   û = v/|v| = (x/|v|, y/|v|, z/|v|)

3. Eso es. û es el vector unitario en la dirección de v.

Encontrar un vector de una magnitud determinada en la dirección de otro vector v = (x, y, z):

1. Halla la magnitud del vector v:

   |v| = √(x² + y² + z²)

2. Encuentra un vector unitario û en la dirección de v. Para ello, divide cada coeficiente del vector v por la magnitud del vector:

   û = v/|v| = (x/|v|, y/|v|, z/|v|)

3. Multiplica la magnitud del vector deseado por el vector unitario û. El resultado será el vector deseado.

Para hallar la magnitud y la dirección de dos vectores, debes hallar el vector resultante (puedes utilizar nuestra calculadora de suma de vectores 🇺🇸 para hacerlo) y aplicarle los pasos descritos anteriormente.

Ahora que ya sabes cómo hallar la magnitud y el ángulo de dirección de un vector, veamos algunos ejemplos numéricos y preguntas frecuentes.