Calculadora del volumen de un prisma triangular

Nuestra calculadora del volumen de un prisma triangular es una herramienta sencilla que puede resolver todas tus dudas relacionadas con el tema, utilizando uno de los 6 métodos disponibles con 6 conjuntos de datos diferentes. 📐

No solo descubrirás cuál es la fórmula del volumen de un prisma triangular, sino que también te explicaremos las matemáticas que la hacen posible.

Prepárate: te ayudaremos a comprender por fin cómo hallar el volumen de un prisma triangular tú solo. 🤓

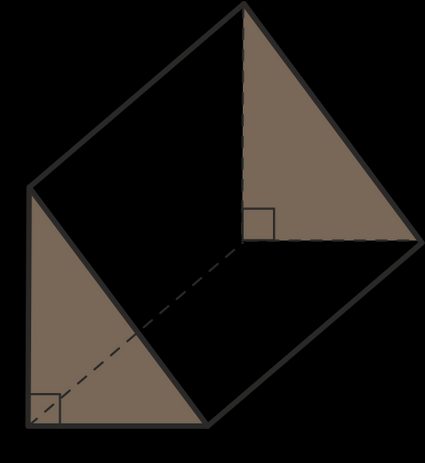
Un prisma triangular es un sólido que se forma al extruir (extender o proyectar) un triángulo en la dirección perpendicular a su superficie. Un prisma triangular es un poliedro con triángulos como bases y rectángulos como caras laterales.

Entonces, ¿cómo hallar el volumen de un prisma triangular con ayuda de nuestra herramienta? Es tan fácil como parece; ¡estás a solo segundos de tu resultado!

1. Selecciona el tipo de cálculo de la cara del triángulo

   Piensa en lo que ya sabes sobre el triángulo presente en el prisma, y averigua qué valores se dan:

   • ▲ Longitud de la base y altura: ya conoces la longitud de la base y la altura del triángulo;
   • ◣ Triángulo rectángulo: tu triángulo tiene un ángulo recto (90°) entre dos de sus brazos. Conoces las longitudes de estos catetos (esta opción sirve como calculadora del volumen de un prisma triangular recto);
   • ▲ 3 lados: conoces las longitudes de los tres lados del triángulo;
   • ▲ 2 lados + ángulo entre ellos: conoces las longitudes de dos lados y el valor del ángulo entre ellos;
   • ▲ 2 ángulos + lado entre ellos: conoces el valor de dos ángulos del triángulo y la longitud del lado que está entre ellos;
   • ▲ Área de la cara triangular: la opción perfecta si vas un paso por delante y ya has calculado el área de una cara triangular de tu prisma.

2. Introduce todos los datos dados en tu consulta

   Puedes elegir entre 11 unidades diferentes, ¡y puedes mezclarlas!

3. Tus resultados están aquí 🎉

No ha estado tan mal, ¿verdad? ¿Qué tal si pruebas nuestras otras calculadoras de prismas?

🔺 Triangulares:

• Calculadora de prismas triangulares;
• Calculadora del área de un prisma triangular.

♦️ Rectangulares:

• Calculadora de prismas rectangulares;
• Calculadora del volumen de un prisma rectangular;
• Calculadora del área de un prisma rectangular.

Como ya hemos dicho, hay 6 formas de averiguar cuál es el volumen de un prisma triangular en nuestra calculadora. Naveguemos rápidamente por todas ellas.

1. ▲ Base y altura

   Esta es la ecuación básica del volumen de un prisma triangular:

   Volumen = 1/2 × Base × Altura × Longitud

   Donde:

   • Base y Altura son los valores de la cara triangular del prisma;
   • Longitud es la longitud de todo el prisma, es decir, la distancia entre dos caras triangulares.

2. ◣ Triángulo rectángulo

   ¡Probablemente el tipo de prisma más popular!

   La fórmula del prisma triangular recto es la siguiente:

   Volumen = Longitud × ((a × b) / 2)

   Donde:

   • a y b son los lados del triángulo que tocan el ángulo recto;
   • Longitud es la longitud de todo el prisma, es decir, la distancia entre dos caras triangulares.

   Para calcular el lado c, puedes usar el teorema de Pitágoras.

3. ▲ 3 lados

   Volumen = 1/4 × √( (a+b+c) × (-a+b+c) × (a-b+c) × (a+b-c) ) × Longitud

   Donde:

   • √ es la raíz cuadrada de la multiplicación de todas las sumas de los lados del triángulo (x² = y, √y = x);
   • a, b y c son los lados de la cara triangular;
   • Longitud es la longitud de todo el prisma, es decir, la distancia entre dos caras triangulares.

4. ▲ 2 lados + ángulo entre ellos

   Volumen = 1/2 × a × b × sen(γ) × Longitud

   Donde:

   • sen(γ) es el seno del ángulo γ (utiliza las tablas de senos y nuestra calculadora de la ley de los senos para comprender la base de esta ecuación);
   • a y b son los lados del triángulo que tocan el ángulo γ;
   • γ: su valor debe estar entre 0 y 180 grados; y
   • Longitud significa la longitud de todo el prisma, es decir, la distancia entre dos caras triangulares

5. ▲ 2 ángulos + lado entre ellos

   Volumen = 1/2 × a ×((a × sen(β))/ sen(β + γ)) × sen(γ) × Longitud

   Donde

   • sen es el seno de un ángulo. Se encuentra con las tablas de senos, basadas en la ley de los senos (como ya se ha mencionado);
   • a es el lado de un triángulo que toca tanto al ángulo γ como al ángulo β;
   • γ; su valor debe estar entre 0 y 180 grados;
   • β; su valor debe estar entre 0 y 180 grados;
   • Longitud; la longitud de todo el prisma, es decir, la distancia entre dos caras triangulares

6. ▲ Área de la cara triangular

   La mejor solución si ya conoces la cara triangular.

   Volumen = Área de la base del triángulo × Longitud

   Donde:

   • El área de la base del triángulo se da en unidad de área, por ejemplo, pulgadas cuadradas (in²), metros cuadrados (m²) o millas cuadradas (mi²);
   • Longitud significa la longitud de todo el prisma, es decir, la distancia entre dos caras triangulares