Calculadora de hexágonos

Bienvenido a la calculadora de hexágonos, una herramienta sumamente útil para realizar cálculos relacionados con hexágonos regulares. El hexágono es una de las formas más comunes en la naturaleza, desde los panales de abejas hasta las baldosas hexagonales para espejos; sus usos son casi infinitos. Aquí explicamos no solo por qué este polígono de seis lados es tan popular, sino también cómo sacar las medidas de un hexágono. Además, respondemos a la pregunta: "¿qué es un hexágono?"

Con nuestra calculadora de hexágonos, podrás explorar diversas propiedades geométricas y hacer cálculos, incluyendo el área de un hexágono. Además, aprenderás la fórmula para sacar el área de un hexágono, regular o no.

Antes de hablar de nuestra calculadora de hexágonos, debemos hablar de qué es un hexágono y cuántos lados tiene. No es de extrañar que el hexágono (también conocido como "polígono de seis lados") tenga exactamente seis lados. Este hecho es cierto para todos los hexágonos, ya que es su característica distintiva. La longitud de los lados puede variar incluso dentro de un mismo hexágono, excepto cuando se trata del hexágono regular, en el que todos los lados deben tener la misma longitud.

Profundizaremos un poco más en esta forma más adelante, cuando abordemos el tema de cómo sacar el área de un hexágono. Por ahora, basta con decir que el hexágono regular es el más común entre los polígonos de seis lados y es el que se encuentra con mayor frecuencia en la naturaleza.

Hemos dedicado una sección entera a las propiedades más importantes del hexágono regular, pero antes, contestemos esta pregunta: "¿Qué es un hexágono?" Responder esto nos ayudará a entender los trucos que podemos utilizar para calcular el área de un hexágono sin utilizar ciegamente la fórmula del área del hexágono. Estos trucos consisten en usar otros polígonos como cuadrados, triángulos e incluso paralelogramos.

Como ya hemos mencionado, el hexágono regular debe tener todos los lados de igual longitud y todos sus ángulos internos deben ser iguales. Cualquier longitud de lado es igualmente válida (¡siempre y cuando sea compartida por los 6 lados!), por lo que calcular el perímetro de un hexágono es tan sencillo que ni siquiera necesitas utilizar la calculadora del perímetro de polígonos regulares 🇺🇸. Solo tienes que calcular:

• perímetro = 6 × lado

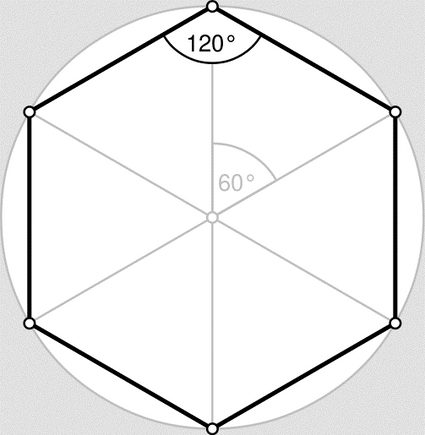
Los ángulos de un hexágono arbitrario pueden tener cualquier valor, pero todos deben sumar 720º (puedes convertirlos fácilmente a otras unidades con nuestra calculadora de conversión de ángulos 🇺🇸). Como el hexágono regular requiere que todos los ángulos sean iguales, se deduce que cada ángulo individual debe medir 120º. Veremos que este hecho es de suma importancia cuando hablamos de la popularidad de la forma hexagonal en la naturaleza. También será útil al explicar cómo calcular el área de un hexágono regular. De igual manera, lo usaremos para obtener la fórmula del área de los hexágonos regulares.

A continuación, veremos cómo sacar el área de un hexágono utilizando diferentes trucos. La forma más sencilla es usando nuestra calculadora de hexágonos, que incluye una herramienta de conversión de áreas. Para aquellos que quieran saber cómo hacerlo manualmente, explicaremos cómo sacar el área de un hexágono regular, tanto con la fórmula del área del hexágono como sin ella.

La fórmula del área de un polígono siempre es la misma, sin importar cuántos lados tenga, siempre y cuando sea un polígono regular:

• área = apotema × perímetro / 2

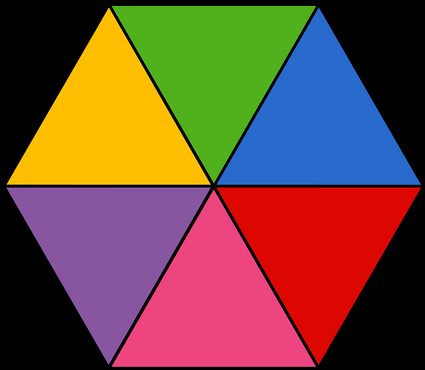
Como recordatorio, la apotema es la distancia entre el punto medio de cualquier lado y el centro de la figura. Puedes visualizarla como la altura del triángulo equilátero que se forma al tomar un lado y dos radios del hexágono (cada una de las áreas coloreadas en la imagen de arriba). Alternativamente, también se puede pensar en la apotema como la distancia entre el centro y cualquier lado del hexágono, ya que la distancia euclidiana se define empleando una línea perpendicular.

Si no recuerdas la fórmula, puedes visualizar el polígono de seis lados como una agrupación de seis triángulos. En el caso del hexágono regular, estos triángulos son equiláteros, lo que simplifica enormemente el cálculo de su área. Comparado con dividirlo en triángulos isósceles o incluso con triángulos 45-45-90, como sucede con un cuadrado, este enfoque resulta mucho más sencillo.

Para el triángulo equilátero, todos los lados tienen la misma longitud, que es la longitud del lado del hexágono que forman. La llamaremos a. La altura del triángulo se puede calcular como h = √3/2 × a, que es el valor exacto de la apotema. Recordemos que √ indica raíz cuadrada. Usando esto, podemos empezar con las matemáticas:

• A₀ = a × h / 2
• = a × √3/2 × a / 2
• = √3/4 × a²

Donde A₀ indica el área de cada uno de los triángulos equiláteros en los que hemos dividido el hexágono. Tras multiplicar esta área por 6 (porque tenemos 6 triángulos), obtenemos la fórmula del área del hexágono:

• A = 6 × A₀ = 6 × √3/4 × a²

• A = 3 × √3/2 × a²

• = (√3/2 × a) × (6 × a)/2

• = apotema × perímetro/2

¡Esperamos que ahora sea más sencillo ver cómo obtener la misma fórmula del área del hexágono que mencionamos anteriormente!

Si quieres ser más creativo, puedes probar con otras formas diferentes. Por ejemplo, supongamos que divides el hexágono por la mitad (de vértice a vértice). En ese caso, obtienes dos trapecios, y puedes calcular el área del hexágono como la suma de ambos. También puedes combinar dos triángulos adyacentes para formar un total de 3 rombos diferentes y calcular el área de cada uno por separado. Incluso puedes descomponer el hexágono en un gran rectángulo (utilizando las diagonales cortas) y 2 triángulos isósceles.

Siéntete libre de jugar con diferentes formas y calculadoras para descubrir qué otros trucos se te ocurren. ¡Puedes intentar usar solo triángulos rectángulos o incluso triángulos rectángulos especiales para calcular el área de un hexágono!

El número total de diagonales del hexágono es igual a 9, 3 de ellas son diagonales largas que cruzan el punto central, y las otras 6 corresponden a la "altura" del hexágono.
Nuestra calculadora de hexágonos también puede simplificar los cálculos de las longitudes de las diagonales. A continuación, te explicamos cómo calcular los dos tipos de diagonales:

• Diagonales largas: siempre cruzan el punto central del hexágono. Como puedes observar en la imagen superior, la longitud de este tipo de diagonales es igual a la longitud de dos aristas:

  D = 2 × a

• Diagonales cortas: no cruzan el punto central. Se construyen uniendo dos vértices, dejando exactamente uno entre ellos. Su longitud es igual a:

  d = √3 × a

Otro par de valores importantes en un hexágono son el circunradio y el inradio. El circunradio es el radio de la circunferencia que contiene todos los vértices del hexágono regular. El inradio es el radio de la circunferencia más grande que cabe completamente dentro del hexágono.

• Circunradio: para sacar el radio de una circunferencia circunscrita en el hexágono regular, hay que determinar la distancia entre el punto central del hexágono (que es también el centro de la circunferencia) y cualquiera de los vértices. Es simplemente igual a R = a.

• Inradio: el radio de un círculo inscrito en el hexágono regular es igual a la mitad de su altura, que es también la apotema: r = √3/2 × a.

Ahora exploraremos un mundo más práctico y menos matemático: cómo dibujar un hexágono. Para un hexágono cualquiera (irregular), la respuesta es sencilla: dibuja cualquier forma de seis lados de modo que sea un polígono cerrado, y ya está. Pero para un hexágono regular, las cosas no son tan fáciles, ya que tenemos que asegurarnos de que todos los lados tengan la misma longitud.

Para obtener un resultado perfecto, necesitarás un compás de dibujo. Dibuja un círculo y, utilizando el mismo radio, comienza a hacer marcas a lo largo de su circunferencia. Empieza en un punto al azar y, usando la marca anterior como punto de apoyo, dibuja un círculo con el compás. Terminarás con 6 marcas. Luego, une las marcas con líneas rectas y obtendrás un hexágono regular. Puedes ver un proceso similar en la animación de arriba.

La calculadora de hexágonos te permite calcular varios parámetros interesantes del hexágono. Esta calculadora es muy fácil de usar, ya que solo necesitas ingresar uno de los parámetros para obtener los demás resultados. Además, incluye una herramienta integrada para convertir unidades de longitud.

Hemos hablado de todos los parámetros de la calculadora, pero para mayor claridad, repasaremos brevemente cada uno de ellos:

• Área del hexágono – Superficie bidimensional encerrada por el hexágono;
• Lado – Distancia de un vértice al siguiente;
• Perímetro – Suma de las longitudes de todos los lados del hexágono;
• Diagonal larga – Distancia de un vértice al opuesto;
• Diagonal corta – Distancia entre dos vértices que tienen otro vértice entre ellos;
• Circunradio – Distancia del centro a un vértice (Igual que el radio del hexágono); y
• Inradio – Igual que la apotema.

A todos nos gusta una buena aplicación en el mundo real, y los hexágonos son sin duda uno de los polígonos más utilizados del mundo. Empezando por los usos humanos, el más sencillo (y probablemente menos emocionante) es el de las baldosas hexagonales para pisos. El hexágono es una forma excelente porque encaja perfectamente entre sí para cubrir cualquier superficie deseada. Si estás interesado en este tipo de aplicación, te recomendamos la calculadora de pisos y la calculadora de baldosas 🇺🇸, ya que son herramientas muy útiles para este propósito.

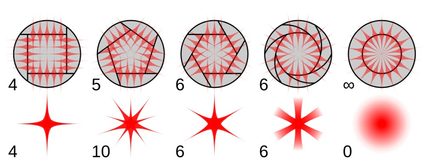
El siguiente caso es común a todos los polígonos, pero sigue siendo interesante de ver. En fotografía, la apertura del sensor casi siempre tiene forma poligonal. Esta parte de la cámara se llama diafragma y dicta muchas propiedades y características de las imágenes producidas por una cámara. La más inesperada es la forma de los objetos muy brillantes (puntiformes) debido al efecto llamado rejilla de difracción, que se muestra en la imagen de arriba.

Uno de los usos más valiosos de los hexágonos en la era moderna, estrechamente relacionado con el que hemos mencionado en fotografía, es en la astronomía. Uno de los mayores problemas que encontramos al observar estrellas lejanas es lo débiles que son en el cielo nocturno. Esto se debe a que, a pesar de ser objetos muy brillantes, están tan lejos que solo nos llega una pequeña fracción de su luz; puedes obtener más información al respecto en nuestra calculadora de luminosidad 🇺🇸. Además, debido a efectos relativistas (similares a la dilatación del tiempo y la contracción de longitud), su luz llega a la Tierra con menos energía de la que fue emitida. Este efecto se conoce como corrimiento al rojo.

El resultado es que obtenemos una cantidad ínfima de energía con una longitud de onda más larga de lo que nos gustaría. La mejor manera de contrarrestarlo es construir telescopios lo más enormes posible. El problema es que fabricar un lente o espejo de una sola pieza de más de un par de metros es casi imposible, por no hablar de los problemas logísticos. La solución es construir un espejo modular utilizando baldosas hexagonales como las que se pueden ver en las imágenes de arriba.

Hacer un espejo tan grande mejora la resolución angular del telescopio, así como el factor de aumento debido a las propiedades geométricas de un "telescopio de Cassegrain". Podríamos afirmar que, gracias a los hexágonos regulares, logramos ver mejor, más lejos y con mayor claridad de lo que jamás podríamos haber hecho con lentes o espejos de una sola pieza.

¿Sabías que también existen los acolchados hexagonales? ¡Descubre más con la calculadora de acolchados hexagonales 🇺🇸 de Omni!

El patrón hexagonal se compone de hexágonos regulares dispuestos uno al lado del otro. Llenan por completo toda la superficie que abarcan, por lo que no hay espacios vacíos entre ellos. Este patrón hexagonal no solo aparece en los panales de miel, sino también en muchos otros lugares de la naturaleza.

Desde las "colmenas" de abejas hasta las grietas de las rocas, pasando por la química orgánica (incluso en los componentes básicos de la vida, como las proteínas), los hexágonos regulares son la forma poligonal más común en la naturaleza. Y hay una razón para ello: los ángulos del hexágono. Mecánicamente, el ángulo de 120º es el más estable de todos, y casualmente es también el ángulo en el que los lados se unen en los vértices cuando alineamos hexágonos uno al lado del otro. Para una descripción completa de la importancia y las ventajas de los hexágonos regulares, recomendamos ver este video.

La forma en que los ángulos de 120º distribuyen las fuerzas (y, a su vez, las tensiones) entre dos de los lados del hexágono lo convierte en una geometría muy estable y mecánicamente eficiente. Esta es una ventaja significativa de los hexágonos. Otra propiedad importante de los hexágonos regulares es que pueden llenar una superficie sin dejar espacios entre ellos (al igual que los cuadrados y triángulos equiláteros). Además, el hexágono regular tiene el menor perímetro para un área dada en comparación con cuadrados y triángulos equiláteros, lo que lo convierte en una opción muy eficiente.

Un ejemplo fascinante que puedes ver en este video es el de las burbujas de jabón. Cuando creas una burbuja utilizando agua, jabón y un poco de aire, esta siempre tiene forma esférica. Este resultado se debe a que el volumen de una esfera es el mayor en comparación con cualquier otro objeto para un área dada.

Sin embargo, cuando colocamos las burbujas juntas sobre una superficie plana, la esfera pierde su ventaja en eficiencia, ya que su sección no puede cubrir completamente un espacio 2D. La siguiente forma más óptima en términos de relación volumen/área, y también la mejor para equilibrar la tensión entre las superficies de las burbujas, es nuestro poderoso hexágono.

Las burbujas son una manera interesante de visualizar las ventajas de un hexágono en comparación con otras formas, pero no es el único ejemplo. En la naturaleza, como hemos mencionado, existen muchos ejemplos de formaciones hexagonales, en su mayoría debidas a esfuerzos y tensiones en los materiales. Desafortunadamente, no podemos revisar todos ellos en detalle. Sin embargo, podemos nombrar algunos lugares en los que se pueden encontrar patrones hexagonales regulares en la naturaleza:

• panales;
• compuestos orgánicos;
• pilas de burbujas;
• formaciones rocosas (como la del Gigante);
• ojos de insectos;
• …