Calculadora de progresiones geométricas

Created by Álvaro Díez and Anna Szczepanek, PhD

Reviewed by Bogna Szyk and Jack Bowater

Translated by Gabriela Diaz and Luis Hoyos

Last updated: Oct 30, 2024

Table of contents:

Calcula todo lo relacionado a una progresión geométrica con nuestra calculadora de progresiones geométricas. Con esta herramienta podrás comprender la definición de progresión geométrica y responder a la pregunta ¿qué es exactamente una progresión geométrica?

Te explicamos la diferencia entre las dos ecuaciones para progresiones geométricas, es decir, la fórmula explícita y la fórmula recursiva. Además, aprenderás cómo aplicar la fórmula de progresión geométrica a través de algunos ejemplos interesantes.

También hemos incorporado una función de “calculadora de series geométricas” que te ayudará a evaluar la suma de una progresión geométrica partiendo de la fórmula explícita de una progresión geométrica y construyendo gradualmente la fórmula de la serie geométrica.

Definición de progresión geométrica

La definición de una progresión geométrica es la siguiente: una sucesión de números, en la que todos, menos el primero, se obtienen multiplicando el anterior por un número fijo, distinto de cero, llamada razón geométrica o factor de la progresión. Si estás teniendo dificultades para entender qué es una progresión geométrica, ¡no te preocupes! Más adelante explicaremos esto de manera más simple y también analizaremos la fórmula recursiva y explícita de una progresión geométrica. También incluimos un par de ejemplos de progresiones geométricas.

Antes de examinar adecuadamente la definición, es importante aclarar algunas cosas para evitar confusiones. En primer lugar, debemos entender que, aunque la progresión geométrica se compone multiplicando constantemente números por un factor, esto no está relacionado con el factorial (ver calculadora factorial 🇺🇸). En realidad, con lo que está relacionado es con el máximo común divisor (MCD) y mínimo común múltiplo (mcm), ya que todos los números comparten un MCD o un mcm si el primer número es un entero.

Esto significa que el MCD (ver calculadora de MCD) es simplemente el número más pequeño de la sucesión. Por el contrario, el mcm es el más grande de los números en la sucesión. Por ejemplo, en la sucesión 3, 6, 12, 24, 48, el MCD es 3 y el mcm sería 48. Pero si consideramos solo los números 6, 12, 24, el MCD sería 6 y el mcm sería 24.

Progresión geométrica: ¿Qué es una progresión geométrica?

Ahora veamos qué es una progresión geométrica en términos sencillos para cualquier persona. Una progresión geométrica es una colección de números concretos que están relacionados por la razón geométrica que hemos mencionado antes. Esta razón geométrica es uno de los rasgos definitorios de una sucesión dada, junto con el término inicial de la sucesión. Más adelante veremos cómo estos dos números están en la base de la definición de la progresión geométrica, y dependiendo de cómo se utilicen, se puede obtener la fórmula explícita para una progresión geométrica o la fórmula recursiva equivalente para la progresión geométrica.

Ejemplos de progresiones geométricas con proporciones de 1/2, 1/3, 1/4 y el término inicial de 1. — Ejemplos de progresiones geométricas con diferentes proporciones

Ahora, construyamos una progresión geométrica sencilla utilizando valores concretos para estos dos parámetros definitorios. Para simplificar las cosas, tomaremos como término inicial $1$ , y la razón geométrica se fijará en $2$ . En este caso, el primer término será $a_1 = 1$ por definición, el segundo término sería $a_2 = a_1 \times 2 = 2$ , el tercer término sería entonces $a_3 = a_2 \times 2 = a_1 × 2^2 = 4$ , etc. El n-ésimo término de la progresión sería entonces:

a_{n} = 1 \times 2^{{n}-1}

donde $n$ es la posición de dicho término en la sucesión.

Como puedes ver, el cociente de dos términos consecutivos cualesquiera de la sucesión —definida igual que en nuestra calculadora de razones— es constante e igual a la razón geométrica.

Una forma habitual de escribir una progresión geométrica es escribir explícitamente los primeros términos. Esto te permite calcular cualquier otro número de la sucesión; para nuestro ejemplo, escribiríamos la serie como:

1, 2, 4, 8, ...

No obstante, existen formas “más matemáticas” de brindar la misma información. Estas otras formas son las conocidas fórmulas explícitas y recursivas para las progresiones geométricas. Ahora que entendemos qué es una progresión geométrica, podemos adentrarnos más en estas fórmulas y explorar maneras de transmitir la misma información con menos palabras y mayor precisión.

Fórmula recursiva frente a fórmula explícita para la progresión geométrica

Existen dos formas diferentes en las que puedes representar matemáticamente una progresión geométrica con solo una fórmula: la fórmula explícita para una progresión geométrica y la fórmula recursiva para una progresión geométrica. La primera de estas es la que ya hemos visto en nuestro ejemplo de serie geométrica. Lo que vimos fue la fórmula específica y explícita para ese ejemplo, pero puedes escribir una fórmula que sea válida para cualquier progresión geométrica, reemplazando los valores de $a_1$ por el término inicial correspondiente y $r$ por la razón geométrica. La fórmula general para el término n-ésimo es:

a_{n} = a_{1}r^{{n}-1}, n \in \mathbb N

donde $n \in \mathbb N$ significa que $n = 1, 2, 3, …$ . La fórmula explícita para las progresiones geométricas transmite la información más importante acerca de una progresión geométrica: el término inicial $a_1$ , cómo obtener cualquier término a partir del primero y el hecho de que no hay término antes del inicial.

La fórmula recursiva consta de dos partes que transmiten información distinta de la definición de progresión geométrica. La primera parte explica cómo llegar de cualquier miembro de la sucesión a cualquier otro miembro empleando la razón geométrica. Este significado por sí solo no es suficiente para construir una progresión geométrica desde cero, ya que no conocemos el punto de partida. Esta es la segunda parte de la fórmula, el término inicial (o cualquier otro término en realidad). Veamos cómo queda esta fórmula recursiva:

\begin{align*} a_{n} &= a_{n-1} r \\ a_{i} &= x \end{align*}

donde $x$ se utiliza para expresar que se utilizará cualquier número en su lugar, pero también que debe ser un número explícito y no una fórmula. El subíndice $i$ indica cualquier número natural (igual que $n$ ), pero se usa en lugar de $n$ para dejar claro que $i$ no tiene por qué ser el mismo número que $n$ .

¿Cómo utilizar la calculadora de progresiones geométricas?

Ahora que sabes qué es una progresión geométrica y cómo escribirla tanto en la fórmula recursiva como en la explícita, ¡es hora de aplicar tus conocimientos y calcular algunas cosas! Con nuestra herramienta, puedes calcular todas las propiedades de las progresiones geométricas, como la razón geométrica, el término inicial, el n-ésimo término, etc. Aquí tienes una breve descripción de cómo está estructurada la calculadora:

Primero, dinos lo que sabes sobre tu progresión eligiendo el valor del Tipo:
- la razón geométrica y el primer término de la sucesión;
- la razón geométrica y algún n-ésimo término; o
- dos términos.
Ingresa tus datos. Basándose en eso, la calculadora determina toda tu progresión geométrica.
Por defecto, la calculadora muestra los primeros cinco términos de tu progresión. Puedes cambiar los términos inicial y final según tus necesidades.

Nuestra herramienta también puede calcular la suma de tu progresión, ya sea toda ella o una parte final. En este último caso, solo necesitas ingresar el punto de inicio y final de la suma, y podrás obtener el resultado. Como aprenderás en las secciones siguientes, ¡la suma infinita puede que no exista!

Fórmula de la serie geométrica: la suma de una progresión geométrica

Hasta ahora hemos hablado de progresiones geométricas, que son conjuntos de números. Sin embargo, hay resultados realmente interesantes que se pueden obtener cuando intentas sumar los términos de una progresión geométrica. Cuando tenemos una progresión geométrica finita, que tiene un número limitado de términos, el proceso es tan sencillo como hallar la suma de una sucesión numérica lineal. Calcular la suma de esta sucesión geométrica puede hacerse incluso a mano, teóricamente.

Pero podemos ser más eficientes que eso utilizando la fórmula de la serie geométrica y experimentando con ella. Para hacer esto, usaremos el signo matemático de sumatoria $\Sigma$ , que significa sumar cada término que sigue. Por ejemplo, si tenemos una progresión geométrica llamada a_n y llamamos S a la suma de la progresión geométrica, la relación entre ambas sería:

\scriptsize S = \sum_{n=1}^m a_{n} = a_{1} + a_{2} + a_{3} + ... + a_m

si queremos sumar los m primeros términos, o:

\scriptsize S = \sum_{n=1}^\infty a_{n} = a_{1} + a_{2} + a_{3} + \ldots

si queremos sumar todos los términos.

Por desgracia, esto aún te deja con el problema de calcular realmente el valor de la serie geométrica. Siempre puedes utilizar esta calculadora como calculadora de series geométricas, pero sería mucho mejor que, antes de utilizar cualquier calculadora de sumas geométricas, comprendieras cómo hacerlo manualmente. Hay un truco que puede facilitarnos mucho el trabajo y consiste en ajustar y resolver la ecuación de la serie geométrica de la siguiente manera:

\scriptsize \begin{align*} S &= \sum_{n=1}^m a_{n} \\ &= a_{1} + a_{1}r + a_{1}r^2 + ... + a_{1}r^{m-1} \end{align*}

Ahora multiplica ambos lados por $(1-r)$ y resuelve:

\scriptsize \begin{align*} S (1 - r) &= (1 - r) (a_1 + a_1r + a_1r^2 + \ldots\\ &\hspace{4em}+\ a_1r^{m-1}) \\[1.5em] \end{align*} \\ \begin{align*} S(1-r) &= a_1 + a_1r + ... + a_1r^{m-1} \\ &\hspace{1em} -(a_1r + a_1r^2 + \ldots + a_1r^{m}) \\[.5em] &= a_1 - a_1r^{m} \end{align*}

\scriptsize S = \sum_{n=1}^m a_{n} = a_1 - a_1 \frac{r^{m}}{1-r} = a_1 \frac{1-r^m}{1-r}

Este resultado es algo que fácilmente puedes calcular por ti mismo, y representa la fórmula básica de la serie geométrica cuando el número de términos en la serie es limitado. Sin embargo, en el mundo de las matemáticas y no en la vida real, podemos tener incluso un número infinito de términos en nuestra serie geométrica y aun así ser capaces de calcular la suma total de todos los términos. ¿Cómo funciona esta magia? No te preocupes, te explicaremos todos los detalles.

Utilizar la fórmula de la progresión geométrica para calcular la suma infinita

Después de ver cómo obtener la fórmula de la serie geométrica para un número finito de términos, es natural (al menos para los matemáticos) preguntarse ¿cómo puedo calcular la suma infinita de una progresión geométrica? Puede parecer imposible hacerlo, pero ciertos trucos nos permiten calcular este valor en unos sencillos pasos. Para ello, necesitamos introducir el concepto de límite. Se trata de un término matemático mediante el cual podemos comprender lo que ocurre en el infinito. También se puede utilizar para intentar definir matemáticamente expresiones que normalmente son indefinidas, como cero dividido por cero o cero a la potencia de cero.

Hablar de límites es un tema muy complejo, y va más allá del alcance de esta calculadora. Su complejidad es el motivo por el que hemos decidido solo mencionarlos y no entrar en detalles sobre cómo calcularlos.

Incluso si no te interesa revisar cuáles son los límites, aún puedes calcular la suma infinita de una serie geométrica usando nuestra calculadora Lo único que debes saber es que no todas las series tienen una suma definida. Las condiciones que debe cumplir una serie para que su suma sea un número (es lo que los matemáticos llaman convergencia), son, en principio, sencillas. Las explicamos en la siguiente sección.

Observaciones sobre el uso de la calculadora como calculadora de series geométricas

Cuando se trata de series matemáticas (tanto geométricas como aritméticas), suelen agruparse en dos categorías diferentes, según si su suma infinita es finita (series convergentes) o infinita / no definida (series divergentes). La mejor forma de saber si una serie es convergente o no es calcular su suma infinita utilizando límites. Si no se puede hacer eso, hay algunos trucos que nos permiten distinguir rápidamente entre series convergentes y divergentes sin tener que hacer todos los cálculos. Estos trucos incluyen: fijarse en el término inicial y general, fijarse en la razón o comparar con otras series.

Visualización de la suma de una progresión geométrica con un término inicial de 1 y un cociente de 1/2 en forma del área de un rectángulo dividido en rectángulos cada vez más pequeños. — Visualización de la suma de una progresión geométrica

Para que una serie sea convergente, el término general $a_n$ tiene que hacerse más pequeño por cada aumento del valor de $n$ . Si $a_n$ disminuye, no podemos garantizar que la serie sea convergente, pero si $a_n$ es constante o aumenta al incrementar $n$ , podemos afirmar con seguridad que la serie será divergente. Si no estamos seguros de si $a_n$ disminuye, podemos fijarnos en el término inicial y en la razón geométrica, o incluso calcular algunos de los primeros términos. Esto nos dará una idea de cómo evoluciona $a_n$ .

La segunda opción que tenemos es comparar la evolución de nuestra progresión geométrica con otra que sepamos con certeza que converge (o diverge), lo que puede hacerse con una rápida búsqueda en línea. Hablando en términos generales, si la serie que estamos investigando es menor (es decir, $a_n$ es menor) que otra que sabemos con seguridad que converge, podemos estar seguros de que nuestra serie también convergerá. Por el contrario, si nuestra serie es mayor que una que sabemos con certeza que es divergente, nuestra serie siempre divergirá. En el resto de los casos (mayor que una convergente o menor que una divergente), no podemos decir nada acerca de nuestra serie geométrica y estamos obligados a encontrar otra serie con la que comparar o a utilizar otro método.

Estos criterios se aplican tanto a las progresiones aritméticas como a las geométricas. De hecho, estas dos están estrechamente relacionadas entre sí y ambas sucesiones pueden vincularse mediante las operaciones de potenciación y de logaritmos.

La paradoja de Zenón y otros ejemplos de sucesiones geométricas

Ya hemos visto un ejemplo de progresión geométrica en forma de la llamada sucesión de potencias de dos. Se trata de una sucesión muy importante debido a las computadoras y su representación binaria de los datos. En esta progresión, podemos encontrar valores como el número máximo permitido en una computadora (varía según el tipo de variable que utilicemos), el número de bytes en un gigabyte, o el número de segundos hasta el final del tiempo UNIX (tanto los valores, original y parcheados).

Además de la sucesión de potencias de dos, podemos tener cualquier otra sucesión de potencias si simplemente sustituimos $r = 2$ con el valor de la base que nos interese. Las series de potencias son comúnmente usadas y ampliamente conocidas, y pueden expresarse empleando la conveniente fórmula de la progresión geométrica. Pero estas sucesiones de potencias no son las únicas sucesiones que podemos tener, y te mostraremos progresiones geométricas aún más importantes o interesantes como la serie alterna o las alucinantes paradojas de Zenón.

Empecemos por las paradojas de Zenón, en particular, la llamada paradoja de la dicotomía. Esta paradoja no es en el fondo más que un rompecabezas matemático en forma de serie geométrica infinita. Zenón fue un filósofo griego anterior a Sócrates. Ideó un mecanismo mediante el cual podía demostrar que el movimiento era imposible y no debía producirse nunca en la vida real. La idea es dividir la distancia entre el punto inicial (A) y el punto final (B) por la mitad. Una vez que hayas recorrido la primera mitad, divides la distancia restante a la mitad nuevamente… Puedes repetir este proceso tantas veces como quieras, lo que significa que siempre te quedará una cierta distancia por recorrer para llegar al punto B.

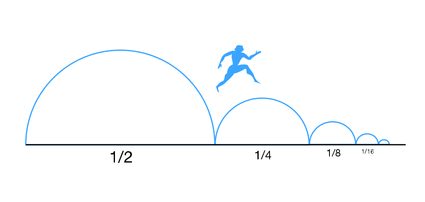
La paradoja de Zenón (dicotomía) visualizada. El velocista griego corre cada vez la mitad de la distancia anterior, con lo que nunca completa la carrera. — Paradoja de Zenón (dicotomía) visualizada

La paradoja de Zenón parece predecir que, dado que tenemos un número infinito de mitades para recorrer, necesitaríamos una cantidad infinita de tiempo para viajar de A a B. Sin embargo, como sabemos por nuestra experiencia cotidiana, esto no es cierto y siempre podemos llegar del punto A al punto B en una cantidad finita de tiempo. La solución a esta aparente paradoja puede encontrarse utilizando las matemáticas.

Si expresamos el tiempo que se tarda en llegar de A a B (llamémoslo por ahora $t$ ) en forma de serie geométrica, tendríamos una serie definida por: $a_1 = t/2$ siendo la razón geométrica $r = 1/2$ . Así, la primera mitad tardaría en recorrerse $t/2$ , luego recorreríamos la mitad de la distancia restante en $t/4$ , luego $t/8$ , etc... Si ahora realizamos la suma infinita de la serie geométrica, encontraríamos que:

\scriptsize\begin{align*} S &= \sum_{n=1}^\infty a_n = \frac{t}{2} + \frac{t}{4} + ... \\[1em] &= t × \left(\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...\right) = t × 1 = t \end{align*}

Esta es la prueba matemática de que podemos ir de A a B en un tiempo finito ( $t$ en este caso).

Para terminar, y por si la paradoja de Zenón no fuera suficientemente alucinante, mencionemos la serie unitaria alternante.

Esta serie comienza en $a_1 = 1$ y tiene una razón geométrica $r = -1$ que da lugar a una serie de la forma

\scriptsize S = \sum_{n=1}^\infty a_n = 1 - 1 + 1 - 1 + ...

Esto no converge según los criterios estándar, porque el resultado depende de si tomamos un número par ( $S = 0$ ) o impar ( $S = 1$ ) de términos. Hay un truco mediante el cual, sin embargo, podemos "hacer" que esta serie converja a un número finito. El truco en sí es muy sencillo, pero está basado en argumentos matemáticos (e incluso metamatemáticos) muy complejos, por lo que si alguna vez se lo enseñas a un matemático te arriesgas a meterte en un buen lío. Estás avisado. Veamos la "solución":

\scriptsize S = 1 - 1 + 1 - 1 + ...

Multiplicamos ambos lados por $-1$ :

\scriptsize\begin{align*} -S &= -1 + 1 - 1 + 1 - ... \\[1em] &= -1 + (1 - 1 + 1 - 1 + ...) \\[1em] &= -1 + S \end{align*}

Si ahora resolvemos $S$ :

\scriptsize -S - S = -1 → 2S = 1 → S = 1/2

Ahora puedes ir y presumir ante tus amigos, siempre que no sean matemáticos.

FAQ

¿Qué es una progresión geométrica?

Una progresión geométrica es una serie de números tal que el término siguiente se obtiene multiplicando el término anterior por un número común.

¿Cómo hallar la suma de una progresión geométrica?

Para hallar la suma de una progresión geométrica:

Calcula la razón geométrica, r elevada a la potencia n.
Resta la resultante rⁿ de 1.
Divide el resultado entre (1 - r).
Multiplica por el primer término, a₁.

¿Cómo hallar el e-nésimo término de una progresión geométrica?

Para hallar el e-nésimo término de una progresión geométrica:

Calcula la razón geométrica elevada a la potencia (n-1).
Multiplica la resultante por el primer término, a.

¿Cómo calcular la razón geométrica de una progresión geométrica?

Para calcular la razón geométrica de una progresión geométrica, divide dos términos consecutivos cualesquiera de la progresión.

Álvaro Díez and Anna Szczepanek, PhD

Formula to find the n-th term of the geometric sequence:

Type

Common ratio r

a₁

Here's your sequence

Starting from term no.

Up to term no.

a₁ =

a₂ =

a₃ =

a₄ =

a₅ =

Summing the sequence

Find

a₁ + a₂ + a₃ + ... =

To increase the precision of calculations, go to the advanced mode.

Arithmetic sequenceCollatz conjectureConvolution… 7 more