Notre calculateur de distance entre deux points permet de trouver rapidement la distance entre deux points quelconques situés dans un plan bidimensionnel.
Dans ce court texte, nous aborderons quelques points importants.
- Comment trouver la distance entre deux points ?
- Comment utiliser la formule de distance entre deux points ?
- Quelle est la plus courte distance entre deux points ?
Commençons !
Vous êtes plutôt du genre à regarder une vidéo que de lire un pavé ? Apprenez tout ce qu'il vous faut en 90 secondes grâce à cette vidéo que nous avons créée pour vous :
Définition de la distance entre deux points : qu'est-ce que la distance ?
D'après sa définition la plus simple, la distance entre deux points dans un plan bidimensionnel, c'est-à-dire dans un système de coordonnées en deux dimensions, est la longueur du segment qui les relie.
Par exemple, si nous plaçons les points et dans un plan bidimensionnel, que nous traçons un segment entre eux et que nous mesurons la longueur de ce segment, nous obtiendrons comme résultat.
Cette définition est dérivée de la définition de distance euclidienne. Celle-ci peut également être définie dans une, trois, quatre ou plus dimensions.
Bien entendu, il n'est pas pratique de tracer et de mesurer des segments chaque fois que l'on veut trouver la distance entre deux points. C'est là qu'intervient la formule de la distance entre deux points.
Formule de la distance entre deux points
Nous pouvons obtenir la définition mathématique de distance à partir de la formule de la distance euclidienne dans un système de coordonnées en deux dimensions :
où :
- et – les coordonnées de l'un des deux points
- et – les coordonnées de l'autre point
- – la distance entre les deux points
💡 C'est cette définition qui fait que la distance la plus courte entre deux points dans un plan bidimensionnel est toujours un segment ! Ne vous inquiétez pas : nous ne nous attarderons pas davantage sur les définitions mathématiques dans ce calculateur de distance entre deux points 😉.
Autres calculateurs utiles
Si vous avez apprécié ce calculateur de distance entre deux points et que vous souhaitez en savoir plus sur d'autres définitions de la distance, consultez l'un de nos autres outils de calcul de distance :
🙋 Essayez-le ! Saisissez les coordonnées de deux points quelconques dans le calculateur de distance entre deux points, et la distance sera affichée automatiquement.
FAQ
Quelle est la distance la plus courte entre deux points ?
La distance la plus courte entre deux points est le segment qui les relie. Cette définition ne s'applique qu'aux surfaces planes ou aux espaces. Si l'on considère une sphère, par exemple, la distance la plus courte entre deux points appartenant à la sphère est un arc appelé distance du grand cercle.
Quelle est la distance entre (5, 10) et (8, 9) ?
3,162 28. Nous pouvons trouver la distance entre les points (5, 10) et (8, 9) en les remplaçant dans la formule de distance entre deux points :
√[(8 - 5)² + (9 - 10)²] = 3,162 28
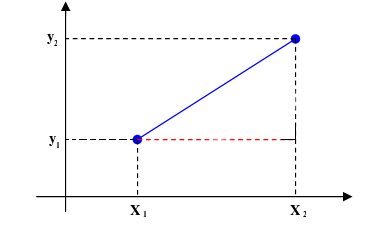
Comment trouver la distance entre deux points ?
Pour trouver la distance entre deux points, il suffit de suivre quelques étapes :
Trouvez les coordonnées du premier point, (x₁, y₁). Peu importe le point choisi tant que l'on ne mélange pas les systèmes de coordonnées.
Trouvez les coordonnées de l'autre point, (x₂, y₂).
Remplacez ces valeurs dans la formule de distance entre deux points :
√[(x₂ - x₁)² + (y₂ - y₁)²]