Calculateur de fraction
Bienvenue sur notre calculateur de fraction. Cet outil polyvalent peut :
- ➕ additionner ;
- ➖ soustraire ;
- ✖️ multiplier ; et
- ➗ diviser deux fractions quelconques.
En outre, il est capable de simplifier une fraction (c'est-à-dire de la réduire) et de vous indiquer comment transformer une fraction en un nombre décimal, et vice versa. Si vous n'êtes toujours pas impressionné·e, sachez que cet outil fonctionne non seulement pour les fractions propres et impropres, mais aussi pour les nombres fractionnaires. Que demander de plus ? 😁
Comme d'habitude, nous avons préparé quelques paragraphes introductifs qui vous permettront de vous plonger dans le monde des fractions 🌎. Vous trouverez ci-dessous la définition des fractions, les types de fractions (propres, impropres, nombres fractionnaires) et toutes les opérations de base sur les fractions. Êtes-vous prêt·e ?
Définition d'une fraction : qu'est-ce qu'une fraction ?
Une fraction représente le nombre de parts égales d'un tout.
Vous pouvez reconnaître une fraction simple parce qu'elle comporte deux nombres séparés par une barre verticale ou oblique.
-
Nous appelons le chiffre du haut le numérateur et nous l'écrivons au-dessus de la barre. Il nous indique :
le nombre de parts que nous avons.
-
Nous appelons le nombre du bas dénominateur et le notons sous la barre. Il nous indique :
le nombre total de parts.
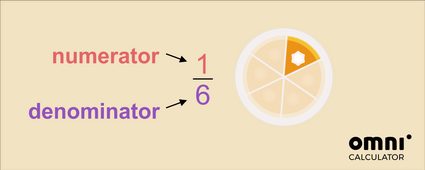
Dans l'exemple ci-dessus, la fraction représente une part sur les six parts que compte la tarte au total. Nous lisons cela comme un sixième de la tarte entière.
Mais, bien sûr, la tarte peut être coupée différemment !
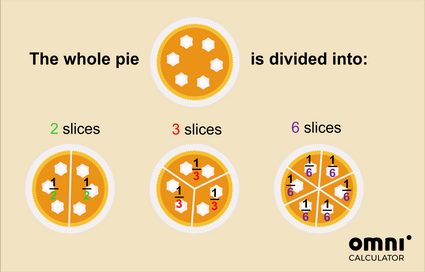
Ainsi, si vous coupez la tarte en 2, une part correspond à la moitié du tout. Si vous coupez la tarte en 3, une part correspond à un tiers de la tarte, etc.
Les fractions sont utilisées tout autour de nous.
-
Chaque fois que vous voulez exprimer une partie d'un élément entier, qui peut être divisé en morceaux égaux : comme un gâteau 🍰, une tablette de chocolat 🍫, une pastèque 🍉, une pizza 🍕, etc.
-
Lorsque nous mesurons quelque chose. 📏
-
La taille de l'écran de votre ordinateur 🖥️ est exprimée sous forme de ratio, par exemple 16:9. Il s'agit également d'une fraction, simplement écrite d'une manière différente. (Pour savoir comment simplifier les ratios, consultez notre calculateur de ratio !)
Qu'est-ce qu'une fraction propre, impropre ou un nombre fractionnaire ?
Maintenant que vous savez ce qu'est une fraction, voyons quels sont les différents types de fractions. En général, il existe trois types de fractions : les fractions propres, les fractions impropres et les nombres fractionnaires.
-
Fractions propres
Dans les fractions propres, le nombre du haut (numérateur) est plus petit que le nombre du bas (dénominateur). Cela signifie que la fraction sera toujours inférieure à l'ensemble.
🍰 5 parts de gâteau sur un gâteau qui a été coupé en 6.
🍫 2 rangées d'une tablette de chocolat sur l'ensemble de la barre de chocolat, qui comporte 5 rangées.
🍊 7 quarts d'une orange que nous avons coupée en 8.
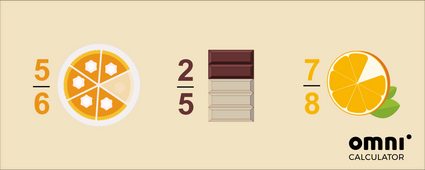
La règle générale, qui s'applique aussi bien aux nombres positifs que négatifs, est que la valeur absolue de la fraction est inférieure à un :
-
Fractions impropres
Qu'est-ce qu'une fraction impropre ? Il s'agit d'une fraction dont le numérateur est supérieur (ou égal) au dénominateur. Voici quelques exemples de fractions impropres !
🍰 10 parts de gâteau, alors que chaque gâteau comporte 6 parts.
🍫 8 rangées d'une tablette de chocolat. Une tablette de chocolat a 5 rangées en tout.
🍊 21 quarts d'orange, si l'on coupe chaque orange en 8 morceaux égaux.

-
Nombres fractionnaires
Les nombres fractionnaires sont une autre façon d'exprimer une fraction impropre. Il s'agit de nombres entiers et d'une fraction propre réunis. Nous allons donc jeter un coup d'œil aux exemples du paragraphe précédent.
🍰 10 parts de gâteau, quand chaque gâteau a 6 parts est la même chose que → 1 gâteau entier et 4 parts sur 6.
🍫 8 rangées de chocolat lorsque la tablette de chocolat entière comporte 5 rangées → 1 tablette de chocolat entière et 3 rangées sur 5.
🍊 21 quarts d'orange, si on coupe l'orange en 8 quarts → 2 oranges entières et 5 quarts sur 8.

💡 Les choses les plus importantes à retenir :
- une fraction propre a un numérateur plus petit que son dénominateur ;
- le numérateur d'une fraction impropre est plus grand (ou égal) que son dénominateur ; et
- un nombre fractionnaire est constitué d'un nombre entier et d'une fraction propre.
➕ Règles d'addition des fractions : comment additionner des fractions ?
Lorsqu'il s'agit d'additionner des fractions, trois cas de figure se présentent :
-
Le dénominateur (nombre du bas) est le même dans les deux fractions, par exemple, 3/5 et 1/5.
C'est le cas le plus simple ; il suffit d'additionner les numérateurs (chiffres du haut) et de laisser le dénominateur tel quel, par exemple :
➽ 3/5 + 1/5 = (3 + 1)/5 = 4/5
-
Les fractions ont des dénominateurs différents, par exemple, 2/5 et 3/10.
Ce cas est un peu plus compliqué : pour additionner ces fractions, vous devez trouver le dénominateur commun.
-
Vous pouvez utiliser, par exemple, le plus petit commun multiple (PPCM) pour trouver le nombre en commun de vos deux dénominateurs :
PPCM(5,10) = 10. Une autre option consiste à multiplier vos dénominateurs et à réduire la fraction par la suite. -
Ensuite, vous devez développer chaque fraction de manière à ce que le dénominateur commun soit le nombre inférieur.
Ainsi, vous devez multiplier la fraction dont le dénominateur est égal à 5 (notre 1/5) par 2 pour obtenir 10 (rappelez-vous que vous devez multiplier les deux nombres du haut et du bas) :
➽ 2/5 = (2 × 2)/(5 × 2) = 4/10
Votre deuxième fraction a déjà un dénominateur égal à 10 :
➽ 3/10
-
Maintenant que vos fractions ont le même dénominateur, vous pouvez les additionner :
➽ 4/10 + 3/10 = (4 + 3)/10 = 7/10
-
-
Vous voulez additionner deux nombres fractionnaires, par exemple, 2 3/5 et 1 1/2.
Une solution pour ce type de problème consiste à convertir le nombre fractionnaire en fraction impropre et à l'additionner comme d'habitude.
Convertissons-la en 2 3/5.
-
Multipliez le nombre entier par le dénominateur :
2 × 5 = 10
-
Ajoutez le résultat à votre numérateur :
10 + 3 = 13
-
C'est votre nouveau numérateur, écrivez-le au-dessus de votre dénominateur :
2 3/5 = 13/5
De manière analogue, vous pouvez trouver que 1 1/2 = 3/2.
-
Effectuez l'addition standard des fractions avec des dénominateurs différents :
➽ 13/5 + 3/2 = 26/10 + 15/10 = 41/10
-
Enfin, vous pouvez reconvertir votre résultat en un nombre fractionnaire.
Effectuez une longue division avec un reste :
➽ 41/10 = 4 R 1 = 4 1/10
-
Bien entendu, notre calculateur de fractions traite tous ces cas de figure. 😎
Si vous vous demandez toujours comment fonctionne l'addition de fractions, peut-être que cette image vous aidera ?
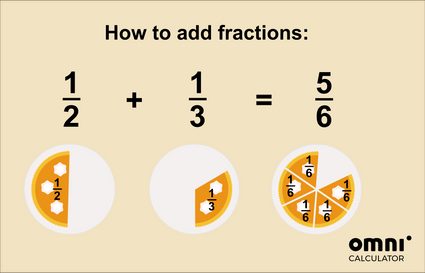
Pour une explication encore plus complète, consultez notre calculateur d'addition de fractions 🇺🇸.
➖ Règles de soustraction des fractions : comment soustraire des fractions ?
Si vous vous demandez comment soustraire des fractions et que vous avez lu la section précédente Comment additionner des fractions, nous avons une bonne nouvelle pour vous : c'est à peu près la même chose !
-
Si vous avez des fractions avec le même dénominateur, soustrayez les numérateurs :
➽ 3/5 - 1/5 = (3 - 1)/5 = 2/5
-
Lorsque vous soustrayez des fractions avec des dénominateurs différents (2/5 et 3/10) répétez la procédure de la section précédente, mais en procédant à une soustraction et non à une addition lors de la dernière étape.
-
Trouvez un dénominateur commun, ici 10.
-
Développez les fractions en fractions équivalentes avec un dénominateur commun : 4/10 et 3/10.
-
Soustrayez les numérateurs :
➽ 2/5 - 3/10 = 4/10 - 3/10 = 1/10
-
-
Pour les nombres fractionnaires (23/5 et 1 1/2).
-
Transformez les nombres fractionnaires en fractions impropres, comme précédemment :
2 3/5 = 13/5 et 1 1/2 = 3/2
-
Soustrayez les deux fractions impropres aux dénominateurs différents :
➽ 13/5 - 3/2 = 26/10 - 15/10 = 11/10
-
Laissez le résultat en une fraction impropre, ou reconvertissez-le en nombre fractionnaire :
➽ 11/10 = 1 R 1 = 1 1/10
-
Vous pouvez imaginer la soustraction comme le fait de prendre ou de manger une partie du gâteau :
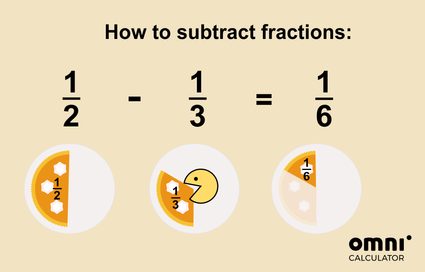
Ce n'était pas si difficile, n'est-ce pas ?
✖️ Règles de multiplication des fractions : comment multiplier des fractions ?
Multiplier des fractions est heureusement une opération qui se fait sans effort. Il suffit de faire : numérateur fois numérateur sur dénominateur fois dénominateur. Parfois, vous devez également simplifier la fraction. Et le tour est joué !
Jetez un coup d'œil à cet exemple :
➽ 2/3 × 5/6 = (2 × 5)/(3 × 6) = 10/18
Vous pouvez ensuite simplifier le résultat en 5/9.
Chaque fois que vous avez affaire à des nombres factionnaires, n'oubliez pas que vous devez toujours les écrire sous forme de nombre impropre avant de les multiplier :
➽ 2 1/2 × 3 1/4 = 5/2 × 13/4 = (5 × 13)/(2 × 4) = 65/8 = 8 1/8
Et lorsque vous multipliez une fraction par un nombre entier, n'oubliez pas que vous pouvez écrire le nombre entier comme lui-même divisé par 1 :
➽ 3 × 5/7 = 3/1 × 5/7 = (3 × 5)/(1 × 7) = 15/7
Si vous ne savez pas comment réduire des fractions, allez à la section Comment simplifier les fractions.
Maintenant que vous savez comment multiplier les fractions, passons au sujet suivant : la division de fractions.
➗ Règles de division des fractions : comment diviser des fractions ?
Vous vous creusez la tête pour savoir comment diviser des fractions ? Pas de soucis ! La division de fractions est assez similaire à la multiplication de fractions. La seule différence est que vous devez multiplier votre premier nombre par l'inverse de la deuxième fraction. Cela peut sembler un peu bizarre, mais c'est très simple ! Regardez cet exemple :
(1/2) / (3/5) = 1/2 × 5/3 = (1 × 5)/(2 × 3) = 5/6
Il vous suffit donc de retourner la deuxième fraction à l'envers (qui est son inverse) et de multiplier les fractions. Parfois, vous devrez également procéder à une réduction des fractions. Et c'est tout, tadaaa ! 🎉
Comment convertir un nombre décimal en fraction ?
Si vous voulez savoir comment convertir un nombre décimal en fraction, vous êtes au bon endroit. Voici un guide étape par étape :
Supposons que vous souhaitiez convertir 0,32 en fraction :
-
Traitez votre partie décimale comme un numérateur. Le dénominateur sera alors 1.
-
Déplacez la virgule vers la droite, jusqu'à ce que vous n'ayez plus qu'un nombre entier :
0,32 → 3,2 → 32
Chaque déplacement correspond à une multiplication par 10.
0,32 × 10 → 3,2 × 10 → 32
-
Vous avez multiplié le numérateur par 10 × 10, et il faut maintenant multiplier le dénominateur par le même nombre :
1 × 10 × 10 = 100
-
Vous avez transformé votre fraction en décimale ! ✨ 0,32 → 32/100
-
Enfin, simplifiez le résultat. Le plus grand commun diviseur de 32 et 100 étant 4, divisez le numérateur et le dénominateur par cette valeur :
➽ 32/100 = 8/25
Et voilà, la fraction sous sa forme la plus simple. ❤️
Comment transformer une fraction en un nombre décimal ?
Eh bien, la façon la plus simple de transformer une fraction en un nombre décimal est… d'utiliser un calculateur. Qu'il s'agisse de ce calculateur de fraction, d'une calculatrice de poche, ou de notre convertisseur de fraction en nombre décimal 🇺🇸.
Parfois, la fraction est relativement facile à convertir en nombre décimal sans aucun outil : comme pour 1/2, 3/4 (ou même 1/8). Nous pensons que vous pouvez trouver comment développer les fractions ci-dessus pour qu'elles aient respectivement 10, 100, 1 000, et ainsi de suite au dénominateur.
-
Multipliez 1/2 par 5 pour obtenir 10 au dénominateur :
➽ 1/2 = 5/10 = 0,5
-
Multipliez 3/4 par 25 pour obtenir 100 au dénominateur :
➽ 3/4 = 75/100 = 0,75
-
Multipliez 1/8 par 125 pour obtenir 1 000 au dénominateur :
➽ 1/8 = 125/1 000 = 0,125
Mais que se passe-t-il si vous n'avez ni Internet ni calculatrice sur vous, mais seulement un stylo et du papier📝 ? Et que votre fraction ne semble pas aussi simple à développer que nos exemples ? Dans ce cas, vous devrez probablement faire la longue division jusqu'aux décimales à la main. Bonne chance ! 🤞
Comment additionner des fractions dont les dénominateurs sont différents ?
Vous devez d'abord trouver un dénominateur commun. Nous utiliserons 1/2 et 3/5 comme exemple. Suivez ces étapes pour additionner des fractions ayant des dénominateurs différents :
-
Trouvez le plus petit commun multiple (PPCM) du dénominateur : 10.
-
Divisez le PPCM par chaque dénominateur et multipliez les numérateurs par la réponse :
-
10/2 = 5
5 × 1 = 5 -
10/5 = 2
2 × 3 = 6
-
-
Additionnez les nombres trouvés à l'étape 2 et placez le résultat au-dessus du PPCM :
-
6 + 5 = 11
-
11/10 = 1 1/10
-
-
Voilà, c'est tout ! Vous avez additionné vos fractions.
Une fraction est-elle un nombre rationnel ?
Oui, toute fraction est un nombre rationnel, mais tous les nombres rationnels ne sont pas des fractions. Un nombre rationnel est une fraction uniquement lorsque le numérateur et le dénominateur sont des nombres entiers.
Comment écrire 0,333 3 sous forme de fraction ?
0,333 3 écrit sous forme de fraction est égal à 3 333/10 000.
Pour trouver cette réponse :
-
Écrivez la partie décimale au numérateur et 1 au dénominateur :
0,333 3/1
-
Déplacer la virgule vers la droite à la fin du nombre pour qu'il apparaisse comme un entier :
3 333
-
Ajoutez le même nombre de zéros au dénominateur que le nombre de rangs dont vous avez déplacé la virgule. Dans le cas présent, il s'agit de quatre :
10 000
-
Placez le nombre de l'étape 2 comme numérateur et le nombre de l'étape 3 au dénominateur :
3 333/10 000
Quel est le produit de 1/2 et de 5/3 ?
Le produit de 1/2 et 5/3 est 5/6.
Pour arriver à cette réponse, nous multiplions les numérateurs et les dénominateurs selon les étapes suivantes :
-
1 × 5 = 5
-
2 × 3 = 6
Donc :
- 1/2 × 5/3 = 5/6
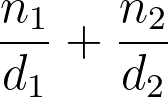
Comment simplifier les fractions ?
Nous aimons toujours nous simplifier la vie, même en mathématiques. C'est pourquoi il est important de simplifier les fractions. Cela signifie que nous écrivons la fraction sous sa forme la plus simple possible. Les fractions simplifiées sont également appelées fractions irréductibles.
Mais qu'est-ce que cela signifie exactement ? Regardez ces exemples !
Pour simplifier une fraction, vous pouvez utiliser deux méthodes :
Utiliser une sorte d'approche à tâtons : diviser la fraction par 2, 3, 5, 7, 11... jusqu'à ce qu'il soit impossible de poursuivre la division (sans reste) :
➽ 42/126 = /:2
➽ 21/63 = /:3
➽ 7/21 = /:7
➽ 1/3
Trouvez le PGCD, le plus grand commun diviseur du numérateur et du dénominateur, puis divisez-les par ce nombre :
PGCD(42,126) = 42, donc :➽ 42/126 = /:42
➽ 1/3
Pour en savoir plus sur la réduction des fractions, consultez notre calculateur de simplification de fractions 🇺🇸. Assurez-vous également de jeter un coup d'œil à notre incroyable calculateur de fractions équivalentes 🇺🇸, qui peut trouver de nombreux équivalents à votre fraction.