Calculateur de racine carrée

Notre calculateur de racine carrée détermine la racine carrée de n'importe quel nombre positif de votre choix. Entrez simplement le nombre que vous souhaitez et le résultat s'affiche automatiquement. Avec cet outil, vous pouvez également estimer le carré du nombre souhaité (il suffit d'entrer la valeur dans le deuxième champ), ce qui peut être d'une grande aide pour trouver des carrés parfaits à partir de la formule de la racine carrée.

Vous avez des difficultés avec les opérations arithmétiques de base : ajouter des racines carrées, soustraire des racines carrées, multiplier des racines carrées ou diviser des racines carrées ? Vous n'avez plus besoin de vous en préoccuper ! Dans le texte suivant, vous trouverez une explication détaillée, avec de nombreux exemples, des différentes propriétés des racines carrées, telles que comment simplifier les racines carrées. Avec cet article, vous apprendrez une fois pour toutes à trouver n'importe quelles racines carrées !

Vous êtes-vous déjà demandé quelle était l'origine du symbole de la racine carrée √ ? Nous pouvons vous assurer que cette histoire n'est pas aussi simple que vous pourriez le penser de prime abord. L'origine du symbole de la racine remonte à l'Antiquité, comme l'origine du pourcentage.

Si vous cherchez le graphique de la racine carrée ou les propriétés de la fonction racine carrée, dirigez-vous directement vers la section appropriée (il suffit de cliquer sur les liens ci-dessus !). Nous y expliquons ce qu'est la dérivée d'une racine carrée à l'aide d'une définition fondamentale de la racine carrée ; nous expliquons également comment calculer les racines carrées d'exposants ou les racines carrées de fractions. Enfin, si vous êtes suffisamment persévérant·e, vous découvrirez que la racine carrée d'un nombre négatif est, en fait, possible. Nous introduisons ainsi les nombres complexes qui trouvent de nombreuses applications en physique et en mathématiques.

L'opération de la racine carrée d'un nombre était déjà connue dans l'Antiquité. La plus ancienne tablette d'argile contenant la valeur correcte, jusqu'à 5 décimales, de √2 = 1,414 21 provient de Babylonie (1800 av. J.-C. - 1600 av. J.-C.). De nombreux autres documents montrent que les racines carrées étaient également utilisées par les anciens Égyptiens, Indiens, Grecs et Chinois. Cependant, l'origine du symbole de la racine √ reste largement spéculative.

• De nombreux chercheurs pensent que les racines carrées proviennent de la lettre « r » : la première lettre du mot latin radix qui signifie racine.
• Une autre théorie affirme que le symbole de la racine carrée a été pris de la lettre arabe ج qui a été placée dans sa forme originale de ﺟ dans le mot جذر - racine (la langue arabe s'écrit de droite à gauche).

La première utilisation du symbole de la racine carrée √ n'incluait pas la « barre » horizontale au-dessus des nombres à l'intérieur du symbole de la racine carrée (ou radical), √‾. La « barre » est connue sous le nom de vinculum en latin, ce qui signifie lien. Bien que le symbole radical avec vinculum soit désormais utilisé dans la vie courante, nous omettons généralement ce surlignage dans de nombreux textes, comme dans les articles sur Internet. La notation des degrés supérieurs d'une racine a été suggérée par Albert Girard, qui a placé l'indice de degré dans l'ouverture du signe radical, par exemple ³√ ou ⁴√.

La dernière question est la suivante : pourquoi l'opération de la racine carrée est-elle appelée racine indépendamment de sa véritable origine ? L'explication devrait devenir plus évidente si nous écrivons l'équation x = ⁿ√a sous une forme différente : xⁿ = a. x est appelé racine ou radical parce qu'il est la base cachée de a. Ainsi, le mot radical ne signifie pas profondeur ou extrême, mais plutôt fondamental, atteignant la racine des choses.

En mathématiques, les opérations traditionnelles sur les nombres sont l'addition, la soustraction, la multiplication et la division. Néanmoins, nous ajoutons parfois à cette liste des opérations et des manipulations plus avancées : racines carrées, exposants, logarithmes et même fonctions trigonométriques (par exemple, sinus et cosinus). Dans cet article, nous nous concentrerons sur la définition de la racine carrée uniquement.

La racine carrée d'un nombre donné x est tout nombre y dont le carré y² = y × y donne le nombre initial x. Par conséquent, la formule de la racine carrée peut être exprimée comme suit :

√x = y ⟺ x = y²

où ⟺ est un symbole mathématique qui signifie si et seulement si. Chaque nombre réel positif a toujours deux racines carrées : la première est positive et la seconde est négative. Cependant, pour de nombreuses utilités pratiques, nous utilisons généralement la racine positive. Le seul nombre qui a une seule racine carrée est zéro. En effet, √0 = 0, et zéro n'est ni positif ni négatif.

Il existe également une autre notation courante des racines carrées qui pourrait s'avérer plus pratique dans de nombreux calculs complexes. Cette formule alternative de la racine carrée stipule que la racine carrée d'un nombre est un nombre élevé à l'exposant de la moitié de la fraction :

√x = x^(1/2) = x^0,5

Dans l'interprétation géométrique, la racine carrée d'une aire donnée d'un carré donne la longueur de son côté. C'est pourquoi √ porte le mot carré dans son nom. Il en va de même pour la racine cubique, ∛. Si vous prenez la racine cubique du volume d'un cuber, vous obtenez la longueur de ses arêtes. Alors que les racines carrées sont utilisées pour étudier les aires, les racines cubiques sont utiles pour déterminer des quantités liées au volume, par exemple la densité.

Nous ne sommes peut-être pas très modestes, mais nous pensons que la meilleure réponse à la question de savoir comment trouver la racine carrée est simple : utiliser le calculateur de racine carrée ! Vous pouvez l'utiliser aussi bien sur votre ordinateur que sur votre smartphone pour estimer rapidement la racine carrée d'un nombre donné. Malheureusement, il y a parfois des situations où vous ne pouvez compter que sur vous-même. Que faire alors ? Pour vous y préparer, vous devez vous souvenir de plusieurs racines carrées parfaites de base :

• Racine carrée de 1 : √1 = 1, puisque 1 × 1 = 1

• Racine carrée de 4 : √4 = 2, puisque 2 × 2 = 4

• Racine carrée de 9 : √9 = 3, puisque 3 × 3 = 9

• Racine carrée de 16 : √16 = 4, puisque 4 × 4 = 16

• Racine carrée de 25 : √25 = 5, puisque 5 × 5 = 25

• Racine carrée de 36 : √36 = 6, puisque 6 × 6 = 36

• Racine carrée de 49 : √49 = 7, puisque 7 × 7 = 49

• Racine carrée de 64 : √64 = 8, puisque 8 × 8 = 64

• Racine carrée de 81 : √81 = 9, car 9 × 9 = 81

• Racine carrée de 100 : √100 = 10, car 10 × 10 = 100

• Racine carrée de 121 : √121 = 11, puisque 11 × 11 = 121

• Racine carrée de 144 : √144 = 12, puisque 12 × 12 = 144

Les nombres entiers ci-dessus sont les racines carrées les plus simples, car on obtient à chaque fois un nombre entier. Essayez de vous en souvenir ! Mais que faire quand il y a un nombre qui n'a pas une racine carrée aussi idéale ? Il existe plusieurs solutions. Tout d'abord, vous pouvez essayer de prédire le résultat par essai et erreur. Disons que vous voulez estimer la racine carrée de 52 :

1. Vous savez que √49 = 7 et √64 = 8, donc √52 devrait être compris entre 7 et 8.

2. Le nombre 52 est plus proche du 49 (donc plus proche du 7), vous pouvez donc essayer de deviner que √52 est 7,3.

3. Ensuite, vous élevez au carré 7,3, obtenant 7,3² = 53,29 (comme l'indique la formule de la racine carrée), ce qui est plus élevé que 52. Vous devez essayer avec un nombre plus petit, disons 7,2.

4. Le carré de 7,2 est 51,84. Vous avez maintenant un nombre plus petit, mais beaucoup plus proche de 52. Si cette précision vous satisfait, vous pouvez arrêter les estimations ici. Sinon, vous pouvez répéter la procédure avec un nombre choisi entre 7,2 et 7,3, par exemple 7,22, et ainsi de suite.

Une autre approche consiste à simplifier d'abord la racine carrée, puis à utiliser les approximations des racines carrées des nombres premiers (généralement arrondies à deux décimales) :

• Racine carrée de 2 : √2 ≈ 1,41
• Racine carrée de 3 : √3 ≈ 1,73
• Racine carrée de 5 : √5 ≈ 2,24
• Racine carrée de 7 : √7 ≈ 2,65
• Racine carrée de 11 : √11 ≈ 3,32
• Racine carrée de 13 : √13 ≈ 3,61
• Racine carrée de 17 : √17 ≈ 4,12
• Racine carrée de 19 : √19 ≈ 4,34

Essayons à nouveau de trouver la racine carrée de 52. Vous pouvez la simplifier en √52 = 2√13 (vous apprendrez à simplifier la racine carrée dans la section suivante), puis la remplacer par √13 ≈ 3,61. Enfin, faites une multiplication √52 ≈ 2 × 3,61 = 7,22. Le résultat est le même que précédemment !

Dans certaines situations, vous n'avez pas besoin de connaître le résultat exact de la racine carrée. Dans ce cas, notre calculateur de racine carrée est la meilleure option pour estimer la valeur de toutes les racines carrées que vous souhaitez. Par exemple, disons que vous voulez savoir si 4√5 est plus grand que 9. Grâce au calculateur, vous savez que √5 ≈ 2,236 07, donc 4√5 ≈ 4 × 2,236 07 = 8,944 28. C'est très proche de 9, mais ce n'est pas plus grand que lui ! Le calculateur de racine carrée donne la valeur finale avec une précision relativement élevée (à cinq chiffres dans l'exemple ci-dessus).

N'oubliez pas que notre calculateur recalcule automatiquement les nombres entrés dans l'un ou l'autre des champs. Vous pouvez trouver la racine carrée d'un nombre spécifique en remplissant le premier champ ou obtenir le carré d'un nombre que vous avez saisi dans le deuxième champ. La seconde option est pratique pour trouver des carrés parfaits qui sont essentiels dans de nombreux aspects des mathématiques et des sciences. Par exemple, si vous entrez 17 dans le deuxième champ, vous découvrirez que 289 est un carré parfait.

Dans certaines applications de la racine carrée, en particulier celles qui concernent les sciences telles que la chimie et la physique, les résultats sont préférés en notation scientifique. En bref, une réponse en notation scientifique doit avoir une virgule décimale entre les deux premiers nombres non nuls. Elle sera représentée comme la décimale multipliée par 10 élevée à un exposant. Par exemple, le nombre 0,003 45 s'écrit 3,45 × 10⁻³ en notation scientifique, tandis que 145,67 s'écrit 1,456 7 × 10² en notation scientifique. Les résultats obtenus en utilisant le calculateur de racine carrée peuvent être convertis en notation scientifique avec le calculateur de notation scientifique.

Tout d'abord, demandons-nous quelles sont les racines carrées qui peuvent être simplifiées. Pour répondre à cette question, vous devez prendre le nombre qui se trouve après le symbole de la racine carrée et trouver ses facteurs. Si l'un de ses facteurs est un nombre au carré (4, 9, 16, 25, 36, 49, 64 et ainsi de suite), vous pouvez simplifier la racine carrée. Pourquoi ces nombres sont-ils élevés au carré ? Ils peuvent être exprimés respectivement par 2², 3², 4², 5², 6², 7² et ainsi de suite. Selon la définition de la racine carrée, vous pouvez les appeler carrés parfaits. Jetons un coup d'œil à quelques exemples.

• Pouvez-vous simplifier √27 ? Les facteurs de 27 sont 1, 3, 9, 27. Il y a 9 ici ! Cela signifie que vous pouvez simplifier √27.

• Pouvez-vous simplifier √15 ? Les facteurs de 15 sont 1, 3, 5 et 15. Il n'y a pas de carrés parfaits dans ces nombres, donc cette racine carrée ne peut pas être simplifiée.

Alors, comment simplifier les racines carrées ? Pour l'expliquer, nous allons utiliser une propriété pratique de la racine carrée dont nous avons parlé précédemment, à savoir la formule alternative de la racine carrée :

√x = x^(1/2)

Nous pouvons utiliser ces deux formes de la racine carrée et passer de l'une à l'autre quand nous le souhaitons. En particulier, nous nous souvenons que la multiplication par une puissance de deux nombres spécifiques est équivalente à la multiplication de ces nombres spécifiques élevés aux mêmes puissances. Par conséquent, nous pouvons écrire :

(x × y)^(1/2) = x^(1/2) × y^(1/2) ⟺ √(x × y) = √x × √y

Comment pouvez-vous utiliser ces connaissances ? L'argument d'une racine carrée n'est généralement pas un carré parfait que vous pouvez facilement calculer, mais il peut contenir un carré parfait parmi ses facteurs. En d'autres termes, vous pouvez l'écrire comme une multiplication de deux nombres, où l'un des nombres est le carré parfait, par exemple 45 = 9 × 5 (9 est un carré parfait). L'exigence d'avoir au moins un facteur qui est un carré parfait est nécessaire pour simplifier la racine carrée. À ce stade, vous devriez probablement savoir quelle sera la prochaine étape. Vous devez placer cette multiplication sous la racine carrée. Dans notre exemple :

√45 = 45^(1/2) = (9 × 5)^(1/2) = 9^(1/2) × 5^(1/2) = √9 × √5 = 3√5

Vous avez réussi à simplifier votre première racine carrée ! Bien sûr, vous n'avez pas besoin d'écrire tous ces calculs. Tant que vous vous souvenez que la racine carrée est équivalente à la puissance d'un demi, vous pouvez les abréger. Entraînons-nous à simplifier les racines carrées avec d'autres exemples.

• Comment simplifier la racine carrée de 27 ?

  √27 = √(9 × 3) = √9 × √3 = 3√3

• Comment simplifier la racine carrée de 8 ?

  √8 = √(4 × 2) = √4 × √2 = 2√2

• Comment simplifier la racine carrée de 144 ?

  √144 = √(4 × 36) = √4 × √36 = 2 × 6 = 12

Dans le dernier exemple, vous n'avez pas eu à simplifier du tout la racine carrée, car 144 est un carré parfait. Vous pouvez simplement vous rappeler que 12 × 12 = 144. Cependant, nous voulions vous montrer qu'avec le processus de simplification, vous pouvez facilement calculer les racines carrées des carrés parfaits également. C'est utile lorsqu'il s'agit de grands nombres.

Enfin, vous vous demandez peut-être comment simplifier les racines d'ordre supérieur, par exemple les racines cubiques 🇺🇸. En fait, le processus est très analogue à celui des racines carrées, mais dans le cas des racines cubiques, vous devez trouver au moins un facteur qui est un cube parfait, et non un carré parfait, c'est-à-dire 8 = 2³, 27 = 3³, 64 = 4³, 125 = 5³ et ainsi de suite. Ensuite, vous divisez votre nombre en deux parties et vous les placez sous la racine cubique. Prenons l'exemple suivant de simplification de ³√192 :

∛192 = ∛(64 × 3) = ∛64 × ∛3 = 4∛3

Cela peut sembler un peu compliqué au premier coup d'œil, mais après un peu de pratique, vous serez capable de simplifier les racines dans votre tête. Faites-nous confiance !

Addition de racines carrées et soustraction de racines carrées

Malheureusement, l'addition ou la soustraction de racines carrées n'est pas aussi facile que l'addition/soustraction de nombres ordinaires. Par exemple, si 2 + 3 = 5, cela ne signifie pas que √2 + √3 est égal à √5. Pour comprendre pourquoi, imaginez que vous avez deux types de formes différentes : des triangles 🔺 et des cercles 🔵. Que se passe-t-il lorsque vous ajoutez un triangle à un cercle 🔺 + 🔵 ? Rien du tout ! Vous avez toujours un triangle et un cercle 🔺 + 🔵. À maints égards, que se passe-t-il lorsque vous essayez d'ajouter trois triangles à cinq triangles : 3🔺 + 5🔺 ? Vous obtiendrez huit triangles 8🔺.

L'addition de racines carrées est très similaire à celle-ci. Le résultat de l'addition de √2 + √3 est toujours √2 + √3. Vous ne pouvez pas le simplifier davantage. La situation est toutefois différente lorsque les deux racines carrées ont le même nombre sous le symbole de la racine. On peut alors les additionner comme des nombres normaux (ou des triangles). Par exemple, 3√2 + 5√2 égalent 8√2. Il en va de même pour la soustraction de racines carrées. Jetons un coup d'œil à d'autres exemples illustrant cette propriété des racines carrées :

• Que représente 6√17 + 5√17 ?

  Réponse : 6√17 + 5√17 = 11√17

• Que représente 4√7 - 7√7 ?

  Réponse : 4√7 - 7√7 = -3√7

• Que représente 2√2 + 3√8 ?

  Réponse : 2√2 + 3√8 = 2√2 + 6√2 = 8√2, car on a simplifié √8 = √(4 × 2) = √4 × √2 = 2√2.

• Quelle est la valeur de √45 - √20 ?

  Réponse : √45 - √20 = 3√5 - 2√5 = √5, car nous avons simplifié √45 = √(9 × 5) = √9 × √5 = 3√5 et √20 = √(4 × 5) = √4 × √5 = 2√5.

• Quelle est la valeur de 7√13 + 2√22 ?

  Réponse : 7√13 + 2√22 (nous ne pouvons pas simplifier davantage)

• Que représente √3 - √18 ?

  Réponse : √3 - √18 = √3 - 3√2, nous ne pouvons pas simplifier davantage, mais nous avons au moins simplifié √18 = √(9 × 2) = √9 × √2 = 3√2.

Multiplier les racines carrées et diviser les racines carrées

Maintenant que l'addition des racines carrées est un jeu d'enfant pour vous, allons plus loin. Qu'en est-il de la multiplication des racines carrées et de la division des racines carrées ? N'ayez pas peur ! En fait, vous l'avez déjà fait lors de la leçon sur la simplification des racines carrées. Multiplier des racines carrées est basé sur la propriété de la racine carrée que nous avons déjà utilisée à plusieurs reprises, à savoir :

√x = x^(1/2)

Vous souvenez-vous de la façon de multiplier des nombres élevés à la même puissance ? Pour rappel :

xⁿ × yⁿ = (x × y)ⁿ

et donc,

x^(1/2) × y^(1/2) = (x × y)^(1/2) ⟺ √x × √y = √(x × y)

Contrairement à l'addition, vous pouvez multiplier deux racines carrées. Rappelez-vous que la multiplication possède des propriétés commutatives, ce qui signifie que l'ordre dans lequel deux nombres sont multipliés n'a pas d'importance. Quelques exemples devraient vous éclairer sur ce point.

• Qu'est-ce que √3 × √2 ?
  Réponse : √3 × √2 = √6

• Que représente 2√5 × 5√3 ?

  Réponse : 2√5 × 5√3 = 2 × 5 × √5 × √3 = 10√15, car la multiplication est commutative.

• Que représente 2√6 × 3√3 ?

  Réponse : 2√6 × 3√3 = 2 × 3 × √6 × √3 = 6√18 = 18√2, on a simplifié √18 = √(9 × 2) = √9 × √2 = 3√2.

Diviser une racine carrée revient presque au même puisque :

x^(1/2) / y^(1/2) = (x / y)^(1/2) ⟺ √x / √y = √(x / y)

Il suffit de remplacer le signe de la multiplication par celui d'une division. Cependant, la division n'est pas une opération commutative ! Vous devez calculer séparément les nombres qui se trouvent avant les racines carrées et les nombres qui se trouvent sous les racines carrées. Comme toujours, voici quelques exemples pratiques :

• Que représente √15 / √3 ?

  Réponse : √15 / √3 = √5

• Quelle est la valeur de 10√6 / 5√2 ?

  Réponse : 10√6 / 5√2 = (10 / 5) × (√6 / √2) = 2√3

• Quelle est la valeur de 6√2 / 3√5 ?

  Réponse : 6√2 / 3√5 = (6 / 3) × (√2 / √5) = 2√(2/5) = 2√(0,4), on est passé d'une fraction simple 2/5 à une fraction décimale 2/5 = 4/10 = 0,4.

Calculer la racine carrée de nombres élevés à une puissance ou la racine carrée de fractions n'est peut-être pas évident pour vous. Mais avec les connaissances que vous avez acquises dans la section précédente, vous devriez trouver cela plus facile que vous ne le pensiez ! Commençons par les racines carrées des puissances. Dans ce cas, il vous sera plus facile d'utiliser la forme alternative de la racine carrée √x = x^(1/2). Vous souvenez-vous de la règle des puissances ? Si ce n'est pas le cas, voici un petit rappel :

(xⁿ)^m = x^{(n × m)}

où, n et m sont des nombres réels quelconques. Or, si vous placez 1/2 à la place de m, vous n'obtiendrez rien d'autre qu'une fraction comme exposant :

√(xⁿ) = (xⁿ)^(1/2) = x^(n/2)

Voilà comment trouver la racine carrée d'un nombre élevé à une puissance. En parlant de puissance, l'équation ci-dessus ressemble beaucoup à la fonction de densité de la loi normale centrée réduite, qui est largement utilisée dans les statistiques.

Si vous n'êtes toujours pas sûr·e de pouvoir prendre la racine carrée d'une puissance, voici quelques exemples :

• Racine carrée de 2⁴ :

  √(2⁴) = (2⁴)^(1/2) = 2^(4/2) = 2² = 4

• Racine carrée de 5³ :

  √(5³) = (5³)^(1/2) = 5^(3/2)

• Racine carrée de 4⁵ :

  √(4⁵) = (4⁵)^(1/2) = 4^(5/2) = (2²)^(5/2) = 2⁵ = 32

Comme vous pouvez le constater, il est parfois impossible d'obtenir un joli résultat comme dans le premier exemple. Cependant, dans le troisième exemple, nous vous avons montré une petite astuce en exprimant 4 par 2². Cette approche permet souvent de simplifier des équations plus compliquées.

Qu'en est-il des racines carrées des fractions ? Jetez un coup d'œil à la section précédente où nous avons parlé de la division des racines carrées. Vous y trouverez la relation suivante qui devrait tout expliquer :

(x / y)^(1/2) ⟺ √x / √y = √(x / y)

où x / y est une fraction. Vous trouverez ci-dessous quelques exemples de racines carrées d'une fraction :

• Racine carrée de 4/9 :

  √(4/9) = √4 / √9 = 2/3

• Racine carrée de 1/100 :

  √(1/100) = √1 / √100 = 1/10

• Racine carrée de 1/5 :

  √(1/5) = √1 / √5 = 1/√5 = √5/5

Laisser des racines au dénominateur n'est pas une très bonne habitude. C'est pourquoi nous nous en sommes débarrassées dans le dernier exemple. Nous avons simplement multiplié le numérateur et le dénominateur par le même nombre (on peut toujours faire cela, car le nombre par lequel on multiplie est égal à 1), dans ce cas, par √5.

Les fonctions jouent un rôle essentiel non seulement en mathématiques, mais aussi dans de nombreuses autres aires telles que la physique, les statistiques ou la finance. La fonction f(x) n'est rien d'autre qu'une formule qui indique comment la valeur de f(x) change en fonction de l'argument x. Vous trouverez ici des fonctions que vous pouvez appliquer dans la vie réelle. Elles vous seront d'une grande aide si vous voulez savoir comment calculer des intérêts composés ou estimer la valeur future d'une rente.

Vous trouverez ci-dessous le graphique de la racine carrée, constitué de la moitié d'une parabole. Vérifiez-le et essayez de valider, par exemple, si la fonction racine carrée de x = 9 est 3 et de x = 16 est 4 (comme elle devrait l'être).

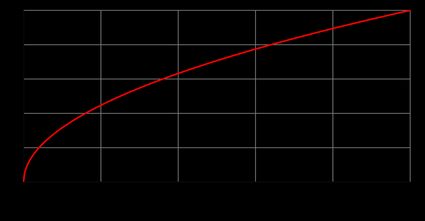
Revenons à la fonction racine carrée f(x) = √x et explorons ses propriétés de base. Nous ne considérons ici que la partie positive de f(x) (comme vous pouvez le voir sur le graphique de la racine carrée ci-dessus). Donc, la fonction racine carrée :

• est continue et croissante pour tout x non négatif ;

• est dérivable pour tous les x positifs (voir la section sur la dérivée de la racine carrée pour plus d'informations) ;

• tend ver l'infini lorsque x s'approche de l'infini (lim √x → ∞ lorsque x → ∞) ; et

• est un nombre réel pour tous les x non négatifs et un nombre complexe pour tous les x négatifs.

La dérivée d'une fonction nous indique à quelle vitesse cette fonction change en fonction de son argument. L'un des exemples les plus simples en physique est la position d'un objet et sa vélocité (le taux de variation de la position). Disons que la fonction x(t) décrit comment la distance d'une voiture en mouvement par rapport à un point spécifique change en fonction du temps t. Savez-vous ce qui détermine la vitesse de variation de la distance parcourue ? La réponse est la vitesse de la voiture ! Ainsi, la dérivée de la position x(t) est la vitesse v(t) (la vitesse peut également dépendre du temps). Pour désigner la dérivée, on utilise généralement l'apostrophe v(t) = x'(t) ou le symbole de la dérivée v(t) = dx(t)/dt.

La dérivée de la fonction générale f(x) n'est pas toujours facile à calculer. Cependant, dans certaines circonstances, si la fonction prend une forme spécifique, on dispose de quelques formules. Par exemple, si :

f(x) = xⁿ

où n est un nombre réel quelconque, la dérivée est la suivante :

f'(x) = n × x^(n-1)

Cela n'en a peut-être pas l'air, mais cela répond à la question de savoir à quoi ressemble la dérivée d'une racine carrée. Vous souvenez-vous de la forme alternative (exponentielle) d'une racine carrée ? Laissez-nous vous le rappeler :

√x = x^(1/2)

Vous voyez que dans ce cas, n = 1/2, donc la dérivée d'une racine carrée est :

(√x)' = (x^(1/2))' = 1/2 × x^(-1/2) = 1/(2√x)

Étant donné qu'un nombre à une puissance négative est égal à 1 sur ce nombre, l'estimation de la dérivée fera intervenir des fractions. Nous avons un outil qui pourrait être essentiel lors de l'addition ou de la soustraction de fractions avec des dénominateurs différents. Il s'agit du calculateur PPCM, qui vous indique comment trouver le plus petit commun multiple.

La dérivée d'une racine carrée est nécessaire pour obtenir les coefficients des séries de Taylor. Nous ne voulons pas aller trop loin dans les détails, donc brièvement, les séries de Taylor vous permettent d'approximer diverses fonctions avec les polynômes qui sont beaucoup plus faciles à calculer. Par exemple, la série de Taylor de √(1 + x) autour du point x = 0 est donné par :

√(1 + x) = 1 + 1/2 × x - 1/8 × x² + 1/16 × x³ - 5/128 × x⁴ + ... (valable pour -1 ≤ x ≤ 1)

Bien que l'expression ci-dessus ait un nombre infini de termes, pour obtenir la valeur approximative, vous pouvez utiliser seulement les quelques premiers termes. Essayez donc ! Avec x = 0,5 et les cinq premiers termes, vous obtenez :

√(1,5) = 1 + 1/2 × 0,5 - 1/8 × 0,25 + 1/16 × 0,125 - 5/128 × 0,062 5

√(1,5) ≈ 1,224 1

La valeur réelle, fournie par notre calculateur, est √(1,5) ≈ 1,224 7. C'est assez proche !

Cela fait beaucoup de mathématiques et d'équations jusqu'à présent. Pour ceux d'entre vous qui sont suffisamment persévérants, nous avons préparé la section suivante, qui explique comment calculer la racine carrée d'un nombre négatif.

À l'école, on vous a probablement appris que la racine carrée d'un nombre négatif n'existe pas. C'est vrai si vous ne considérez que les nombres réels. Il y a longtemps, pour effectuer des calculs avancés, les mathématiciens ont dû introduire un ensemble plus général de nombres : les nombres complexes. Ils peuvent être exprimés sous la forme suivante  

x = a + b × i

où, x est le nombre complexe avec la partie réelle a et la partie imaginaire b. Ce qui différencie un nombre complexe d'un nombre réel est le nombre imaginaire i. Voici quelques exemples de nombres complexes : 2 + 3i, 5i, 1,5 + 4i, et 2. Vous serez peut-être surpris·e de voir 2, qui est un nombre réel. Oui, c'est vrai, mais c'est aussi un nombre complexe avec b = 0. Les nombres complexes sont une généralisation des nombres réels.

Jusqu'à présent, le nombre imaginaire i est probablement encore un mystère pour vous. De quoi s'agit-il en fait ? Eh bien, bien qu'il puisse sembler bizarre, il est défini par l'équation suivante :

i = √(-1)

C'est tout ce dont vous avez besoin pour calculer la racine carrée de n'importe quel nombre, qu'il soit positif ou non. Voyons quelques exemples :

• Racine carrée de -9 : √(-9) = √(-1 × 9) = √(-1)√9 = 3i
• Racine carrée de -13 : √(-13) = √(-1 × 13) = √(-1)√13 = i√13
• Racine carrée de -49 : √(-49) = √(-1 × 49) = √(-1)√49 = 7i

Simple, n'est-ce pas ? Ce problème ne se pose pas avec la racine cubique puisque vous pouvez obtenir le nombre négatif en multipliant trois des nombres négatifs identiques (ce que vous ne pouvez pas faire avec deux nombres négatifs). Par exemple :

³√(-64) = ³√[(-4)×(-4)×(-4)] = -4

C'est tout ce que vous devez savoir sur les racines carrées !